Простейшие модели управления запасами характеризуются постоянным по времени спросом, мгновенным пополнением запаса и отсутствием дефицита. Введём обозначения:

y - объём заказа (количество единиц продукции)

D - интенсивность спроса (измеряется в единицах продукции на единицу времени)

t ₀ - продолжительность цикла заказа (измеряется во временных единицах)

Уровень запаса изменяется в соответствии с функцией:

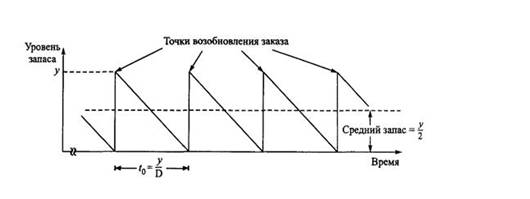
Средний уровень запаса определяется соотношением y /2.

Объём заказа y единиц размещается и пополняется мгновенно, когда уровень запаса равен нулю. Затем запас равномерно расходуется с постоянной интенсивностью спроса D. Продолжительность цикла заказа для этого примера равна (в единицах времени):

t ₀ = y / D

Для построения функции затрат требуется два стоимостных параметра.

K - затраты на оформление, связанные с размещением заказа,

h - затраты на хранение (затраты на единицу складируемой продукции в единицу времени).

Суммарные затраты в единицу времени (обозначаются TCU) можно представить как функцию от y в виде суммы затрат на оформление заказа в единицу времени и затрат на хранение запаса в единицу времени, т. е. отношение суммы затрат на оформление и хранение ко времени.

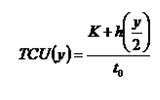
Подставив t ₀ = y / D , мы получаем:

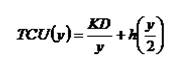
Оптимальное значение объёма заказа определяется путём минимизации по y функции TCU ( y ). Предполагая, что y является непрерывной переменной, получаем необходимое условие минимума, из которого можно найти оптимальное значение y:

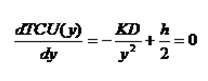
Это условие является также и достаточным, так как функция выпуклая. Решение данного уравнения определяет экономический объём заказа y’:

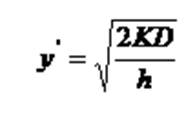
Оптимальная стратегия управления запасами для рассмотренной модели формулируется следующим образом.

Заказывать 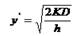   единиц продукции через каждые  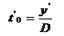единиц времени.

В действительности пополнение запаса не может производиться мгновенно в момент размещения заказа, как предполагалось ранее. Для большинства реальных ситуаций существует положительный срок выполнения заказа L (временное запаздывание) от момента его размещения до реальной поставки:

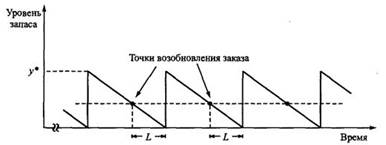
В этом случае точка возобновления запаса имеет место, когда уровень запаса опускается до LD единиц.

На этом рисунке представлено изменение уровня запаса во времени при условии, что срок выполнения заказа меньше продолжительности цикла заказа, что в общем случае выполняется не всегда. В противном случае определяется эффективный срок L ₀ выполнения заказа в виде

L ₀ = L – nt ₀ ’

где n - наибольшее целое, не превышающее L / t ₀ ’