Доминирующей чистой стратегией игроков А и В в биматричной игре с матрицами выигрышей называется стратегия, соответствующие элементы которой больше соответствующих элементов другой чистой стратегии, называемой доминируемой (в матрице затрат наоборот).
Пример: Требуется редуцировать размерность задачи за счет исключения заведомо невыгодных стратегий следующих матриц выигрышей биматричной игры:

Решение. Рассмотрим первый критерий задачи: сторона А хочет максимизировать свой выигрыш. По этому критерию из матрицы А удаляются доминируемые строки. При сравнении выигрышей в стратегиях A2 и A4 видно, что все элементы четвертой строки больше соответствующих элементов второй строки, следовательно, из матрицы А удаляется вторая строка. Автоматически удаляется вторая строка и из матрицы В. Таким образом, после отработки первого критерия матрицы выигрышей выглядят следующим образом: 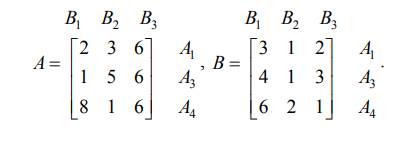
Перейдем к рассмотрению второго критерия – сторона А хочет минимизировать выигрыш стороны В. По данному критерию из матрицы удаляются доминирующие строки. Строка, соответствующая стратегии A3 , является доминирующей по отношению к строке, соответствующей стратегии A1 , и удаляется из матрицы В. Из матрицы А также удаляется строка, соответствующая стратегии A3 . Таким образом, после применения отношений доминирования матрицы выигрышей принимают следующий вид:
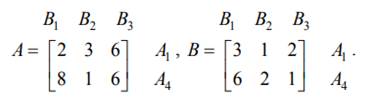
Сторона В хочет минимизировать выигрыш стороны А. По данному критерию из матрицы А удаляются доминирующие столбцы. Столбец B3 является доминирующим по отношению к столбцу B2 и удаляется из матрицы. Соответственно, из матрицы В также удаляется третий столбец. Таким образом, после применения отношений доминирования матрицы выигрышей принимают следующий вид:
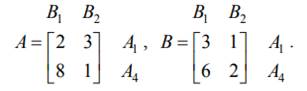
15. Позиционные игры – основные определения.
Позиционной игрой называется бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени информации.
Простейшие примеры позиционных игр: шахматы, шашки, крестики-нолики, домино.
Игра в позиционной форме представляется деревом игры – графом, вершины которого соответствуют состояниям игры (позициям), а ребра, выходящие из вершин, отображают варианты выбора решений в этих позициях.
Если при выполнении очередного хода игрок не знает всей предыстории игры, т.е. всех выборов ходах, то он фактически не знает в какой позиции осуществляется его выбор на данном ходе. Такие игры называются играми с неполной информацией.
Если каждое информационное множество игры содержит только одну позицию, то получаем игру с полной информацией, в которой каждый игрок на любом шаге знает всю предысторию процесса игры.
Для описания неопределенности, с которой сталкивается игрок на своем ходе, используется разбиение множества на подмножества, называемые информационными множествами, и принимается, что позиции, принадлежащие одному информационному множеству, для него неразличимы на предыдущих.
Дата: 2019-03-05, просмотров: 902.