Пример 3.4. На отрезке [1, 3] решить дифференциальное уравнение первого порядка y' = 2,5x + cos(y + 0,6) с начальным условием у(1) = 1,5 с шагом 0,2.
MathCAD
При решении задач Коши для обыкновенных дифференциальных уравнении методом Рунге-Кутта с переменным шагом в MathCAD пользуются вычислительным блоком Given/Odesolve. Он состоит из трех частей:
1. ключевое слово Given;
2. уравнение и начальные условия, записанные с помощью логических операторов;
3. вызов встроенной функции Odesolve(x, x1) дадя. решения, уравнения на интервале (x0,x1).
Допустимо задание функции в виде Odesolve(x, x1, step), где step-, внутренний параметр численного метода, определяющий количество шагов, в которых метод Рунге-Кутта будет вычислять решение. Чем больше step, тем с лучшей точностью будет получен результат, нотем больше времени будет затрачено на его поиск. Подбором этого параметра можно в несколько раз ускорить расчеты без существенного ухудшения точности решения.
Решение (распечатка MathCAD)
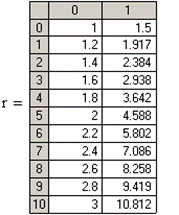
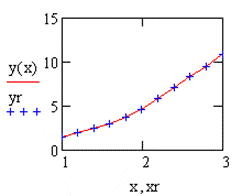
Решение в среде MathCAD с помощью функции rkfixed методом Рунге-Кутта четвёртого порядка:
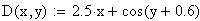
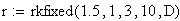
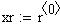
Решение в среде MathCAD с помощью функции Odesolve:
Given
у' (х) = 2.5 -х + cos(y (х) + 0.6)
у(1)=1.5
y:=Odesolve(x,3)
SMath Studio
При решении задач Коши для обыкновенных дифференциальных уравнений методом Рунге-Кутта с фиксированным шагом в SMath Studio используется функция rkfixed. Правая часть дифференциального уравнения записывается как функция D(x;y). Кроме этого, задаются: шаг, границы интервала решения, начальное значение функции y(x) на левой границе интервала, и вычисляется количество точек на интервале.
Решение (распечатка SMath Studio)
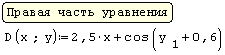
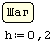Границы интервала
 
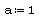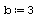
| Примечание: Если в правой части сама функция y встречается внутри функций sin, cos, tg, ln и т.п., ее нужно написать с индексом 1 (единица), т.е. вместо y должно быть написано y 1. Это можно сделать с помощью шаблона  «Элемент вектора» с панели Матрицы.
|
Начальное значение функции
| 
|
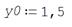
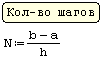
Примечание: Для выполнения задания необходимо, чтобы в SMathStudio было установлено дополнение «ODE Solvers». Наличие дополнения можно проверить в менеджере расширений SMathStudio, открыв его через главное меню программы: Сервис – Дополнения… . Если дополнение отсутствует, его можно установить при наличии подключения к Интернету, сменив «Локальное хранилище» на «Галерею онлайн» в окне менеджера расширений.
Нахождение уравнения линейной регрессии
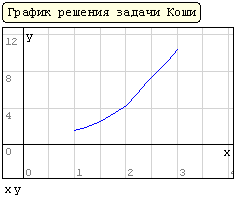
Пример 3.5. Построить линейную регрессию для функции, заданной таблицей (табл. 8).
MathCAD
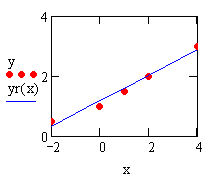
Для реализации линейной регрессии в системе MathCAD имеется функция line(x,y), которая выдает вектор из двух элементов (а, b) линейной регрессии a+b х; где x – вектор значений аргумента; у – вектор значений функции.
Решение (распечатка MathCAD)
 
| 
| 
|
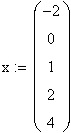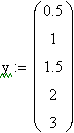
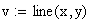
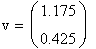
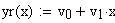
SMath Studio
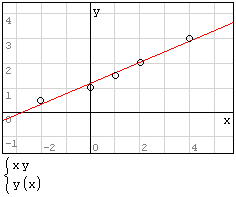
Для реализации линейной регрессии в системе SMath Studio используются функции Slope и Intercept, которые дают значения коэффициента наклона прямой и сдвига по оси ординат, соответственно. Данные по х и по у нужно задать в виде матриц-столбцов. Кроме того, нужно задать дополнительный столбец из латинских букв "o" в кавычках для наглядного построения данных в виде точек.
Решение (распечатка SMath Studio)
  
| 
|
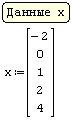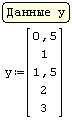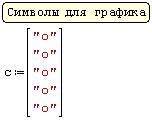
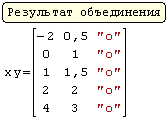
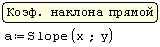
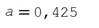
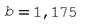
Примечание: Для выполнения задания необходимо, чтобы в SMathStudio было установлено дополнение «Statistical Tools». Как установить дополнение, см. в примечании к предыдущему примеру.
Заключение
Выполнение контрольной работы позволит студентам освоить численные методы решения тех задач, которые встречаются в их профессиональной сфере. Краткая теоретическая часть позволит студентам глубже понять теоретические основы используемых численных методов, а применение пакетов программ сделает решение профессиональных задач более эффективным.
Библиографический список
1 Кирьянов, Д.В. Самоучитель MathCAD 2001 [Текст] : самоучитель / Д. В. Кирьянов.- СПб. : БХВ-Петербург, 2002. - 544 с
2 Бахвалов, Н.С. Численные методы [Текст] : учеб. пособие для ВУЗов / Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков.- М. : БИНОМ, 2006. - 636 с.
3 Голубева, Н.В. Математическое моделирование систем и процессов [Текст] : учеб. пособие для ВУЗов ж.-д. трансп. / Н. В. Голубева.- СПб.: Лань, 2013. - 192 с.
4 Белобородова, Т.В. Математическое моделирование в среде MathCAD [Текст] : учебное пособие / Т. В. Белобородова.- Красноярск: КФ ИрГУПС, 2003. - 366 с.
5 Бояркина, Галина Петровна. Математическое моделирование систем и процессов [Электронный ресурс]: учеб. пособие. Часть 1: Численные методы, 2011. - 160 с. on-line
6 Багдуева, Ханда Нимаевна. Математическое моделирование систем и процессов [Электронный ресурс]: учеб. пособие. Часть 2: Моделирование динамических систем, 2011. - 144 с.
7 Менакер, К.В. Математическое моделирование систем и процессов [Электронный ресурс]: методические указания по выполнению контрольной работы для студентов 2 курса заочной формы обучения специальности 23.05.05 "Системы обеспечения движения поездов" всех специализаций / К. В. Менакер, М. А. Павленко.- Чита: ЗабИЖТ, 2014. -15 с.
8 Маничев, В.Б. Численные методы. Достоверное и точное численное решение дифференциальных и алгебраических уравнений в CAE-системах САП [Электронный ресурс]: учебное пособие / В. Б. Маничев, В. В. Глазкова, И. А. Кузьмина.- М.: ИНФРА-М, 2016.
9 Безруков, А.И. Математическое и имитационное моделирование [Электронный ресурс]: учебное пособие / А. И. Безруков, О. Н. Алексенцева.- М. : ФОРУМ : ИНФРА-М, 2017. - 227 с.
10 Положение «Требования к оформлению текстовой и графической документации. Нормоконтроль» [Электронный ресурс]: принято решением Ученого Совета 27.01.2012г., протокол № 6; Утв. приказом ректора 06.03.2012г., № 63 (изд. апрель 2017 г.).- Иркутск: ИрГУПС, 2017. - 46 с.
Практикум по выполнению контрольной работы
Белобородова Татьяна Викторовна
Новиков Павел Вадимович
Дата: 2019-03-05, просмотров: 531.
