Данные, с которыми приходится иметь дело инженеру, часто представляются в виде таблиц. Таким образом, функция у = f(x) задается не аналитическим выражением, а в виде пар чисел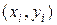 
, 
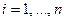. Обычно так представляются результаты экспериментов, обработка статистических наблюдений и т.д. Поэтому встает задача аппроксимации дискретной зависимости
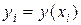
непрерывной функцией
,
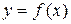т.е. задача построения математической модели функции по ее известным значениям.
В зависимости от специфики задачи функция f(х) может отвечать различным требованиям (рис. 4):
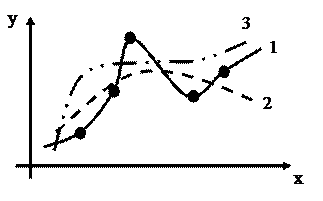
Рис. 4
1. Функция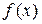 
должна проходить через точки 
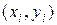т.е.
.
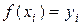В этом случае говорят об интерполяции данных функции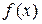 
во внутренних точках между 
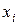и об экстраполяции ее за пределами интервала, содержащего все .
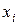2. Функция 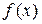должна приближать 
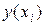, не обязательно проходя через точки 
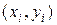, сглаживая экспериментальную зависимость. Это задача регрессии.
3. 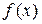должна приближать 
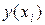, учитывая, что данные 
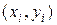получены с некоторой погрешностью, выражающей шумовую компоненту измерений. Задачи такого типа называют задачами фильтрации.
В задачах регрессии данные приближаются некоторой функцией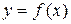 
таким образом, чтобы минимизировать совокупность ошибок 
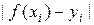. Тогда задача нахождения эмпирической функции 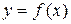разбивается на 2 этапа:
1. установить вид зависимости 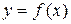, т.е. решить, является ли она линейной, квадратичной, логарифмической и т.п.;
2. определить неизвестные параметры функции 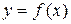. Чаще всего параметры функции определяют по методу наименьших квадратов.
Обозначим
, 
.
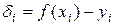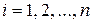Величины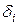 
называют невязками или отклонениями теоретических значений 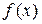от соответствующих экспериментальных значений 
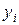(рис. 5).
В методе наименьших квадратов в качестве неизвестных параметров функции 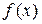выбирают такие, чтобы сумма квадратов невязок была минимальной, т.е.
.
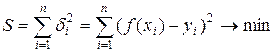Возьмем, например, в качестве функции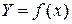 
линейную функцию
.
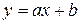Задача сводится к отысканию значений параметров а и дающих минимум функции
.
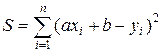Такая функция является функцией двух переменных а и b, т.к. значения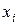 
и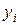 
– постоянные числа.
Для того чтобы найти минимум такой функции нужно приравнять к нулю ее частные производные, т.е.
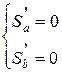или 
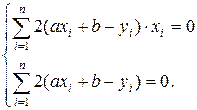(20)
Преобразуем систему (20):
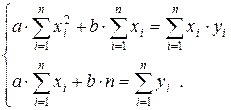(21)
Эта система называется системой нормальных уравнений.
После ее решения определяются параметры а и b. Можно доказать, что в точках а и b функция S имеет минимум.
Аналогичным образом можно получить уравнения для определения коэффициентов при других типах функций.
Пример 2.5. Методом наименьших квадратов найти эмпирическую формулу 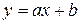для функции, заданной таблицей (табл. 8).
Таблица 8
| x | -2 | 0 | 1 | 2 | 4 |
| y | 0,5 | 1 | 1,5 | 2 | 3 |
Решение
Сведем все вычисления, необходимые для составления
нормальной системы уравнений (21), в таблицу (табл. 9).
Таблица 9
|
|
| 
| 
| |
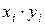
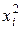
| –2 | 0,5 | –1 | 4 | |
| 0 | 1 | 0 | 0 | |
| 1 | 1,5 | 1,5 | 1 | |
| 2 | 2 | 4 | 4 | |
| 4 | 3 | 12 | 16 | |
| Σ | 5 | 8 | 16,5 | 25 |
Тогда система нормальных уравнений (21) имеет вид
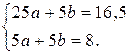
Отсюда
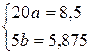
или
; 
.
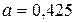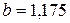Получаем зависимость
y = 0,425х + 1,175.
Для сравнения полученной зависимости и исходных данных
можно составить таблицу
Таблица 10
| x | –2 | 0 | 1 | 2 | 4 |
| y | 0,5 | 1 | 1,5 | 2 | 3 |
| 0,425x+1,175 | 0,325 | 1,175 | 1,6 | 2,025 | 2,875 |
| δ | –0,175 | 0,175 | 0,1 | 0,025 | –0,125 |
Также для сравнения можно построить график, где исходные данные отобразить точками, а полученную зависимость – линией (рис. 6).
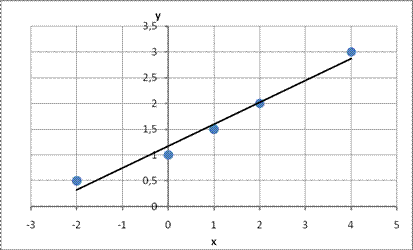
Рис. 6
Дата: 2019-03-05, просмотров: 340.
