Многие задачи механики, физики, химии и других отраслей науки и техники при их математическом моделировании сводятся к дифференциальным уравнениям. В связи с этим решение дифференциальных уравнений является одной из важнейших математических задач.

Постановка задачи

Рассмотрим задачу Коши для дифференциального уравнения 1-го порядка

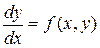                                                        (17)

с начальным условием

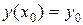              .                                       (18)

Требуется найти функцию 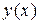, удовлетворяющую уравнению (17) и начальному условию (18).

Хотя решение некоторых задач Коши может быть найдено аналитически, во многих случаях, в том числе для большинства задач, представляющих практический интерес, такой путь часто оказывается невозможным, например, коэффициенты или функции в дифференциальном уравнении могут содержать нелинейности или задаваться в виде таблиц экспериментальных данных. В этом случае пользуются приближенным методам решения задач Коши.

Выделяют два класса приближенных методов решения задач (17), (18): одношаговые и многошаговые. Первый класс методов требует для нахождения следующего значения неизвестной функции 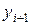 значение только в одной текущей точке 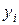, т.е.

              ,    
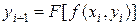а второй класс – в нескольких, например,

              .

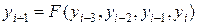Методы второго класса поэтому не обладают свойством «самостартования», т.е. ими нельзя начать решение задачи Коши, оно всегда начинается одношаговыми методами. К достоинствам многошаговых методов относят в основном меньший объем памяти компьютера, требующейся для их реализации, и возможность теоретической оценки погрешности решения. Представителем класса многошаговых методов являются методы прогноза и коррекции. К классу одношаговых методов относятся методы Эйлера, Рунге-Кута и др. Как и во многих других случаях, эти два класса методов лучше сочетать, учитывая их достоинства и недостатки.

Метод Рунге-Кутта

Идея метода Рунге-Кутта состоит в представлении разности

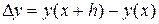
в виде суммы поправок 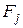 с коэффициентами :

              ,     

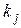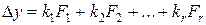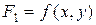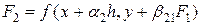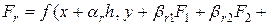
где , , …, 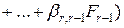. Коэффициенты  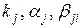находятся сравнением разложения  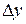и 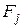, по степеням h.

В сущности, этот метод объединяет целое семейство методов решения дифференциальных уравнений первого порядка (метод Эйлера, модифицированный метод Эйлера и др.). Наиболее распространенным из них является метод четвертого порядка точности для r = 4, ошибка при этом имеет порядок. Этот метод часто и называют методом Рунге-Кутта. Расчеты в нем проводятся по формулам

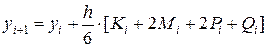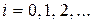,       (19)
где

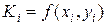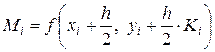, ,         (19a)

, .

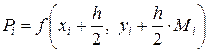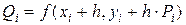Пример 2.4. Решить уравнение

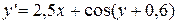
с начальным условием

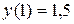
на отрезке [1; 3] с шагом .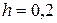

Решение

Имеем 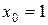, 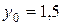. Используя формулу (19) для нахождения значений K_i, M_i, P_i, Q_i получим значения 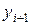. Для удобства сведем все вычисления в таблицу (табл. 7).

                                                              Таблица 7

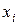
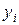
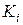
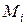
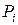
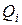
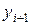
1	1,5	1,995	2,084	2,077	2,19	1,917
1,2	1,917	2,189	2,331	2,326	2,513	2,384
1,4	2,384	2,512	2,754	2,757	3,077	2,938
1,6	2,938	3,078	3,488	3,515	4,046	3,642
1,8	3,642	4,047	4,684	4,748	5,461	4,588
2	4,588	5,458	6,103	6,135	6,491	5,802
2,2	5,802	6,493	6,469	6,471	6,157	7,086
2,4	7,086	6,167	5,816	5,848	5,658	8,258
2,6	8,258	5,656	5,75	5,75	6,165	9,419
2,8	9,419	6,171	6,898	6,967	7,905	10,813
3	10,813