С задачей решения систем линейных алгебраических уравнений (СЛАУ) при моделировании приходится сталкиваться чаще всего. Это неудивительно, т.к. математические модели тех или иных явлений или процессов либо сразу строятся как линейные алгебраические, либо сводятся к таковым посредством дискретизации или линеаризации.
Постановка задачи
В общем случае система линейных алгебраических уравнений
имеет вид
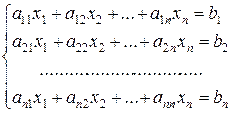 (6)
(6)
Требуется найти неизвестные 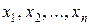 , удовлетворяющие системе уравнений (6).
, удовлетворяющие системе уравнений (6).
В матричной форме СЛАУ (6) записывается в виде
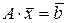 ,
,
где
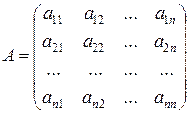 ;
- вещественная матрица данной системы (6); ;
- вещественная матрица данной системы (6);
| 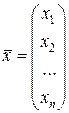 ;
- вектор неизвестных; ;
- вектор неизвестных;
|  ;
- вектор свободных членов. ;
- вектор свободных членов.
|
Матрица А системы (6) является квадратной. Определитель
матрицы
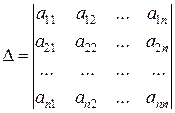
называется определителем системы.
Необходимым и достаточным условием того, что система (6) имеет единственное решение, является условие, что ее определитель д не равен нулю. Если D = 0, то решений может быть или бесконечное множество, если уравнения системы линейно зависимы, или не существовать ни одного, если уравнения противоречивы.
Эффективность способов решения СЛАУ во многом зависит от структуры и свойств матрицы А: размерности я, обусловленности, симметричности, заполненности (т.е. соотношения между числом нулевых и ненулевых элементов), специфики расположения ненулевых элементов в матрице и др.
Все существующие численные методы решения СЛАУ делятся на прямые и итерационные. Прямые методы дают точное решение задачи за конечное число операций, если все они выполняются без погрешностей округления. Эти методы сравнительно просты и наиболее универсальны, т.е. пригодны для решения широкого класса линейных систем. К прямым методам относятся методы исключения (Гаусса, Гаусса-Жордана и др.), декомпозиции и др. Итерационные методы позволяют находить приближенное решение СЛАУ путем построения последовательности приближений (итераций), начиная с некоторого начального приближения. К этому классу относятся методы простых итераций, Зейделя и множество других. Их достоинством является то, что они обладают свойством самоисправления ошибок в ходе вычислений. Недостатком является то, что они не всегда сходятся. Алгоритмы решения линейных систем с использованием итерационных методов обычно более сложные по сравнению с прямыми методами. Объем вычислений заранее определить трудно. Чаще всего итерационные методы применяются к большим системам уравнений с разреженными или слабозаполненными матрицами.
Методы исключения
Метод исключения Гаусса основан на приведение системы уравнений (6) к треугольному виду и является одним из наиболее часто используемых прямых методов решения СЛАУ. Процесс решения состоит из двух этапов.
1-й этап – прямой ход – система уравнений приводится к треугольному виду. Для этого на первом шаге из всех уравнений кроме первого, исключается неизвестное 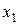 . На втором шаге из всех уравнений, кроме первого и второго исключается
. На втором шаге из всех уравнений, кроме первого и второго исключается 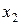 и т.д., пока не исключатся неизвестные
и т.д., пока не исключатся неизвестные 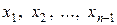 . В итоге приходим к новой системе уравнений
. В итоге приходим к новой системе уравнений
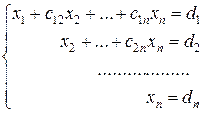 (7)
(7)
2-й этап – обратный ход. Из полученной системы уравнений (7) последовательно, начиная с последнего уравнения, определяются неизвестные 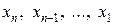 .
.
Если главные коэффициенты аи в системе (б) близки к нулю, то этот метод становится непригоден для нахождения решения. В этом случае применяют метод Гаусса с выбором главного элемента. Он заключается в том, что при прямом ходе производится выбор наибольшего по модулю (главного) элемента в рассматриваемом столбце и соответствующая перестановка строк. Это исключает деление на ноль при исключении неизвестных и повышает точность вычислений при наличии ошибок округления.
Усовершенствованной разновидностью метода Гаусса является метод Гаусса-Жордана. Если в методе Гаусса преобразования затрагивают только уравнения, стоящие под главной диагональю, то в методе Гаусса-Жордана преобразуются также и уравнения, стоящие над главной диагональю. В результате последовательного исключения неизвестных исходная матрица приводится к диагональному виду.
Достоинством этого метода является облегчение получения решения – не нужен обратный ход. Недостатком является увеличение числа операций по сравнению с классическим методом Гаусса.
Алгоритмы исключения неизвестных зарекомендовали себя на практике как эффективные и надежные методы. Тем не менее, и эти алгоритмы могут не привести к решению, если система уравнений плохо обусловлена. Говорят, что линейная система уравнений (6) является плохо обусловленной, если малые изменения элементов матрицы коэффициентов А или правых частей 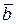 приводят к большим изменениям в решении
приводят к большим изменениям в решении 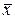 . В этом случае ни от какого численного метода нельзя ожидать, что он даст точное решение, а во многих случаях не следует даже и пытаться искать решение.
. В этом случае ни от какого численного метода нельзя ожидать, что он даст точное решение, а во многих случаях не следует даже и пытаться искать решение.
Пример 2.2. Решить методом Гаусса систему уравнений
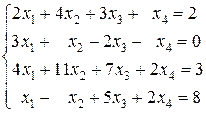 (8)
(8)
Решение
Прямой ход. 1-й шаг.
Разделим первое уравнение системы (8) на 2:
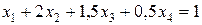 , (9)
, (9)
умножим уравнение (9) на (–3) и сложим со вторым уравнением системы (8):
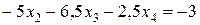 .
.
Умножим уравнение (9) на (–4) и сложим с третьим уравнением системы (8):
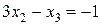 .
.
Вычтем уравнение (9) из четвертого уравнения исходной системы (8):
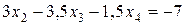 .
.
В результате всех преобразований получили новую систему уравнений
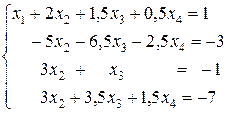 (10)
(10)
2-й шаг.
Разделим второе уравнение полученной системы (10) на (–5):
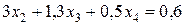 . (11)
. (11)
Умножим уравнение (11) на (–3) и сложим с третьим уравнением системы (10):
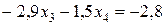 .
.
Умножим уравнение (11) на (–3) и сложим с четвертым уравнением системы (10):
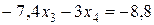 .
.
В итоге получили систему уравнений
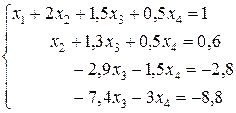 (12)
(12)
3-й шаг.
Делим третье уравнение полученной системы (12) на (–2,9):
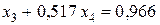 . (13)
. (13)
Умножим уравнение (13) на 7,4 и сложим с третьим уравнением системы (12):
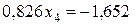 .
.
В итоге получили систему уравнений
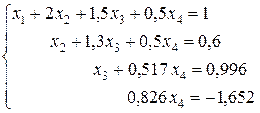
4-й шаг.
Делим четвертое уравнение полученной системы на 0,826:
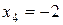 .
.
В результате всех преобразований получили треугольную систему уравнений
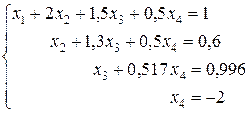
Обратный ход. Из этой системы уравнений последовательно находим
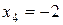 ;
;
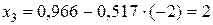 ;
;
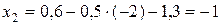 ;
;
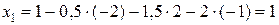 .
.
Проверка
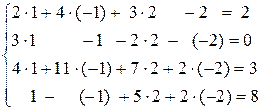
Дата: 2019-03-05, просмотров: 368.