Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Решить нелинейное уравнение 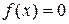 методом Ньютона с точностью 0,001 (табл. 1). Построить график функции .

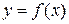Таблица 1

Вариант	Функция f(x)	Вариант	Функция f(x)
1.	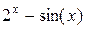,	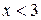6.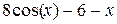
2.	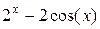,	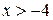7.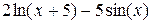
3.	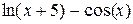,	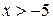8.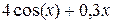
4.		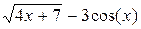9.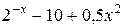
5.		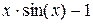10.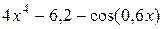

Задача 2. Решение систем линей­ных алгебраических урав­нений

Решить систему линейных алгебраических уравнений методом Гаусса (табл. 2).

Таблица 2

Вари­ант	Система уравнений	Вари­ант	Система уравнений
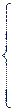
1.	2x1 + Зx2 – x 3  + x 4 = –3 Зx1 –  x2  + 2x3 + 4x4 = 8 x 1 + x 2  + Зx3 – 2x4 = 6 –x1 + 2 x 2  + Зx3 + 5x4 = 3	2.	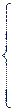x1 + 2 x 2 – Зx3 + x4 = –9 3x1 – 4x2 +2x3 – 2x4 = 15 2 x 1 + 2 x 2 + Зx3 + Зx4 = 0 5 x 1 – x 2 – 2 x3 – 5x4 = 12
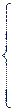
3.	x1 + 2x2 – З x3 + 2x4 = 3 2x1 + З x2 +x3 –x4 = 6 3x1 – x2 – 2x3 – x4 = 9 4x1 + З x2 – 5x3 – 2x4 = 1	4.	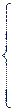2 x 1 + 3 x 2 – x 3 + x 4 = –4 3 x 1 – x 2 + 2x3 + 4x4 = 9 x1 + x2 + Зx3 – 2x4 = 3 3x1 + 2 x2 + x3 + 5 x4 = 5
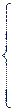
5.	x1 + x2 – x3 + x4 = 3 2x1 – x2 – x3 – x4 = –1 Зx1 + 2x2 – 6x3 + 2x4 = 0 x 1 – 2x2 + 4x4 = 2	6.	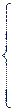x1 + 2x2 – x3 + x4 = 1 Зx1 – x2 + 2 x 3 + x4 = –1 2 x 1 – 2 x 2 + 3 x 3 = 5 2x1 + 3 x 2 – 2 x 3 + x4 = –3
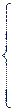
7.	x1 – 2x3 + Зx4 = –4 x2 – Зx3 + 4x4 = –5 3 x1 + 2 x2 –5x4 = 12 4x 1 + 3x2 – 5x3 = 5	8.	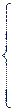x 1 – 3 x 2 + 5 x 3 – 7x4 = 12 3 x 1 – 5 x 2 + 7 x 3 – x 4 = 0 5 x 1 – 7 x 2 + x 3 – 3x4 = 4 7 x1 – x2 + 3 x3 – 5 x4 = 16
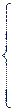
9.	2x1 + Зx2 – Зx3 + 4x4 = 7 2x1 +  x 2 – x3 + 2x4 = 5 6 x1 + 2x2 + x3 = 4 2x1 + Зx2 – 5x4 = –11	10.	x1 + x2 – x3 + x4 = –4 2x1 – x2 + Зx3 – 2x4 = 1 x1 – x3 + 2x4 = 6 3x1 – x2 + x3 – x4 = 0

 

 

Задача 3. Вычисление определенных интегралов

Вычислить определенный интеграл 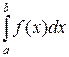 методом Симпсона.

Отрезок интегрирования [a,b] разбить на десять частей (табл. 3).

 

                                                                             Таблица 3

Вариант	Функция f(x)	a	b	Вариант	Функция f(x)	a	b
1.		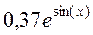0	1	6.		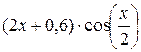1	2
2.		1	2	7.		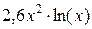1,2	2,2
3.		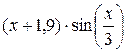1	2	8.		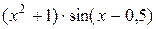0,5	1,5
4.		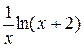2	3	9.		2	3
5.		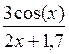0	1	10.		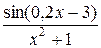3	4

 

Задача 4. Решение дифференциальных уравнений

Решить задачу Коши для обыкновенного дифференциального уравнения 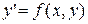 на отрезке [а, b] с начальным условием  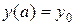и шагом интегрирования h методом Рунге-Кутта (табл. 4). Построить график полученной кривой.

                                                              Таблица 4

Вариант	Функция f ( x,y)	а	b	y0	h
1.		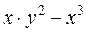1	2	0,7	0,1
2.		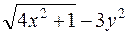2,6	4,6	1,8	0,2
3.		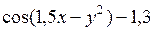-1	1	0,2	0,2
4.		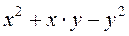2	3	1,2	0,1
5.		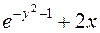0	0,5	0,3	0,05
6.		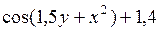1	2	0,9	0,1
7.		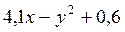0,6	2,6	3,4	0,2
8.		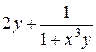1,5	2	2,1	0,05
9.		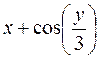2,1	3,1	2,5	0,1
10.		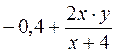3	5	1,7	0,2

 

 

Задача 5. Задачи регрессии

Методом наименьших квадратов построить линейную функцию для табличных данных (табл. 5). Нарисовать график полученной функции и показать исходные данные.

                                                                            Таблица 5

Значения x	-4	-3	-2	-1	0	1	2	3	4	5
Вариант	Значения y
1.	-3,32	-3,64	-3,57	3,54	2,75	4,02	5,24	5,79	7,48	13,49
2.	-3,51	-1,68	1,1	-2,2	3,81	4,79	2,51	5,7	8,84	11,72
3.	-4,66	-3,5	0,7	-2,39	-0,06	2,47	5,74	4,83	6,18	8,51
4.	-7,49	-4,4	-0,28	-0,82	-1,15	4,38	7,26	7,31	7,92	9,6
5.	-3,25	-2,07	-2,23	-1,24	4,9	2,92	8,25	5,15	6,53	11,23
6.	-5,35	-1,5	-0,86	0,27	0,49	3,63	7,78	6,27	8,33	13,07
7.	-2,36	-5,62	-3,53	-1,64	-0,66	5,24	7,89	7,87	7,83	10,96
8.	-5,44	-1,57	-0,23	-0,46	-0,29	5,86	8,07	5,01	6,28	7,55
9.	-7,13	-1,88	-1,06	-0,17	2?65	1,2	2,71	6,19	6,59	8,38
10.	-4,94	-2,25	0,67	-1,57	2,49	2,7	6,26	5,88	9,44	10,1

Численные методы решения задач

Решение нелинейных уравнений

Математические модели реальных объектов, как правило, описываются нелинейными уравнениями. Нахождение корней нелинейных уравнений - одна из древнейших математических проблем, которая не потеряла своей остроты и в наши дни: она часто встречается в самых разнообразных областях науки и техники.

Постановка задачи

Требуется найти такие значения аргумента x, для которых справедливо уравнение

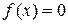                                                               (1)
где функция 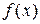 дифференцируема. При этом уравнение (1) может быть алгебраическим или трансцендентным*.

Корень x уравнения (1) геометрически представляет собой абсциссу точки пересечения (рис. 1а), точки касания (рис. 1б) или другой общей точки (рис. 1в) графика функции 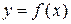 и оси х.

 

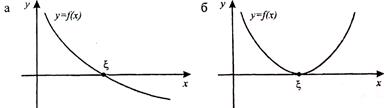
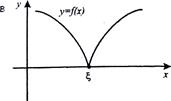
Рис. 1

 

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни уравнения (1) в виде некоторого конечного соотношения (формулы). Примером такого решения является нахождение корней квадратного уравнения, известного из школьного курса алгебры.

В дальнейшем будут рассматриваться только уравнения, которые, как правило, не имеют аналитических формул для вычисления корней уравнения. Для них приходится пользоваться итерационными методами нахождения решения, которые состоят из двух этапов:

1. Отыскание приближенного значения корня (отделение корня), т.е. нахождение такого конечного промежутка, внутри которого имеется единственное решение данного уравнения (1). Отделение корней можно осуществить аналитическим (находя критические точки функции) и графическим (путем построения графика функции) способами.

Для отделения корней применяют следующий критерий: если на отрезке [a; b] функция 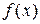 непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то этот отрезок содержит один и только один корень уравнения (1). Достаточным признаком монотонности функции  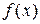на некотором отрезке является сохранение знака ее производной на этом отрезке (если 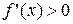, то функция возрастает; если 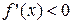, функция убывает).

2. Уточнение приближенного значения до некоторой заданной степени точности.

В практических задачах решением называют любое значение аргумента x отличающееся по модулю от точного значения корня x не более чем на малую величину e.

В общем случае итерационный процесс состоит в последовательном уточнении начального приближения х₀. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня х₁, х₂, ..., х_к, ... Если эти значения с ростом k стремятся к истинному значению корня

                        ,
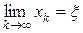то говорят, что итерационный процесс сходится.

Метод Ньютона

В основе метода Ньютона (метода касательных) лежит разложение функции  f(x) в ряд Тейлора:

    

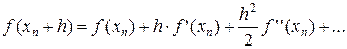
Члены, содержащие h во второй и более высоких степенях, отбрасываются, используется соотношение 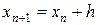 и предполагается, что  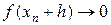при 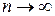. Отсюда получается итерационная формула

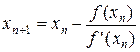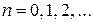              ,              (2)

 

Графическое представление метода показано на рис. 2. В точке (х₀, f(х₀)) проводят касательную к графику функции f(x) и точку пересечения ее с осью х принимают за новое приближение x₁. Для него строят новую касательную, находят точку х₂ и т.д. до тех пор, пока значение 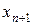 не станет достаточно близко к корню x.

Счет прекращается, когда выполняется условие

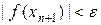                        .                               (3)

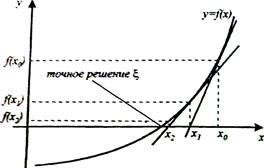
Рис. 2

 

Метод Ньютона обладает квадратичной скоростью сходимости для .достаточно гладких функций f(x). Быстрота его сходимости в большой степени зависит от выбора начального приближения х₀. Метод обеспечивает быструю сходимость, если выполняется неравенство

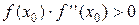              ,                                      (4)
поэтому чаще всего в качестве начального приближения выбирают тот конец интервала [а; b], на котором знаки f и f ’’ совпадают (условие Фурье).

Достоинством этого метода является его быстрая сходимость, а недостатком то, что помимо 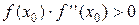 надо вычислять и 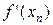, поэтому метод применим, если вычисление производной f ' не сложнее, чем вычисление функции  f.

 

Пример 2.1. Найти корень уравнения

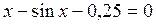                                   (5)

с точностью e = 0,001 методом Ньютона.

 

 

Решение

1. Обозначим левую часть уравнения как функцию .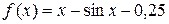

2. Вычислим первую и вторую производные:

     ,
          .

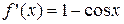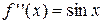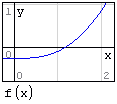3. Построим график функции и определим по нему отрезок, на котором функция пересекает ось x. В данном примере на графике видим, что f(x) обращается в нуль на отрезке от 0 до 2. Отрезок следует выбрать так, чтобы на нем было только одно пересечение f(x) с осью x.

 

4. Проверим выполнение условия Фурье ( 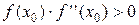) на границах заданного интервала [0;2].

Подставляем левую границу интервала :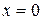

     ,
          .

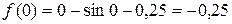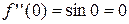Произведение 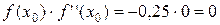, т.е. условие Фурье не выполняется.

Подставляем правую границу интервала :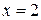

, 

.

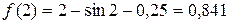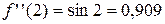Произведение 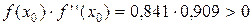, т.е. условие Фурье выполняется. Поэтому за начальное приближение  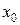принимаем правую границу интервала: .

 

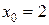5. Первая итерация. Найдем уточненное значение :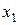

      .

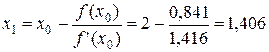Найдем модуль функции для значения :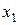

     .

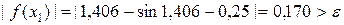Поскольку условие 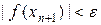 не выполняется, то делаем следующую итерацию.

6. Вторая итерация. Найдем уточненное значение :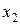

     ,

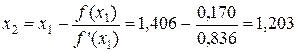Найдем модуль функции для значения :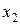

     .

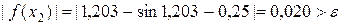Поскольку условие 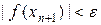 не выполняется, то делаем следующую итерацию.

7. Третья итерация. Найдем уточненное значение :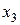

     ,

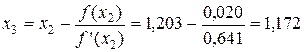Найдем модуль функции для значения :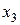

     .

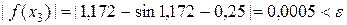Условие 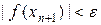 выполняется, решение найдено с заданной точностью.

8. Ответ: На отрезке 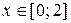 корень уравнения  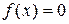равен  х = 1,172 с точностью e = 0,001.