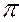Сущность способа перемены плоскостей проекций заключается в том, что положение точек, плоских фигур, поверхностей в пространстве остаётся неизменным, а система плоскостей проекций ₁, ₂ дополняется плоскостями, образующими с 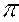₁ или 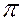₂ (или между собой) системы двух взаимно перпендикулярных плоскостей. Например, плоскость 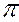₄ перпендикулярна плоскости 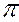₁ ( на рис.53,54).

Нахождение проекции точки А в этом случае представлено на рис.54.

Рис. 53 Способ перемены плоскостей проекций

Сохраняющаяся А' и новая А^IV проекции точки связаны линией проекционной связи, перпендикулярной к новой оси проекций ₁/ ₄ . На этой линии связи от новой оси откладывается отрезок равный расстоянию от заменяемой проекции А" до заменяемой оси Х.

Каждая новая система плоскостей выбирается так, чтобы получилось положение наиболее удобное для требуемого построения.

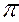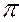Часто бывает достаточно введение только одной дополнительной плоскости ₄, перпендикулярной плоскости ₁  или ₂.

Иногда вводят несколько дополнительных плоскостей проекций, например: плоскость ₄, перпендикулярную плоскости 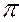₂, затем плоскость 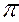₅, перпендикулярную плоскости ₄. При этом плоскость ₅ оказывается плоскостью общего положения в основной системе плоскостей ₁, ₂.

Рис.54 Проекция точки на плоскость ₄

Метод перемены плоскостей проекций позволяет решить целый ряд позиционных задач:

1) Определить натуральную величину отрезка.

Для этого вводят новую плоскость проекции ₄ , перпендикулярную плоскости 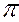₁ (рис.55), а новую ось ₁/ ₄ располагают параллельно горизонтальной проекции отрезка А^IB^I. Таким образом А^IVB^IV истинная длина отрезка АВ, угол α – угол наклона отрезка к плоскости ₁.

Рис.55 Определение натуральной величины отрезка

2) Преобразовать плоскости общего положения в плоскость проецирующую (рис.56).

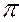Новую ось ₁/ ₄ проводят перпендикулярно горизонтальному (как в данном примере, либо – фронтальному) следу заданной плоскости α. Если плоскость задана треугольником, то для преобразования её в проецирующую новую ось ₁/ 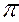₄ проводят перпендикулярно горизонтальной проекции горизонтали (рис.57) либо перпендикулярно фронтальной проекции фронтали.

Рис.56 Преобразование плоскости в проецирующую

3) Найти натуральную величину треугольника АВС (рис.57).

Для этого введём ещё одну дополнительную плоскость ₄/ 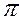₅ и, расположив её параллельно проекции треугольника на плоскости ₄  (А^IV, B^IV, С^IV ), найдём проекцию треугольника на плоскость ₅ (А^VB^V С^V ). Эта проекция и будет представлять собой натуральную величину треугольника АВС.

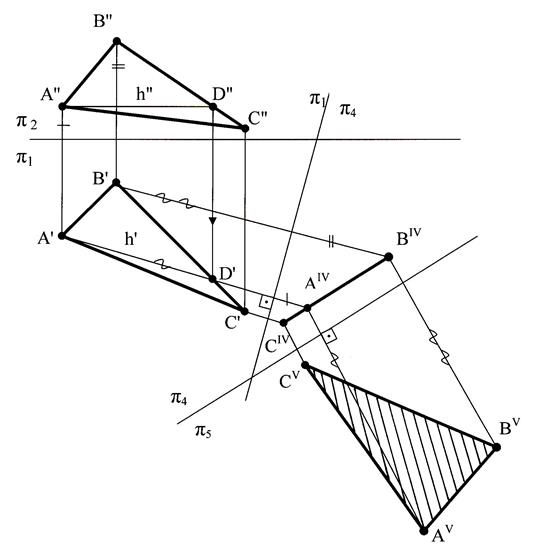
Рис.57 Определение натуральной величины треугольника

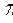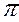4) Определить расстояние между двумя параллельными прямыми АВ и СД (рис.58). Потребуется дважды проводить перемену плоскостей проекций. Вначале ось ₁/ ₄ располагают параллельно одной из проекций прямых, например горизонтальной. Вторую перемену плоскостей проекций проводят таким образом, чтобы прямые спроецировались в точки, т.е. ось 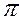₄/ 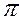₅ располагают перпендикулярно проекциям А^IVB^IV  и С^IVD^IV. Тогда расстояние между точками А^VB^V и С^VD^V определит расстояние между прямыми АВ и СD в пространстве.

Рис. 58 Определение расстояния между параллельными прямыми

5) Определить расстояние от точки до плоскости. Для этого заданную плоскость общего положения α нужно преобразовать  в проецирующую. А также найти проекцию точки К в новой системе плоскостей проекций 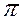₁/ 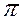₄  (К^IV) (рис.59).

Рис.59 Определение расстояния от точки до плоскости

Поскольку кратчайшим расстоянием от точки до плоскости является перпендикуляр, то опустив из проекции точки К^IV перпендикуляр на след 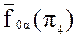, получим натуральную величину расстояния от точки К до плоскости α.

    Рассмотренные в данной работе примеры демонстрируют лишь часть геометрических задач, которые позволяет решать способ перемены плоскостей проекций.

Библиографический список

1.Гордон В.О., Семенцов-Огиевский Н.А. Курс начертательной геометрии.  М.: Высшая школа, 2007.272с.

2.Фролов С.А., Начертательная геометрия. М.: Машиностроение, 2002.240с.

С о д е р ж а н и е

1. Предмет начертательной геометрии. 3

1.1 Проекции центральные. 3

1.2 Проекции параллельные. 4

1.3 Метод Монжа. 6

1.4 Точка в системе двух плоскостей проекций. 6

1.5 Точка в системе трех плоскостей проекций. 8

2. Проекции отрезка прямой линии. Прямые общего и частного положения 10

2.1 Прямые частного положения. 11

2.2 Взаимное положение двух прямых. 15

3. Следы прямой. 18

4. Определение натуральной величины отрезка методом прямоугольного треугольника. 21

5. Проекция плоскости. Следы плоскости. 22

5.1 Следы плоскости. 23

5.2 Плоскости частного положения. 25

5.3 Прямая и точка в плоскости. Главные линии плоскости. 30

5.4 Линии уровня. 32

6. Взаимное положение прямой и плоскости. 33

6.1 Пересечение прямой линии с плоскостью, перпендикулярной к одной или двум плоскостям проекций. 35

6.2 Пересечение прямой линии с плоскостью общего положения. 36

6.3 Построение прямой линии и плоскости, параллельных между собой 39

6.4 Построение взаимно перпендикулярной прямой и плоскости. 40

7. Взаимное положение плоскостей. 42

7.1 Параллельные плоскости. 43

7.2 Пересекающиеся плоскости. 45

7.3 Построение взаимно перпендикулярных плоскостей. 50

8. Способ перемены плоскостей проекций. 52

Учебное издание

Карклина Татьяна Осиповна

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Конспект лекций

Учебно-методическое пособие