НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Конспект лекций
Санкт-Петербург
2011
УДК
ББК
Рецензент:
кандидат технических наук, доцент Санкт-Петербургского государственного университета водных коммуникаций
В.Я.Готлиб
Карклина Т.О.
Начертательная геометрия. Конспект лекций:, учебно-методическое пособие - СПб.: СПГУВК, 2011. - 61 с.
Излагаются разделы начертательной геометрии и инженерной графики, входящие в дисциплину “Начертательная геометрия. Инженерная графика”.
Учебно-методическое пособие предназначено для студентов очной и заочной форм обучения следующих специальностей:
140604.65 “Электропривод и автоматика промышленных установок и технологических комплексов”
180101.65 “Кораблестроение”
180103.65 “Судовые энергетические установки”
180402.65 “Судовождение”
180403.65 “Эксплуатация судовых энергетических установок”
180404.65 “Эксплуатация судового электрооборудования и средств автоматики”
190602.65 “Эксплуатация перегрузочного оборудования портов и транспортных терминалов”
190701.65 “Организация перевозок и управление на транспорте”
270104.65 “Гидротехническое строительство”
280302.65 “Комплексное использование и охрана водных ресурсов”
УДК
ББК
© Карклина Т.О., 2011
©Санкт-Петербургский государственный университет водных коммуникаций, 2011
Предмет начертательной геометрии
Начертательная геометрия, как и другие разделы математики, входит в число фундаментальных дисциплин, составляющих основу инженерного образования.
Предметом начертательной геометрии является обоснование методов построения изображений пространственных форм на плоскости и способов решения геометрических задач по заданным изображениям этих форм.
Начертательная геометрия вызывает усиленную работу пространственного воображения, а также передает ряд своих выводов в практику выполнения технических чертежей, обеспечивая их выразительность и точность.
Правила построения изображений в начертательной геометрии основаны на методе проекций.
Рассмотрение метода проекций начинают с построения проекций точки, так как любая пространственная форма рассматривается как ряд точек.
Проекции центральные
При центральном проецировании задаётся плоскость проекций (обозначается строчными буквами греческого алфавита 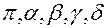 и другими ) и центр проекций – точка (обозначается прописными буквами латинского алфавита – A, B, … S и т.д.), не лежащая в данной плоскости (рис.1.).
и другими ) и центр проекций – точка (обозначается прописными буквами латинского алфавита – A, B, … S и т.д.), не лежащая в данной плоскости (рис.1.).
Взяв некоторую произвольную точку в пространстве (например (∙) А), проведем через неё и центр проекций S прямую до пересечения с
плоскостью проекций  0. Получим А0 – проекцию точки А на плоскость
0. Получим А0 – проекцию точки А на плоскость  0. Так же поступим с произвольными точками в пространстве В и С.
0. Так же поступим с произвольными точками в пространстве В и С.
В0, С0 - центральные проекции (∙) В и (∙) С на плоскость  0.
0.
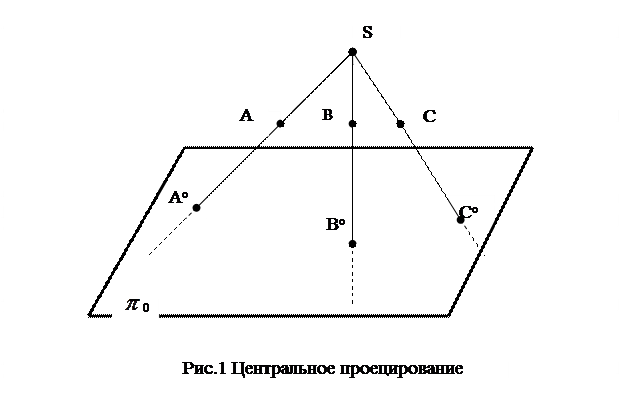
Но в данном случае, имея проекцию точки, нельзя однозначно определить положение самой точки в пространстве, так любая точка, лежащая на проецирующей прямой SA, проецируется в А0. Для единственного решения необходимы дополнительные условия.
Проекции параллельные
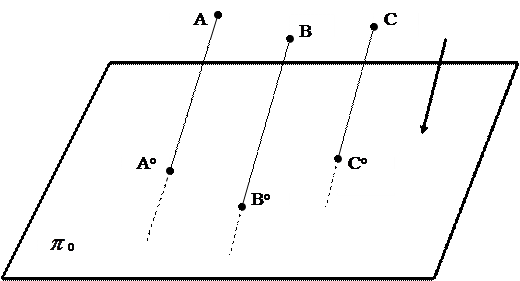
Если принять, что центр проекций бесконечно удалён от плоскости проекций, то проецирующие прямые будут параллельны между собой. Для их проведения должно быть указано некоторое направление (рис.2).
 | |||
| |||
Следовательно, параллельной проекцией точки называется точка пересечения проецирующей прямой, проведенной параллельно заданному направлению, с плоскостью проекций.
Существуют правила, распространяющиеся как на центральное проецирование, так и на параллельное:
1. Для прямой линии проецирующей поверхностью в общем случае служит плоскость, потому прямая проецируется в виде прямой;
2. Каждая точка и линия в пространстве имеют единственную свою проекции;
3. Каждая точка на плоскости может быть проекцией множества точек;
4. Каждая линия на плоскости может быть проекцией множества линий;
5. Для построения проекций прямой достаточно спроецировать две её точки;
6. Если прямая параллельна направлению проецирования, то её проекция является точкой;
7. Отрезок прямой, параллельный плоскости проекций, проецируется в натуральную величину.
Метод Монжа
Метод параллельного ортогонального проецирования был развит в трудах французского учёного Монжа.
Гаспар Монж (1746-1818) – крупный геометр и государственный деятель периода правления Наполеона. Его труд по начертательной геометрии долго не публиковался, так как имел большое практическое значение для выполнения чертежей военных объектов, и увидел свет только в конце 18 века. Изложенный Монжем метод параллельного ортогонального (т.е., прямоугольного) проецирования до сих пор остается основным методом составления технических чертежей, обеспечивая выразительность, точность и удобоизмеримость предметов на плоскости.
Прямые частного положения
Наряду с прямыми общего положения существуют прямые, расположенные особым образом относительно плоскостей проекций. Их называют прямыми частного положения и подразделяют на следующие виды:
Следы прямой
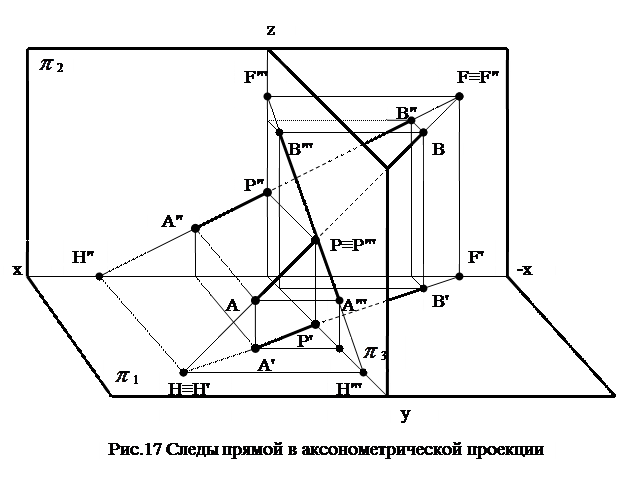
Горизонтальным (фронтальным, профильным) следом прямой называется точка пересечения прямой с горизонтальной (фронтальной, профильной) плоскостью проекций (рис.17).

Прямая не имеет следа на плоскости проекций в том случае, когда она параллельна этой плоскости.
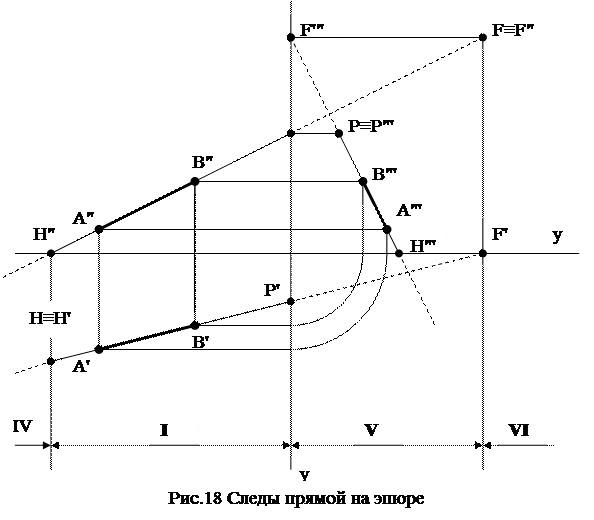
На рис. 17 изображен отрезок прямой общего положения АВ и три его проекции А'В', А"В", А"'В"'. Продолжив отрезок до пересечения с горизонтальной плоскостью проекций 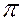 1, получим точку пересечения Н, которая является горизонтальным следом прямой АВ. Как любая точка в системе ортогонального параллельного проецирования, она будет иметь три проекции. Найдем их, помня о том, что точка Н помимо всего прочего лежит на прямой АВ, а, следовательно, каждая её проекция должна находиться на одноимённой проекции прямой. Таким образом получим Н"ЄА"В" и ЄОХ, Н"'ЄА"'В"' и ЄОY. Горизонтальная проекция Н' совпадает с самим следом Н, так как по определению НЄ плоскости
1, получим точку пересечения Н, которая является горизонтальным следом прямой АВ. Как любая точка в системе ортогонального параллельного проецирования, она будет иметь три проекции. Найдем их, помня о том, что точка Н помимо всего прочего лежит на прямой АВ, а, следовательно, каждая её проекция должна находиться на одноимённой проекции прямой. Таким образом получим Н"ЄА"В" и ЄОХ, Н"'ЄА"'В"' и ЄОY. Горизонтальная проекция Н' совпадает с самим следом Н, так как по определению НЄ плоскости 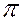 1.
1.

Аналогичным образом рассуждаем при построении фронтального и профильного следов и их проекций.
|
Алгоритм построения следов прямой (рис.18):
1. Находим точку пересечения фронтальной проекции прямой (или её продолжения) с осью Х. В этой точке находится фронтальная проекция горизонтального следа Н".
2. Из точки Н" восстанавливаем перпендикуляр к оси Х до пересечения с горизонтальной проекцией прямой. В точке пересечения получим горизонтальный след прямой Н и его горизонтальную проекцию Н'.
3. Находим точку пересечения горизонтальной проекции прямой с осью Х, получив в этой точке горизонтальную проекцию фронтального следа F'.
4. Из точки F' восстанавливаем перпендикуляр к оси Х до пересечения с фронтальной проекцией прямой. В точке пересечения получаем фронтальный след прямой F и его фронтальную проекцию F".
5. Находим точку пересечения фронтальной проекции прямой с осью Z. В этой точке будет находиться фронтальная проекция профильного следа Р".
6. Из точки Р" восстанавливаем перпендикуляр к оси Z до пересечения с профильной проекцией прямой. В точке пересечения получим профильный след прямой Р и его профильную проекцию Р"'.
7. Находим недостающие проекции следов Н"', F"', Р', помня о том, что это точки, лежащие на прямой АВ, а следовательно каждая их проекция находится на соответствующей проекции прямой.
8. Определяем октанты, через которые проходит прямая и устанавливаем её видимость (прямая считается видимой только в I октанте).
Следы плоскости
Более наглядно плоскость может быть задана следами.
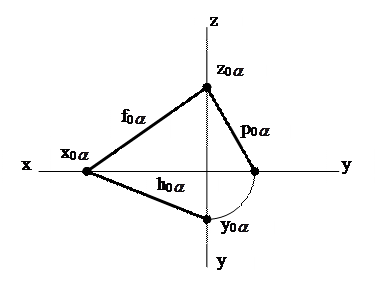
Следы плоскости – это линии, по которым плоскость пересекается с плоскостями проекций. На чертеже они обозначаются следующим образом: h0 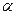 - горизонтальный след плоскости; f0
- горизонтальный след плоскости; f0 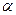 - фронтальный и p0
- фронтальный и p0 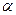 - профильный (рис.22).
- профильный (рис.22).
а)
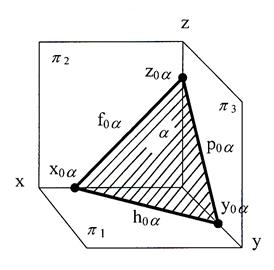
| б)
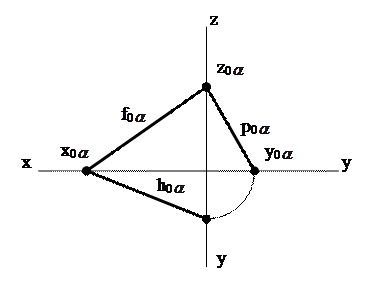 
|
| Рис. 22 Следы плоскости общего положения: а) в аксонометрической проекции; б) на эпюре
| |
Плоскость, заданную любым из перечисленных выше способов, можно преобразовать в плоскость, заданную следами.
Предположим, плоскость β задана пересекающимися прямыми (рис.23). Для построения прямой, по которой плоскость β пересечет горизонтальную плоскость проекций 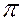 1 (т.е. горизонтального следа плоскости h0β), достаточно найти две точки, которые одновременно принадлежали бы плоскости β и плоскости
1 (т.е. горизонтального следа плоскости h0β), достаточно найти две точки, которые одновременно принадлежали бы плоскости β и плоскости 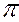 1. Такими точками будут горизонтальные следы прямых m и n, соответственно Н m , Нn.
1. Такими точками будут горизонтальные следы прямых m и n, соответственно Н m , Нn.
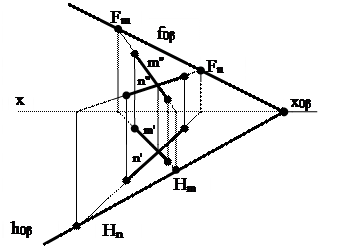
Рис. 23 Преобразование плоскости, заданной пересекающимися прямыми, в плоскость, заданную следами
Соединив точки Нm и Нn получим горизонтальный след плоскости h0β. Для построения фронтального следа плоскости найдём фронтальный след прямой m - Fm и фронтальный след прямой n - Fn. Соединив полученные точки (Fm и Fn), получим фронтальный след плоскости f0β.
х0β – точка пересечения следов (f0 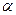 и f0β ) на оси Х, называемая точкой схода следов.
и f0β ) на оси Х, называемая точкой схода следов.
Угол между следами на чертеже не равен углу между следами в пространстве ( это видно из рассмотрения трёхгранного угла на рис.22).
Плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций называется плоскостью общего положения (рис.22, 23).
Линии уровня
К числу прямых, занимающих особое положение в плоскости, относятся горизонтали , фронтали и линии наибольшего наклона к плоскостям проекций, их называют линиями уровня. Линию наибольшего наклона к плоскости 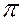 1 называют линией наибольшего ската плоскости С, её проекции С' и С" (рис. 34).
1 называют линией наибольшего ската плоскости С, её проекции С' и С" (рис. 34).
Горизонтали плоскости h (проекции h' и h") – линии, лежащие в ней и параллельные горизонтальной плоскости проекций 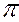 1.
1.
Фронтали плоскости f (проекции f' и f") – линии, лежащие в ней и параллельные фронтальной плоскости проекций 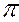 2.
2.
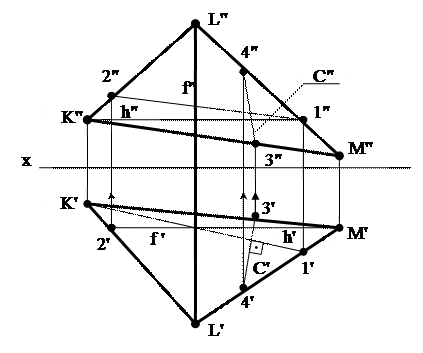
Рис. 34 Линия уровня в плоскости
Линиями наибольшего наклона плоскости к плоскостям проекций 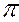 1,
1, 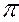 2,
2, 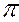 3 называют прямые, лежащие в ней и перпендикулярные к горизонталям, фронталям или профильным прямым плоскости соответственно.
3 называют прямые, лежащие в ней и перпендикулярные к горизонталям, фронталям или профильным прямым плоскости соответственно.
Линия наибольшего ската плоскости – линия, лежащая в плоскости, определяющая угол наибольшего наклона заданной плоскости к горизонтальной плоскости проекций и перпендикулярная к горизонтали. Согласно правилам проецирования прямого угла (теорема о проецировании прямого угла), горизонтальная проекция линии ската перпендикулярна горизонтальной проекции горизонтали.
Параллельные плоскости
Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны между собой.


Рис. 43 Плоскости, параллельные между собой
Пример:
Дана плоскость, треугольник АВС. Через точку М провести плоскость β, параллельную заданной. Через заданную точку М проведем две пересекающиеся прямые (рис.43), которые определяют собой искомую плоскость β, параллельные сторонам треугольника АВС: MN║АВ, МК║ВС.
Если два пересекающихся между собой следа одной плоскости параллельны двум пересекающимся следам другой плоскости, то эти плоскости параллельны (рис.44).
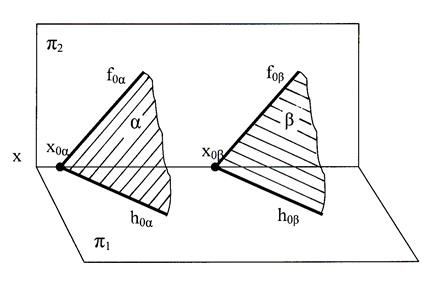
Рис. 44 Параллельные плоскости общего положения,
заданные следами
Если параллельны не пересекающиеся следы, надо построить профильные следы (рис.45) и по их положению определить взаимное положение плоскостей.
а) б)
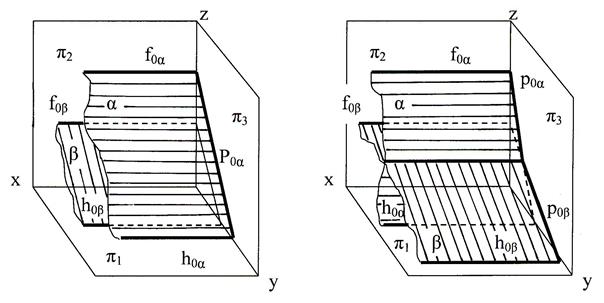
Рис. 45 Профильно-проецирующие плоскости:
а) параллельные; б) пересекающиеся
Пересекающиеся плоскости
Если хотя бы одна пара следов пересекается, то плоскости пересекаются.
Линия пересечения двух плоскостей вполне определяется двумя точками, каждая из которых принадлежит обеим плоскостям (рис.46). MN – линия пересечения плоскостей общего положения α и β, где точки М и N являются следами линии пересечения.


Если одна из плоскостей проецирующая (в данном случае плоскость α – горизонтально-проецирующая), то линия пересечения очевидна – это линия 1-2 (рис.47).
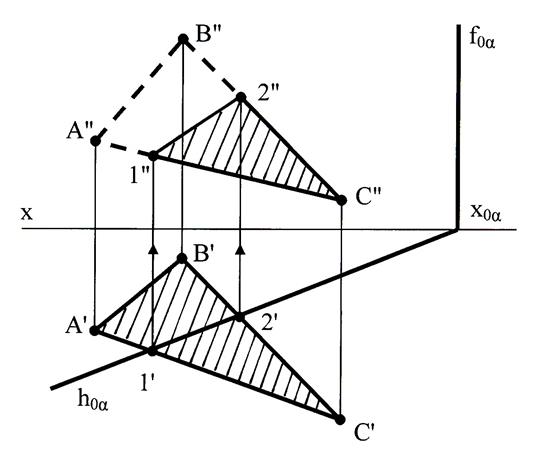
Рис.47 Пересечение треугольника
горизонтально-проецирующей плоскостью
Если одна из плоскостей плоскость β параллельна плоскости 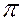 1 (рис.48), т.е. горизонтальная, а вторая плоскость общего положения α, то линией их пересечения будет горизонталь МN.
1 (рис.48), т.е. горизонтальная, а вторая плоскость общего положения α, то линией их пересечения будет горизонталь МN.
а) б)
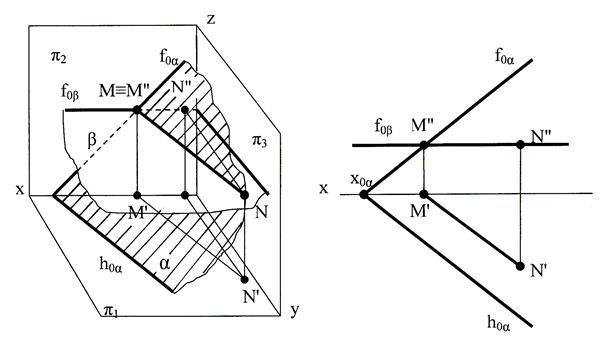
Рис. 48 Пересечение плоскости общего положения с горизонтальной плоскостью: а) в аксонометрической проекции; б) на эпюре
Теперь рассмотрим случай построения линии пересечения двух плоскостей, когда одна из плоскостей α задана следами, а другая β – треугольником АВС. Построение показано на рис.49. Для определения положения линии пересечения К1 и К2 заданных плоскостей возьмём две вспомогательные горизонтальные плоскости (γ1 и γ2), пересекающие каждую из плоскостей α и β. При пересечении заданных плоскостей плоскостью γ1 получаем прямые с проекциями А'1', А"1", и h1' , h1".
Эти прямые, расположенные в плоскости γ1, в своём пересечении определяют первую точку К1 линии пересечения плоскостей α и β.
Введя далее плоскость γ2 , получаем в её пересечении с плоскостями α и β прямые с проекциями 2'3', 2"3" и h2', h2". Эти прямые, расположенные в плоскости γ2, в своём пересечении определяют вторую точку К2, общую для α и β. Таким образом определена линия пересечения (К1'К2' – её горизонтальная проекция, К1"К2" – её фронтальная проекция) заданных плоскостей α и β.


Рис. 49 Построение линии пересечения плоскостей
Построение линии пересечения двух плоскостей по точкам пересечения прямых линий с плоскостью приведено на рис. 50. В качестве плоскостей фигурируют треугольники АВС и DEF.
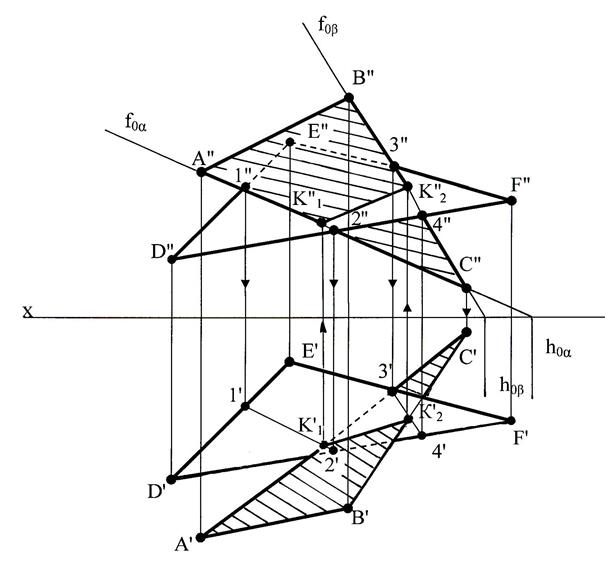
Рис. 50 Пересечение треугольников
Прямая К1К2 построена по точкам пересечения сторон АС и ВС треугольника АВС с плоскостью треугольника DEF. Вспомогательная фронтально-проецирующая плоскость α, проведённая через АС, пересекает треугольник DEF по прямой с проекциями 1"2" и 1'2'. В пересечении проекций 1'2' и А'С' получена горизонтальная проекция К1'. Затем построена К1". Аналогичным образом, используя вспомогательную фронтально-проецирующую плоскость β, найдены проекции точки К2', К2". Видимость треугольников определена методом конкурирующих точек.
С о д е р ж а н и е
1. Предмет начертательной геометрии. 3
1.1 Проекции центральные. 3
1.2 Проекции параллельные. 4
1.3 Метод Монжа. 6
1.4 Точка в системе двух плоскостей проекций. 6
1.5 Точка в системе трех плоскостей проекций. 8
2. Проекции отрезка прямой линии. Прямые общего и частного положения 10
2.1 Прямые частного положения. 11
2.2 Взаимное положение двух прямых. 15
3. Следы прямой. 18
4. Определение натуральной величины отрезка методом прямоугольного треугольника. 21
5. Проекция плоскости. Следы плоскости. 22
5.1 Следы плоскости. 23
5.2 Плоскости частного положения. 25
5.3 Прямая и точка в плоскости. Главные линии плоскости. 30
5.4 Линии уровня. 32
6. Взаимное положение прямой и плоскости. 33
6.1 Пересечение прямой линии с плоскостью, перпендикулярной к одной или двум плоскостям проекций. 35
6.2 Пересечение прямой линии с плоскостью общего положения. 36
6.3 Построение прямой линии и плоскости, параллельных между собой 39
6.4 Построение взаимно перпендикулярной прямой и плоскости. 40
7. Взаимное положение плоскостей. 42
7.1 Параллельные плоскости. 43
7.2 Пересекающиеся плоскости. 45
7.3 Построение взаимно перпендикулярных плоскостей. 50
8. Способ перемены плоскостей проекций. 52
Учебное издание
Карклина Татьяна Осиповна
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Конспект лекций
Учебно-методическое пособие
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Конспект лекций
Санкт-Петербург
2011
УДК
ББК
Рецензент:
кандидат технических наук, доцент Санкт-Петербургского государственного университета водных коммуникаций
В.Я.Готлиб
Карклина Т.О.
Начертательная геометрия. Конспект лекций:, учебно-методическое пособие - СПб.: СПГУВК, 2011. - 61 с.
Излагаются разделы начертательной геометрии и инженерной графики, входящие в дисциплину “Начертательная геометрия. Инженерная графика”.
Учебно-методическое пособие предназначено для студентов очной и заочной форм обучения следующих специальностей:
140604.65 “Электропривод и автоматика промышленных установок и технологических комплексов”
180101.65 “Кораблестроение”
180103.65 “Судовые энергетические установки”
180402.65 “Судовождение”
180403.65 “Эксплуатация судовых энергетических установок”
180404.65 “Эксплуатация судового электрооборудования и средств автоматики”
190602.65 “Эксплуатация перегрузочного оборудования портов и транспортных терминалов”
190701.65 “Организация перевозок и управление на транспорте”
270104.65 “Гидротехническое строительство”
280302.65 “Комплексное использование и охрана водных ресурсов”
УДК
ББК
© Карклина Т.О., 2011
©Санкт-Петербургский государственный университет водных коммуникаций, 2011
Предмет начертательной геометрии
Начертательная геометрия, как и другие разделы математики, входит в число фундаментальных дисциплин, составляющих основу инженерного образования.
Предметом начертательной геометрии является обоснование методов построения изображений пространственных форм на плоскости и способов решения геометрических задач по заданным изображениям этих форм.
Начертательная геометрия вызывает усиленную работу пространственного воображения, а также передает ряд своих выводов в практику выполнения технических чертежей, обеспечивая их выразительность и точность.
Правила построения изображений в начертательной геометрии основаны на методе проекций.
Рассмотрение метода проекций начинают с построения проекций точки, так как любая пространственная форма рассматривается как ряд точек.
Проекции центральные
При центральном проецировании задаётся плоскость проекций (обозначается строчными буквами греческого алфавита 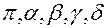 и другими ) и центр проекций – точка (обозначается прописными буквами латинского алфавита – A, B, … S и т.д.), не лежащая в данной плоскости (рис.1.).
и другими ) и центр проекций – точка (обозначается прописными буквами латинского алфавита – A, B, … S и т.д.), не лежащая в данной плоскости (рис.1.).
Взяв некоторую произвольную точку в пространстве (например (∙) А), проведем через неё и центр проекций S прямую до пересечения с
плоскостью проекций  0. Получим А0 – проекцию точки А на плоскость
0. Получим А0 – проекцию точки А на плоскость  0. Так же поступим с произвольными точками в пространстве В и С.
0. Так же поступим с произвольными точками в пространстве В и С.
В0, С0 - центральные проекции (∙) В и (∙) С на плоскость  0.
0.

Но в данном случае, имея проекцию точки, нельзя однозначно определить положение самой точки в пространстве, так любая точка, лежащая на проецирующей прямой SA, проецируется в А0. Для единственного решения необходимы дополнительные условия.
Проекции параллельные
Если принять, что центр проекций бесконечно удалён от плоскости проекций, то проецирующие прямые будут параллельны между собой. Для их проведения должно быть указано некоторое направление (рис.2).
 | |||
| |||
Следовательно, параллельной проекцией точки называется точка пересечения проецирующей прямой, проведенной параллельно заданному направлению, с плоскостью проекций.
Существуют правила, распространяющиеся как на центральное проецирование, так и на параллельное:
1. Для прямой линии проецирующей поверхностью в общем случае служит плоскость, потому прямая проецируется в виде прямой;
2. Каждая точка и линия в пространстве имеют единственную свою проекции;
3. Каждая точка на плоскости может быть проекцией множества точек;
4. Каждая линия на плоскости может быть проекцией множества линий;
5. Для построения проекций прямой достаточно спроецировать две её точки;
6. Если прямая параллельна направлению проецирования, то её проекция является точкой;
7. Отрезок прямой, параллельный плоскости проекций, проецируется в натуральную величину.
Метод Монжа
Метод параллельного ортогонального проецирования был развит в трудах французского учёного Монжа.
Гаспар Монж (1746-1818) – крупный геометр и государственный деятель периода правления Наполеона. Его труд по начертательной геометрии долго не публиковался, так как имел большое практическое значение для выполнения чертежей военных объектов, и увидел свет только в конце 18 века. Изложенный Монжем метод параллельного ортогонального (т.е., прямоугольного) проецирования до сих пор остается основным методом составления технических чертежей, обеспечивая выразительность, точность и удобоизмеримость предметов на плоскости.
Дата: 2019-03-05, просмотров: 358.