Перпендикуляр к плоскости перпендикулярен к любой прямой в этой плоскости. Но чтобы прямая являлась перпендикуляром к плоскости, она должна быть перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

    Чтобы проекция перпендикуляра к плоскости была перпендикулярна прямой в плоскости эта прямая должна быть горизонталью или фронталью (см. теорему о проецировании прямого угла). Поэтому для построения перпендикуляра берут две прямые: горизонталь и фронталь.

    Итак: у перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция перпендикулярна к фронтальной проекции фронтали (рис.41).

Рис. 41 Перпендикуляр к плоскости, заданной треугольником

    Следы плоскости можно считать нулевой фронталью и горизонталью. Следовательно, если плоскость задана следами, то:

горизонтальная проекция перпендикуляра к плоскости перпендикулярна горизонтальному следу плоскости, а фронтальная – фронтальному следу плоскости (рис.42).

Рис. 42 Перпендикуляр к плоскости, заданной следами

Взаимное положение плоскостей

Две плоскости относительно друг друга могут располагаться следующим образом:

1) быть параллельными между собой;

2) пересекаться.

Параллельные плоскости

    Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны между собой.

Рис. 43 Плоскости, параллельные между собой

Пример:  

Дана плоскость, треугольник АВС. Через точку М провести плоскость β, параллельную заданной. Через заданную точку М проведем две пересекающиеся прямые (рис.43), которые определяют собой искомую плоскость β, параллельные сторонам треугольника АВС:  MN║АВ, МК║ВС.

Если два пересекающихся между собой следа одной плоскости параллельны двум пересекающимся следам другой плоскости, то эти плоскости параллельны (рис.44).

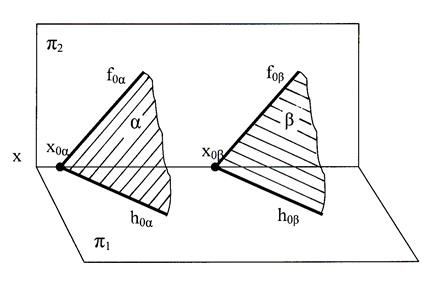
Рис. 44 Параллельные плоскости общего положения,

 заданные следами

Если параллельны не пересекающиеся следы, надо построить профильные следы (рис.45) и по их положению определить взаимное положение плоскостей.

а)                                                б)

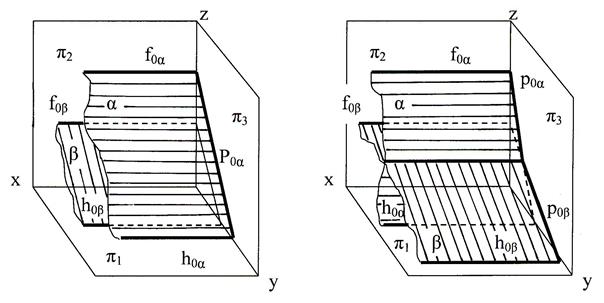
Рис. 45 Профильно-проецирующие плоскости:

а) параллельные; б) пересекающиеся

Пересекающиеся плоскости

Если хотя бы одна пара следов пересекается, то плоскости пересекаются.

Линия пересечения двух плоскостей вполне определяется двумя точками, каждая из которых принадлежит обеим плоскостям (рис.46).  MN – линия пересечения плоскостей общего положения α и β, где точки  М и N являются следами линии пересечения.

Если одна из плоскостей проецирующая (в данном случае плоскость α – горизонтально-проецирующая), то линия пересечения очевидна – это линия 1-2 (рис.47).

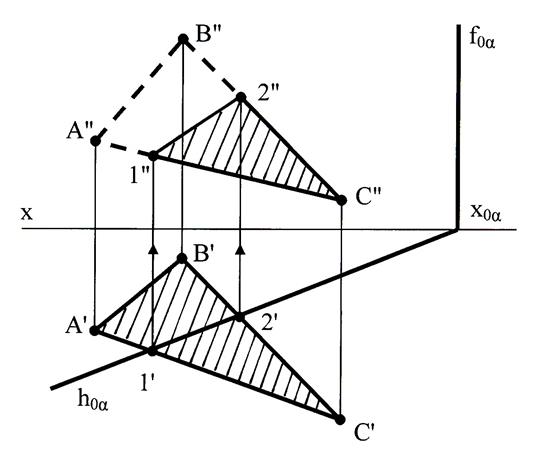
Рис.47 Пересечение треугольника

горизонтально-проецирующей плоскостью

Если одна из плоскостей плоскость β параллельна плоскости ₁ (рис.48), т.е. горизонтальная, а вторая плоскость общего положения α, то линией их пересечения будет горизонталь МN.

а)                                                         б)

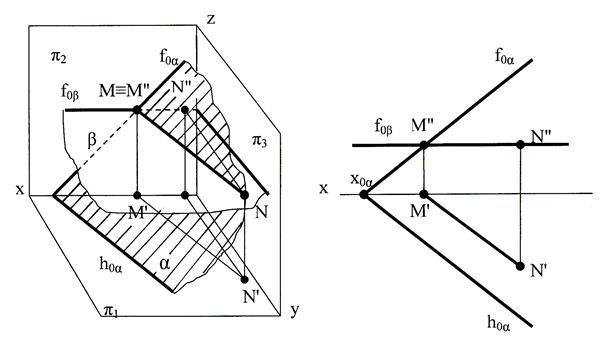
Рис. 48 Пересечение плоскости общего положения с горизонтальной плоскостью: а) в аксонометрической проекции; б) на эпюре

Теперь рассмотрим случай построения линии пересечения двух плоскостей, когда одна из плоскостей α задана следами, а другая β – треугольником АВС. Построение показано на рис.49. Для определения положения линии пересечения К₁  и К₂  заданных плоскостей возьмём две вспомогательные горизонтальные плоскости (γ₁ и γ₂), пересекающие каждую из плоскостей α  и β. При пересечении заданных плоскостей плоскостью γ₁  получаем прямые с проекциями А'1', А"1", и h₁' , h₁^".

Эти прямые, расположенные в плоскости γ₁, в своём пересечении определяют первую точку К₁ линии пересечения плоскостей α и β.

Введя далее плоскость γ₂ , получаем в её пересечении с плоскостями α и β прямые с проекциями 2^'3', 2"3" и h₂', h₂". Эти прямые, расположенные в плоскости γ₂, в своём пересечении определяют вторую точку К₂, общую для α и β. Таким образом определена линия пересечения (К₁^'К₂^' – её горизонтальная проекция, К₁^"К₂^" – её фронтальная проекция) заданных плоскостей α и β.

Рис. 49 Построение линии пересечения плоскостей

Построение линии пересечения двух плоскостей по точкам пересечения прямых линий с плоскостью приведено на рис. 50. В качестве плоскостей фигурируют треугольники АВС и DEF.

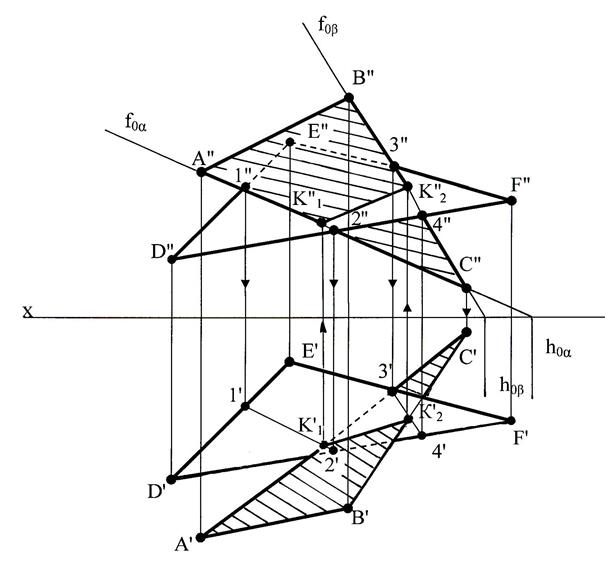
Рис. 50 Пересечение треугольников

Прямая К₁К₂ построена по точкам пересечения сторон АС и ВС треугольника АВС с плоскостью треугольника DEF. Вспомогательная фронтально-проецирующая плоскость α, проведённая через АС, пересекает треугольник DEF по прямой с проекциями 1"2" и 1'2'. В пересечении проекций 1'2' и А'С' получена горизонтальная проекция К₁^'. Затем построена К₁^". Аналогичным образом, используя вспомогательную фронтально-проецирующую плоскость β, найдены проекции точки К₂^', К₂^". Видимость треугольников определена методом конкурирующих точек.