Предположим, что в пространстве имеется отрезок общего положения АВ (рис. 19).

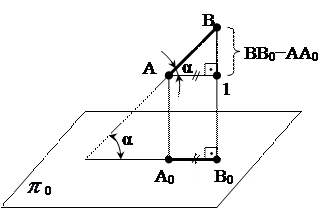
Рис. 19 Метод прямоугольного треугольника

в аксонометрической проекции

Опустив из точек А и В перпендикуляры на плоскость проекций ₀, найдем его проекцию на эту плоскость А₀В₀. Выполнив дополнительное несложное построение, получим прямоугольный треугольник АВ1, у которого гипотенуза является истинной величиной отрезка, один из катетов (А1) равен проекции отрезка на плоскость ₀, а второй (В1) равен разности расстояний концов отрезка от плоскости проекций.

Угол прямой линии с плоскостью проекций (α), определяется как угол, составленный прямой с её проекцией на этой плоскости.

Предположим, на эпюре (рис. 20) задана прямая общего положения АВ, своими проекциями А'В' – горизонтальной, А"В" – фронтальной.

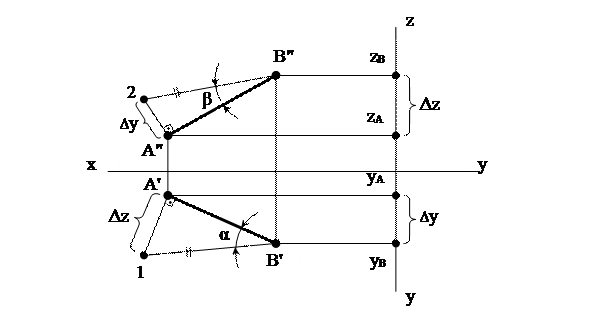
Рис. 20 Определение натуральной величины отрезка AB

     Для определения натуральной величины этого отрезка построим прямоугольный треугольник А'В'1, приняв за один из катетов горизонтальную проекцию прямой А'В', в качестве другого величину ∆Z – разность расстояний концов отрезка до горизонтальной плоскости проекций. Тогда, гипотенуза этого треугольника В'1 будет представлять собой натуральную величину отрезка. Угол α – угол наклона прямой АВ к горизонтальной плоскости проекций 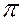₁. Аналогичное построение выполнено на фронтальной проекции. Разность расстояний концов отрезка до плоскости 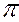₂  определит величина ∆у. β – угол между прямой и фронтальной плоскостью проекций.

Проекция плоскости. Следы плоскости

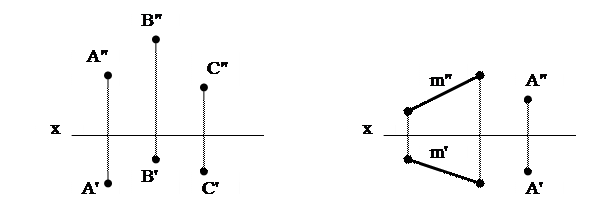
     Положение плоскости в пространстве определяется, а в соответствии с этим может быть задана (Рис.21):

а) проекциями трёх точек, не лежащих на одной прямой;

б) проекциями прямой и точки вне прямой;

в) проекциями пересекающихся прямых;

г) проекциями параллельных прямых.

   а)                                                            б)     

   в)                                                            г)     

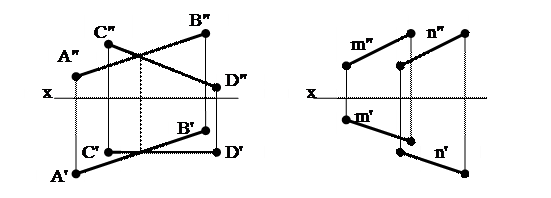
Рис 21. Задание плоскости на эпюре: а) проекциями трёх точек;

б) проекциями прямой и точки вне прямой; в) проекциями пересекающихся прямых; г) проекциями параллельных прямых

Следы плоскости

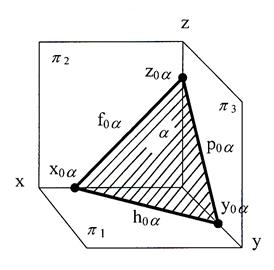
     Более наглядно плоскость может быть задана следами.

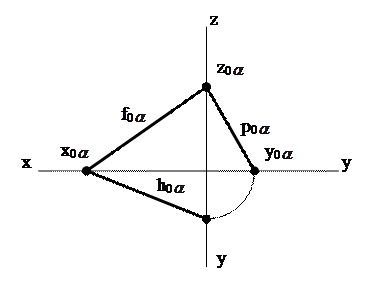
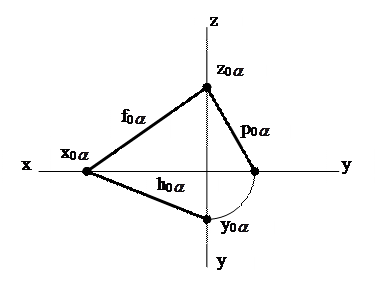
     Следы плоскости – это линии, по которым плоскость пересекается с плоскостями проекций. На чертеже они обозначаются следующим образом: h₀ 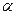 - горизонтальный след плоскости; f₀  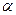- фронтальный и p₀  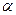- профильный (рис.22).

а)	б)
Рис. 22 Следы плоскости общего положения: а) в аксонометрической проекции; б) на эпюре

     Плоскость, заданную любым из перечисленных выше способов, можно преобразовать в плоскость, заданную следами.

     Предположим, плоскость β задана пересекающимися прямыми (рис.23). Для построения прямой, по которой плоскость β пересечет горизонтальную плоскость проекций 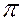₁ (т.е. горизонтального следа плоскости h_0β), достаточно найти две точки, которые одновременно принадлежали бы плоскости β и плоскости 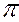₁. Такими точками будут горизонтальные следы прямых m и n, соответственно Н _m , Н_n.

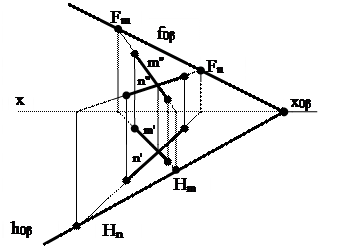
Рис. 23 Преобразование плоскости, заданной пересекающимися прямыми, в плоскость, заданную следами

Соединив точки Н_m и Н_n  получим горизонтальный след плоскости h_0β. Для построения фронтального следа плоскости найдём фронтальный след прямой  m - F_m и фронтальный след прямой n - F_n. Соединив полученные точки (F_m  и F_n), получим фронтальный след плоскости f_0β.

х_0β – точка пересечения следов (f₀  и f_0β ) на оси Х, называемая точкой схода следов.

Угол между следами на чертеже не равен углу между следами в пространстве ( это видно из рассмотрения трёхгранного угла на рис.22).

Плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций называется плоскостью общего положения (рис.22, 23).