Ряд распределения – ряд величин характеризующих состав изучаемых явлений по одному признаку.
Ряды распределения бывают двух видов:
1. атрибутивные – образованные по качественному признаку.
2. вариационные - образованные по количественному признаку.
Вариационные ряды бывают:
- дискретные (прерывные) т.е. принимающие только определённые значения.
Дискретные ряды расположенные в порядке возрастания от наименьшего значения к наибольшему, называются ранжированными.
- непрерывные или интервальные – могут принимать любое значение в пределах интервала.
Вариационные ряды состоят из двух элементов:
3. варианта (х) – числовые значения количественного признака. Они могут быть положительные и отрицательные, абсолютные и относительные.
4. частота (f) – численность отдельных вариантов, показывающая, как часто встречаются те или иные варианты в ряду распределения.
Сумма частот называется объёмом совокупности и определяет число элементов всей совокупности (N).
Частота выражается в виде относительных величин (проценты, доли от единицы), называется частостью (d) и определяется, как отношение частоты к объёму совокупности.
2
Для наглядного представления вариационных рядов используют графические методы.
Дискретные ряды представляются в виде полигона распределения – это ломаная кривая по оси х откладываются по значению признака, а по оси у – частоты.
Интервальные ряды – представляются в виде гистограммы распределения (столбиковая диаграмма).
Статистические показатели.
Абсолютные и относительные величины статистики.
3. Абсолютные величины и их виды.
4. Относительные величины и их виды.
1
Показатели, с помощью которых статистика характеризует совокупности единиц в целом и по группам называется обобщающими показателями. К ним относят абсолютные, относительные и средние величины.
Первоначальным видом обобщающим показателей являются абсолютные величины. Их получают в результате статистического наблюдения. Сводки или суммирования первичного статистического материала или расчётным путём, таким образом, абсолютные величины характеризуют численность совокупности и объём изучаемого явления. Все абсолютные величины являются, именованы числами, т.е. имеют единицы измерения.
Виды единиц измерения:
4. Натуральные – применяются тогда, когда единицы измерения соответствуют потребительским свойствам продукта. Единица измерения могут быть простыми и сложными.
5. Стоимостные – получаются умножения количества единиц на цену единицы.
6. Условно-натуральные – применяются, если разновидности продукции обладают общностью одного потребительского свойства.
Абсолютные величины могут быть индивидуальными и суммарными.
2
Относительные величины – характеризуют количественное соотношение сравниваемых абсолютных величин и представляют собой частное от деления двух статистических величин:
В числителе всегда находится сравниваемая величина (то, что сравнивают), а в знаменателе база сравнения, то с чем сравнивают.
Форма выражения относительных величин:
5. Коэффициенты (доли). База сравнения принимается за единицу.
6. Проценты. База сравнения принимается за сто.
7. Промилле. База сравнения принимается за тысячу (%0).
8. Продецимилле. База сравнения принимается за 10.000 (%00).
Виды относительных величин:
8. Относительные показатели планового задания - отношение уровня запланированного на предстоящий период к уровню показателя достигнутого в предыдущем периоде.
9. Относительный показатель выполнения плана – отношение фактически достигнутого уровня в текущем периоде к уровню планируемого показателя на этот же период.
10. Относительные показатели динамики характеризуют изменения уровня развития какого-либо явления во времени.
11. Относительные показатели структуры характеризуют состав изучаемой совокупности, доли или удельные веса элементов совокупности в общем итоге и представляют собой отношение части единиц совокупности ко всему объёму совокупности.
12. Относительные показатели интенсивности – характеризуют степь развития данного явления в определённой среде и могут выражаться в кратных отношениях, в процентах и промилле.
13. Относительные показатели координации характеризуются отношением частей совокупности к одной из них принятой за базу сравнения, она показывает во сколько раз одна часть совокупности больше другой, или сколько единиц одной части совокупности приходится на одну, десять, сто или тысячу единиц другой части.
14. Относительные показатели сравнения – характеризуют отношение одноимённых абсолютных показателей, соответствующих одному и тому же периоду или моменту времени, но к различным объектам или территориям.
Средние величины в статистике
4. Понятие и виды степенных средних величин.
5. Структурные средние величины.
6. Показатели вариации.
1
Средняя величина – обобщающая характеристика изучаемого признака, отражающая его типичный уровень в расчёте на единицу совокупности в конкретных условиях места и времени.
Средние величины – это общая характеристика совокупности по количественному признаку, показывающему уровень признака, которая относится ко всей совокупности.
Основным условием научного использования средней величины является качественная однородность совокупности. Средние величины являются именованными числами и имеют ту же размерность, что и признак у отдельных единиц совокупности.
Средние величины могут быть:
· общими – рассчитанные по совокупности в целом
· групповыми – исчисленные для каждой группы
Виды средних величин
1. Степенные средние величины
В основе их расчета лежит общая формула: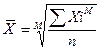 
,
если m = 1 – средняя арифметическая
m = -1 – средняя геометрическая
m = 0 – средняя геометрическая
m = 2 – средняя квадратическая
m = 3 – средняя кубическая
У степенных средних есть свойство возрастать с повышением степеней (показателя), которое называется правилом мажорантности средних.
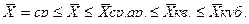
Степенные средние величины могут быть простыми и взвешенными.
2.Структурные средние величины: мода и медиана
1.1 Средняя арифметическая – применяется в тех случаях, когда объем варьирующего признака для всей совокупности является сумма значений признаков отдельных ее единиц.
Средняя арифметическая простая
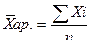
Средняя арифметическая взвешенная
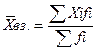
Пример: Вычислить средний стаж 10 работников по данным: 6.5.4.3.3. 4.5.4.5.4.
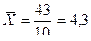лет (простая); 
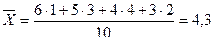лет(взвешенная)
Средняя арифметическая обладает некоторыми свойствами:
1) Если значение признака каждой единицы совокупности уменьшить или увеличить на одну и ту же величину А, то со средней произойдут те же изменения.
2) Если значение признака каждой единицы умножить или разделить на постоянное число А, то средняя арифметическая уменьшится или увеличится в А раз.
3) Если частоту каждого значения признака уменьшить или увеличить в n раз, средняя арифметическая не изменится.
Эти свойства используются для упрощения расчетов средней « способом моментов»
Для этого выбирается значение признака обладающего наибольшей частотой.
Пример: Рассчитаем среднюю арифметическую «способом моментов» по следующим данным:
Таблица 1 - Распределение предприятий по стоимости ОПФ:
| Группы предприятий по стоимости ОПФ млн. руб. | Число предприятий f | Серединный интервал, x |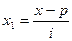 
| 
|
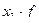
| 14-16 | 2 | 15 | -2 | -4 |
| 16-18 | 6 | 17 | -1 | -6 |
| 18-20 | 10 | 19 | 0 | 0 |
| 20-22 | 4 | 21 | 1 | 4 |
| 22-24 | 3 | 23 | 2 | 6 |
| Итого: | 25 | – | 0 | 0 |
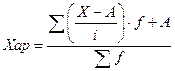
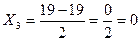
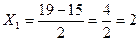
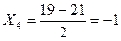
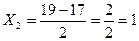
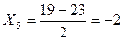
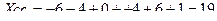
1.2 Средняя гармоническая – величина обратная средней арифметической, применяется, когда статистическая информация не содержит частоты по отдельным вариантам совокупности, а представлена, как их произведение, или при расчете общей средней из среднегрупповых.
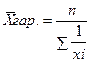- простая
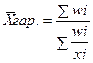- взвешенная
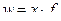- вес средней
Пример: Определить среднюю цену на товар по следующим данным.
Таблица 2 - Цена и сумма реализации на товары по трем городам
| Город | Цена, тыс.руб. (х) | Сумма реализации тыс./руб. (w) | Количество реализованных ед. кг. (f) |
| А | 30 | 600 | 20 |
| В | 20 | 1000 | 50 |
| С | 25 | 350 | 14 |
| Итого: | 75 | 1950 | 84 |
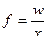
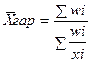
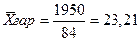тыс. руб.
1.3 Средняя геометрическая - применяется при расчетах средних относительных величин динамики (цепных), т.е. характеризует средний коэффициент роста.
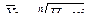- простая 
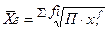- взвешенная
Пример: Темп роста товарооборота по годам составил:
1997г. – 1,053 1999г. – 1,049
1998г. – 1,051 2000г. – 1,058
Определить средний темп роста.
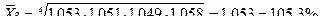
Ответ: средний темп роста т/о составил по годам (1987 – 1990г.) – 105,3%, а средний прирост составил 5,3%
Так же средняя геометрическая может применяться для определения равноудаленной величины от максимального и минимального значения признака.
Пример: Страховая сумма выплат по страховке может изменится от 100 000 до 10 000 руб. в год. Определить среднюю сумму выплат.
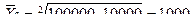руб.
Ответ: Средняя сумма выплат (страховых) в год составляет 1000 рублей.
1.4 Средняя квадратическая – используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической.
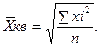- простая 
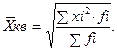- взвешенная
1.5. Средняя кубическая
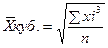- простая 
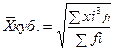- взвешенная
Применение этих величин ограничено: если средний размер признака представлен в квадратных или кубических единицах измерения.
2.
Структурные средние величины применяются для изучения внутреннего строения и структуры рядов распределения значений признака.
К ним относится:
2.1Мода – наиболее часто встречающиеся значение признака, т.е. имеющее наибольшую частоту. В интервальном ряду с равными интервалами, мода вычисляется по формуле.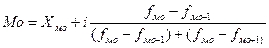 
xмо – начало модального интервала, нижняя граница
i – величина модального интервала
fмо – частота в модальном интервале
fмо-1 – частота предмодального интервала
fмо+1 –частота послемодального интервала
2.2.Медиана – это вариант, который находится в середины вариационного ряда и делит его на две равные части. Для определения медианы вариационного ряда, необходимо его проранжировать и найти порядковый номер медианы.
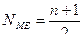NМЕ – порядковый номер медианы
Рассмотрим пример со стажем (лет)
3, 3, 4, 4, 4, 4, 5, 5, 5, 6.
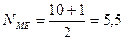
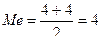
Ответ: Половина работников имеет стаж менее 4 лет, а половина более 4 лет.
Медиана, в интервальных рядах, рассчитывается по формуле
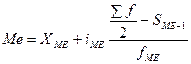
Xме – начало медианного интервала
Sме-1 – сумма накопленных частот ряда, предшествующих медианному интервалу.
Медианным считается тот интервал, в котором накопленная частота превышает половину суммы всех частот.
3.
Показатели вариации характеризуют колеблемость отдельных значений признака. К ним относится:
1. Абсолютные показатели
1.1 размах вариации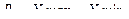 
1.2 Среднее линейное отклонение
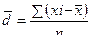для не сгруппированных
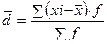для сгруппированных
1.3 Дисперсия – средняя из квадратов отклонений вариантов значений признака от их средней величины
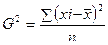для не сгруппированных
для сгруппированных
1.3 Среднее квадратическое отклонение
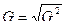
Дисперсия обладает некоторыми свойствами:
1 Дисперсия постоянной величины равна нулю
2 Если все варианты значений признака уменьшить на одно и то же число, то дисперсия не изменяется.
3 Если все варианты значения признака уменьшится в К раз, то дисперсия уменьшится К2 раз.
2. Относительные показатели вариации
2.1 Относительный размах вариации
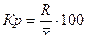
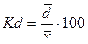
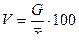V – коэффициент вариации
Виды и методы анализа рядов динамики
4. Понятия и виды рядов динамики.
5. Показатели рядов динамики.
6. Средние показатели рядов динамики.
1
Ряд динамики (временной) – ряд расположенный в хронологической последовательности статистических показателей.
Каждый ряд динамики состоит из двух элементов:
1) период времени к которому относятся статистические показатели.
2) Статистические показатели характеризующие изучающий объект (уровень ряда).
Статистические показатели могут быть представлены абсолютными, относительными и средними величинами.
Существует два способа сопоставления уровней ряда
3. Если каждый уровень сравнивается с одним и тем же предшествующим, то это сравнение с постоянной базой и получаемые показатели называются базисными.
4. Если каждый уровень ряда сравнивается с непосредственно ему предшествующим, т.е. с переменной базой, то получаемые показатели называются цепными.
2
Дата: 2019-03-05, просмотров: 239.
