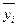На основе характеристик выборочной совокупности получить достоверные данные о показателях в генеральной совокупности.
По виду различают индивидуальный отбор (отбираются отдельные единицы совокупности);
Групповой отбор – отбираются качественно однородные группы или серии;
Комбинированный отбор – смежные первый и второй отбор.
Основные характеристики генеральной и выборочной совокупностей:
N – объём генеральной совокупности
n – объём выборки
x – генеральная средняя
x – выборочная средняя
p генеральная доля
w – выборочная доля
G2 – генеральная дисперсия
S2 – выборочная дисперсия
G – среднее квадратическое отклонение генеральной совокупности
S – среднее квадратическое отклонение выборки
Характеристики выборочной совокупности:
Средняя выборочная ( ) и выборочная доля (w) отличается от генеральной совокупности на величину ошибки выборки для различных видов выборки и методов отбора.
2
Существует два метода отбора:
- Повторная выборка – общая численность единиц генеральной совокупности в процессе выборки остаётся неизменной.
- Бесповторная выборка – единица совокупности попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшей выборке не участвует.
Виды выборки:
1) Собственно-случайная и механическая выборка. В данном случае предельная ошибка для средней и для доли при повторном отборе определяется по формулам:
При бесповторном отборе эти показатели определяются по формулам:
2) Типическая выборка- генеральная совокупность разбивается на однородные типические группы.
Предельная ошибка рассчитывается по формулам:
3) Серийная выборка – генеральную совокупность делят на финансовые по объёму группы – серии. Внутри серий проводится сплошное наблюдение единиц попавших в серию.
Предельные ошибки выборочной средней и доли определяются по формулам:
Часто возникает необходимость в определении численности выборки.
При случайном повторном отборе:
При случайном бесповторном и механическом отборе:
В практике проектирования выборочного наблюдения возникает потребность в нахождении численности выборки, которая необходима для обеспечения определённой точности расчёта генеральных характеристик: средней и доли
При случайном повторном отборе, численность выборки определяется по формуле:
При случайном бесповторном и механическом отборе численность выборки определяется по формуле:
Для типической выборки
Для серийной выборки
Тема 8
План:
- Общие понятия о статистических связях
- Методы выявления наличия корреляционной связи
- Уравнения регрессии
1
Между различными статистическими показателями существует определенная связь. Она выявляется с помощью методов статистики и математики.
Существуют различные типы связей между явлениями:
1. По характеру зависимости:
- Функциональные связи – характеризуются полным соответствием между изменением факторного признака и изменением результативной величины. При этом каждому значению признака фактора соответствует вполне определенное значение результативного признака. У=f(x)
- Корреляционные связи – изменение результативного признака обусловлено влиянием факторного, не всецело, а лишь частично, т.к. возможно влияние прочих факторов. У=f(x)+Е
2.По направлению:
- Прямая связь, при которой с ростом значений факторного признака растут значения результативного признака
- Обратная связь, при которой с увеличение значений одного признака, величина другого уменьшается
3. По аналитическому выражению:
- Линейные - выражаются аналитическим уравнением прямой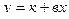 
Криволинейные - выражаются уравнением гиперболы, параболы, показательной, степенной, логарифмической функцией и др.
гиперболическая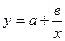 
показательная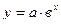 
параболическая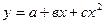 
степенная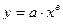 
логарифмическая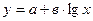 
Параметр в называется коэффициентом регрессии и показывает на сколько в среднем меняется величина результативного признака У при изменении факторного признака (Х) на единицу..
При наличии прямой зависимости В > 1, а обратной В < 1.
2.
Для определения наличия корреляционной связи применяется ряд специфических методов:
1. Метод парной корреляции, т.е. сопоставление 2-х параллельных рядов: ряда значений факторного признака (х) и соответствующего ему значения результативного признака (у).Для установления данной зависимости необходимо ранжировать ряд значений факторного признака.
Если возрастание величины факторного (x) признака влечет за собой возрастание величины результативного (у) говорят, о возможном наличии прямой корреляционной связи, если к уменьшению, то об обратной корреляционной связи.
2.Метод построения групповой или корреляционной таблиц, применяется в случае наличия большого числа различных значений результативного признака, соответствующих одному и тому же значению факторного признака
3. Графический метод – используется для предварительного выявления наличия связи и выбора формы связи. Если линия приближается к прямой, то можно предположить наличие корреляционной связи.
Рассмотрим установление наличия корреляционной связи перечисленными методами на условном примере.
По 20 туристическим фирмам были установлены затраты на рекламу (факторный признак, Х) и количество туристов, воспользовавшихся услугами каждой фирмы (результативный признак У)
| №фирмы | Затраты на рекламу,у.е. | Количество туристов | Знаки отклонений | Совпадения (А) Несовпадения (Б) | |
| х | у | ||||
| 1 | 8 | 800 | - | - | А |
| 2 | 8 | 850 | - | - | А |
| 3 | 8 | 720 | - | - | А |
| 4 | 9 | 850 | - | - | А |
| 5 | 9 | 800 | - | - | А |
| 6 | 9 | 880 | - | - | А |
| 7 | 9 | 950 | - | - | А |
| 8 | 9 | 820 | - | - | А |
| 9 | 10 | 900 | + | - | Б |
| 10 | 10 | 1000 | + | + | А |
| 11 | 10 | 920 | + | - | Б |
| 12 | 10 | 1060 | + | + | А |
| 13 | 10 | 950 | + | - | Б |
| 14 | 11 | 900 | + | - | Б |
| 15 | 11 | 1200 | + | + | А |
| 16 | 11 | 1150 | + | + | А |
| 17 | 11 | 1000 | + | + | А |
| 18 | 12 | 1200 | + | + | А |
| 19 | 12 | 1100 | + | + | А |
| 20 | 12 | 1000 | + | + | А |
По представленному в порядке возрастания факторному признаку и соответствующему ему результативному признаку можно предположить наличие прямой корреляционной связи. Однако, в некоторых вариантах есть и обратное соотношение (фирма 11).Это говорит о том, что на величину результативного признака влияют прочие факторы.
Построение корреляционной таблицы начинают с группировки факторного и результативного признаков. Для факторного признака число групп составит пять. Для результативного признака определим величину интервала по формуле Стэрджесса: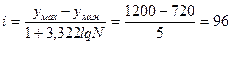 
чел.
В корреляционной таблице факторный признак располагают в строках, а результативный - в столбцах таблицы.
| Середина интервала,у | 768 | 864 | 960 | 1056 | 1152 | fх |
|
| Группы по х и у | 720-816 | 816-912 | 912-1008 | 1008-1104 | 1104-1200 | ||
| 8 | 2 | 1 | 3 | 800 | |||
| 9 | 1 | 3 | 1 | 5 | 864 | ||
| 10 | 1 | 3 | 1 | 5 | 960 | ||
| 11 | 1 | 1 | 2 | 4 | 1032 | ||
| 12 | 1 | 1 | 1 | 3 | 1056 | ||
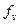
| 3 | 6 | 6 | 2 | 3 | 20 |
Если частоты расположены на диагонали из левого верхнего угла в правый нижний угол, то можно предположить наличие прямой корреляционной зависимости, если справа налево, то об обратной. Для более точного установления наличия связи необходимо рассчитать средние значения результативного признака.
Среднее число туристов для каждой группы определяется по формуле средней арифметической взвешенной:
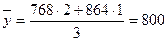чел и т. д.
По средним значениям результативного признака свидетельствует о возможном наличии прямой корреляционной зависимости числа туристов от затрат на рекламу.
Построение групповой таблицы.
Все единицы совокупности разбиваются на группы в зависимости от величины признака – фактора и по каждой группе вычисляются средние значения результативного признака.
| Группы туристических фирм по затратам на рекламу, у.е. | Число фирм в группе | Среднее число туристов, воспользовавшихся услугами фирм, человек |
| 8 | 3 | 790 |
| 9 | 5 | 860 |
| 10 | 5 | 966 |
| 11 | 4 | 1063 |
| 12 | 3 | 1100 |
| Итого | 20 |
Увеличение среднего числа туристов свидетельствует о наличии прямой корреляционной связи.
Также для предварительного выявления наличия связи и определения её характера применяют графический метод.
Полученный график называется полем корреляции, на котором также строится эмпирическая линия связи по средним значениям показателя.
3
Охарактеризовать зависимость результативного признака от факторного можно с помощью показателей тесноты связей:
– коэффициент корреляции знаков
– линейный коэффициент корреляции
– коэффициент детерминации
Наиболее простым показателем тесноты связи является коэффициент корреляции знаков (Фехнера)
Для этого необходимо рассчитать среднее значение х (9,95) и у (952) и сравнить каждое значение признака со средним. Посчитав число совпадений и несовпадений знаков, определяется коэффициент Фехнера, который может принимать значения от -1 до +1. Чем ближе к -1, тем ярче выражена обратная связь, чем ближе к +1 - обратная.
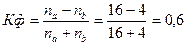
Полученный коэффициент свидетельствует о наличие прямой корреляционной связи.
Более совершенным показателем является линейный коэффициент корреляции.
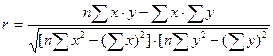
Данный коэффициент также может принимать значения от -1до +1. Чем ближе значение к единице, тем теснее связь между признаками.
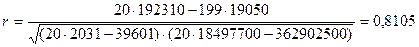
Квадрат коэффициента корреляции носит название коэффициента детерминации. Для рассматриваемого примера его величина составляет 65,69 %, т.е. 65,69% числа клиентов, воспользовавшихся услугами фирмы, объясняется затратами на рекламу своих услуг.
Коэффициент эластичности – показывает, на сколько % изменяется величина результативного признака при изменении факторного признака на 1%
Дата: 2019-03-05, просмотров: 283.
