Выборочное наблюдение — это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность.
Совокупность, из которой производится отбор, называется генеральной, а совокупность отобранных единиц называется выборочной. Характеристики выборочной совокупности:
Средняя выборочная (х) и выборочная доля (г) отличается от генеральной совокупности на величину ошибки выборки для различных видов выборки и методов отбора.
Существует два метода отбора:
Повторная выборка — общая численность единиц генеральной совокупности в процессе выборки остаётся неизменной.
Бесповторная выборка — единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшей выборке не участвует.
Виды выборки:
1 .Собственно-случайная и механическая выборка. В данном случае предельная ошибка для средней и для доли при повторном отборе определяется по формулам (8,9,10)
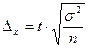 (8)
(8)
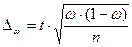 (9)
(9)
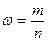 (10)
(10)
где 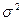 -дисперсия выборочной совокупности;
-дисперсия выборочной совокупности;
п —численность выборки;
t —коэффициент доверия, m -доля единиц, обладающих признаком,
N —численность генеральной совокупности
2.При бесповторном отборе эти показатели определяются по формулам(11,12)
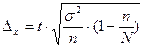 (11)
(11)
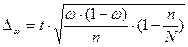 (12)
(12)
З.Типическая выборка- генеральная совокупность разбивается на однородные типические группы.
Предельная ошибка рассчитывается по формулам(13,14)
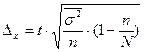 (13)
(13)
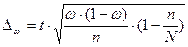 (14)
(14)
4.Серийная выборка — генеральную совокупность делят на одинаковые по объёму группы — серии. Внутри серий проводится сплошное наблюдение единиц попавших в серию.
Предельная ошибка выборочной средней и доли определяется по формуле (15)
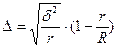 , (15)
, (15)
где 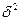 - межсерийная дисперсия;
- межсерийная дисперсия;
R —число серий в генеральной совокупности,
г —число отобранных серий
Часто возникает необходимость в определении численности выборки.
При случайном повторном отборе: 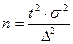 (16)
(16)
При случайном бесповторном и механическом отборе: 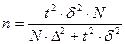 (17)
(17)
Для типической выборки: 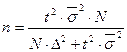 (18)
(18)
Для серийной выборки: 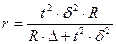 (19)
(19)
Тема З Ряды динамики
Ряд расположенных в хронологической последовательности значений статистической деятельности показателей представляет собой временной ряд или ряд динамики.
Каждый ряд динамики состоит из 2-х элементов:
— период времени, к которому относятся статистические данные
— статистические показатели, характеризующие изучаемый объект (уровень ряда)
Виды рядов динамики
— Интервальные — характеризуют уровень динамического ряда за определенный промежуток времени
— Моментный — характеризуют уровень динамического ряда на определенную дату или момент времени.
Если сравнению подлежат несколько последовательных уровней, то возможно два варианта сопоставления:
— с постоянной базой — базисные показатели. Каждый уровень сравнивается с одним и тем же предшествующим
— с переменной базой — цепные показатели. Каждый уровень сравнивается с непосредственно ему предшествующим.
В зависимости от задач исследования могут быть исчислены следующие показатели динамики.
Абсолютный прирост — разность между последующим уровнем ряда и предыдущим.
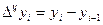
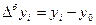 (20)
(20)
Темп роста — отношение уровней ряда динамики последующего предыдущему, выражается в % или коэффициентах.
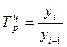
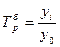 (21)
(21)
Темп прироста Тпр = Тр -1 (22)
Абсолютное значение одного % прироста — это 1/100 часть предыдущего уровня ряда.
Средние уровни ряда:
· для интервального ряда у = 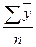 (23)
(23)
· для моментного ряда
— с равными промежутками (по формуле средней хронологической)
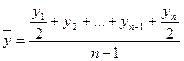 (24)
(24)
— с неравными промежутками (средняя арифметическая взвешенная)
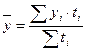 , (25)
, (25)
где t — количество дней между смежными датами
Средние показатели изменения рядов динамики:
средний абсолютный прирост 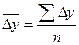 (26)
(26)
средний темп роста 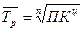 (27)
(27)
средний темп прироста 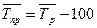 (28)
(28)
среднее абсолютное значение 1% прироста А1% = 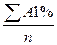 (29)
(29)
На основе базисных темпов роста строится линейный график. На оси абсцисс откладывают периоды времени, а на оси ординат - базисные темпы
роста.
Расчеты показателей рекомендуется представить в табличном виде:
Таблица 2 - Расчет показателей динамики
| Годы
| Уровни ряда | Абсолютный прирост | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста | |||
| цепной | базисный | цепной | базисный | цепной | базисный | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Тема 4 Индексы
Статистические индексы применяются для характеристики сложных социально - экономических совокупностей, состоящих из разнородных, непосредственно несоизмеримых величин.
Индивидуальные индексы — характеризуют изменение только одного элемента совокупности, различают индексы:
цены: 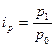 (3О); количества
(3О); количества 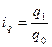 (31); товарооборота
(31); товарооборота 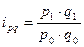 (32)
(32)
Агрегатные индексы характеризуют изменение нескольких элементов совокупности:
Физического объема 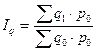 (33)
(33)
Разница между числителем и знаменателем индекса обозначает абсолютное изменение товарооборота за счет изменения физического объема.
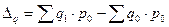 (34)
(34)
Цены и других качественных показателей
Если за базу сравнения принимаются показатели отчетного периода, используются формулы Пааше:
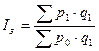 (35)
(35)
Разница между числителем и знаменателем называют абсолютный прирост товарооборота (выручки, продаж) в результате изменения цен или экономию перерасход денежных средств населения в результате среднего снижения (повышения) цен.
Если за базу сравнения применяются показатели базисного периода используют формулы Ласпейреса
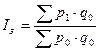 (36)
(36)
Разница между числителем и знаменателем показывает условный абсолютный прирост товарооборота, если бы объем продаж в отчетном и базисном периоде совпали.
Товарооборота (выручки от реализации или продаж)
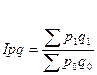 (37)
(37)
Разница между числителем и знаменателем показывает абсолютное изменение товарооборота за счет совместного индекса обоих факторов.
Формулы средних индексов из индивидуальных:
Физического объема: 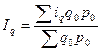 (38)
(38)
Цены: 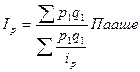 (39)
(39) 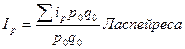 (40)
(40)
Если индексы качественных показателей построены по формулам Пааше, то между индексами существует следующая связь:
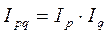 (41)
(41)
На динамику качественных показателей, уровни которых выражены средними величинами, оказывает влияние изменения структуры изучаемого явления. В этом случае применяется индексный метод с использованием системы взаимосвязанных индексов.
1. Индекс переменного состава представляет собой отношение двух взвешенных средних с изменяющимися (переменными) весами.
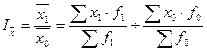 (42)
(42)
2. Индекс постоянного состава — отношение средних взвешенных с одними и теми же весами (при постоянной структуре)
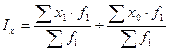 (43)
(43)
3. Индекс структурных сдвигов — характеризуют изменения.
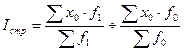 (44)
(44)
Между этими индексами существует следующая взаимосвязь: 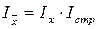 (45)
(45)
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
ВАРИАНТ №1
Задание1. Имеются данные о выпуске продукции по 45 предприятиям (млн. руб.):
| 92 | 101 | 45 | 92 | 98 | 110 | 60 | 46 | 47 | 98 | 107 | 67 | 39 | 44 | 46 |
| 66 | 100 | 104 | 55 | 78 | 47 | 79 | 48 | 54 | 55 | 99 | 56 | 44 | 81 | 48 |
| 99 | 53 | 108 | 48 | 65 | 56 | 100 | 108 | 62 | 75 | 56 | 30 | 50 | 61 | 98 |
Сгруппируйте данные, образовав пять групп с равными интервалами, и определите:
v средний размер выпуска продукции
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v сделайте выводы
Задание 2. В результате опроса методом случайного отбора выяснилось, что 600 человек из 1200 одобрили проводимые мэрией мероприятия. С вероятностью 0,997 определите пределы, в которых находится доля лиц, одобривших мероприятия.
Задание 3.Имеются следующие данные о валовом сборе зерна в одной из областей, млн. т:
| 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| 107 | 103 | 99 | 95 | 89 | 78 | 63 | 69 |
Определите:
v среднегодовое производство валового сбора зерна
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v выявите основную тенденцию валового сбора зерна методом аналитического выравнивания и дайте прогноз валового сбора на 2003год
Задание 4.
Имеются данные о товарообороте магазина и об изменении физического объема товарооборота:
| Товарные группы | Товарооборот, тыс. руб. | Изменение физического объема товарооборота, % | |
| в базисном периоде | в отчетном периоде | ||
| Мука | 1638, 0 | 2517,5 | + 2 |
| Крупа | 187,5 | 270,0 | +20 |
Определите:
v индивидуальный и общий индексы физического объема товарооборота
v общий индекс товарооборота в действующих ценах
v общий индекс цен, используя взаимосвязь индексов
v сумму дополнительных расходов населения при покупке товаров в связи с ростом цен
ВАРИАНТ №2
Задание 1.
Имеются данные о стаже 45 работников одного предприятия (лет):
| 17 | 11 | 12 | 1 | 1 | 12 | 14 | 25 | 3 | 22 | 4 | 17 | 12 | 15 | 16 |
| 15 | 3 | 21 | 10 | 16 | 11 | 8 | 7 | 15 | 20 | 11 | 8 | 4 | 7 | 12 |
| 14 | 2 | 11 | 1 | 23 | 7 | 6 | 4 | 12 | 5 | 6 | 6 | 3 | 10 | 11 |
Осуществите группировку рабочих по стажу, образовав три группы и, охарактеризуйте её следующими показателями:
v средним стажем работы
v дисперсией и средним квадратическим отклонением
v коэффициентом вариации
v модой и медианой
v сделайте выводы
Задание 2.
Для изучения естественной убыли произведено 5% выборочное обследование партии товаров. При этом 10 образцов оказались нестандартными. Определите с вероятностью 0, 997 возможные пределы доли нестандартной продукции.
Задание 3.Имеются следующие данные о конечном потреблении домашних хозяйств в расчете на душу населения в России, руб.
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 6361 | 8888 | 10839 | 12326 | 19617 | 26364 |
Определите:
v среднегодовое значение показателя
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v постройте график динамики базисных темпов исчисленных показателей
Задание 4.
Имеются данные о вкладах населения в Сбербанке:
| Группы населения | Размер вклада, руб. | Удельный вес вкладов в общем числе | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Городское | 500 | 540 | 0,5 | 0,6 |
| Сельское | 420 | 480 | 0,5 | 0,4 |
Определите:
v общие индексы среднего размера вклада для всего населения (переменного, постоянного состава, структурных сдвигов)
v сделайте выводы
ВАРИАНТ №3
Задание 1.
Имеются данные о среднесписочной численности работников 50 предприятий, человек
| 125 | 98 | 456 | 167 | 223 | 213 | 478 | 250 | 134 | 189 |
| 239 | 117 | 360 | 95 | 467 | 98 | 245 | 235 | 213 | 210 |
| 437 | 500 | 111 | 321 | 345 | 458 | 200 | 467 | 321 | 308 |
| 500 | 50 | 134 | 99 | 134 | 367 | 150 | 231 | 235 | 260 |
| 200 | 147 | 256 | 100 | 99 | 106 | 347 | 90 | 478 | 500 |
Осуществите группировку предприятий по среднесписочной численности, образовав пять групп и рассчитайте:
v среднюю численность
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v сделайте выводы
Задание 2.
Какое количество операционистов нужно обследовать в банках региона, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 1 тыс. руб. при среднем квадратическом отклонении заработной платы 5 тыс. руб.
Задание 3.
Имеются данные о динамике численности персонала угольной промышленности России:
| 1998 | 1999 | 2000 | 2001 | 2002 |
| 415 | 370 | 345 | 336 | 295 |
Определите:
v среднегодовое значение показателя
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v выявите основную тенденцию конечного потребления методом аналитического выравнивания и дайте прогноз на 2003год
Задание 4
На основании приведенных данных о реализации продуктов питания рассчитайте:
v агрегатные индексы цен и количества
v агрегатный индекс фактического товарооборота
v сумму дополнительных расходов населения из-за роста цен
|
| Базисный период | Отчетный период | ||
| количество, кг | цена за 1 кг, руб. | количество, кг | цена за 1 кг, руб. | |
| Говядина | 350 | 60 | 470 | 70 |
| Свинина | 400 | 75 | 450 | 80 |
| Баранина | 290 | 55 | 310 | 60 |
ВАРИАНТ №4
Задание 1.
Дата: 2019-03-05, просмотров: 448.