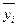ОП 10 СТАТИСТИКА
Профессиональный цикл
Основной профессиональной образовательной программы
по специальности
40.02.01 Право и организация социального обеспечения
для студентов заочной формы обучения
Разработал:
преподаватель
Е.В. Ваниева
Волгоград
АННОТАЦИЯ
Данное методическое пособие предназначено для студентов заочной формы обучения по специальности «Право и организация социального обеспечения» при изучении дисциплины «Статистика».
Рабочая программа учебной дисциплины является частью основной профессиональной образовательной программы в соответствии с ФГОС по специальности СПО 030912 Право и организация социального обеспечения. Рабочая программа составлена для очной и заочной форм обучения.
Место дисциплины в структуре основной профессиональной образовательной программы: общепрофессиональная дисциплина в профессиональном цикле
Цели и задачи дисциплины – требования к результатам освоения дисциплины:
Базовая часть:
В результате освоения дисциплины обучающийся
должен уметь:
-собирать и обрабатывать информацию, необходимую для ориентации в своей профессиональной деятельности;
-оформлять в виде таблиц, графиков и диаграмм статистическую информацию;
- исчислять основные статистические показатели;
-проводить анализ статистической информации и делать соответствующие выводы;
В результате освоения дисциплины обучающийся
должен знать:
-законодательную базу организации государственной статистической отчетности и ответственности за нарушение порядка её представления;
-современную структуру органов государственной статистики;
-источники учета статистической информации;
-экономико – статистические методы обработки учетно – статистической информации;
- статистические закономерности и динамику социально – экономических процессов.
Содержание дисциплины ориентированно на подготовку студентов к освоению профессиональных модулей ОПОП по специальности Право и организация социального обеспечения и овладению профессиональных компетенций (ПК)
ПК 1.1.Осуществлять формирование и хранение дел получателей пенсий, пособий и других социальных выплат.
СОДЕРЖАНИЕ
1.Пояснительная записка----------------------------------------------------------------4
3. Указания по выполнению контрольной работы --------------------------------5
4. Задания для выполнения контрольной работы--------------------------------12
5. Вопросы для самоконтроля и подготовки к зачету---------------------------22
6.Литература---------------------------------------------------- -------------------------23
7. Краткий курс лекций----------------------------------------------------------------24
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Контрольная работа по дисциплине «Статистика» выполняется в сроки, установленные учебным планом.
Работа выполняется одним из следующих способов:
- рукописным в обычных тетрадях;
- на печатных или графических устройствах вывода ЭВМ на листах белой писчей бумаги формата А 4.
Номер варианта контрольной работы должен соответствовать последней цифре зачетной книжки (студенческого билета).
В контрольной работе должны быть представлены: номер варианта, текст задания, подробное решение со ссылкой на формулы и их расшифровка, выводы, таблицы и графики, предусмотренные конкретным заданием.
В конце работы должен быть представлен перечень использованной литературы.
УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Перед выполнением контрольной работы необходимо изучить теоретический материал по темам: «Сводка и группировка статистических данных», «Средние величины и показатели вариации», «Выборочное наблюдение», «Ряды динамики в статистике», «Индексы в статистике».
Тема З Ряды динамики
Ряд расположенных в хронологической последовательности значений статистической деятельности показателей представляет собой временной ряд или ряд динамики.
Каждый ряд динамики состоит из 2-х элементов:
— период времени, к которому относятся статистические данные
— статистические показатели, характеризующие изучаемый объект (уровень ряда)
Виды рядов динамики
— Интервальные — характеризуют уровень динамического ряда за определенный промежуток времени
— Моментный — характеризуют уровень динамического ряда на определенную дату или момент времени.
Если сравнению подлежат несколько последовательных уровней, то возможно два варианта сопоставления:
— с постоянной базой — базисные показатели. Каждый уровень сравнивается с одним и тем же предшествующим
— с переменной базой — цепные показатели. Каждый уровень сравнивается с непосредственно ему предшествующим.
В зависимости от задач исследования могут быть исчислены следующие показатели динамики.
Абсолютный прирост — разность между последующим уровнем ряда и предыдущим.
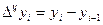
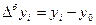(20)
Темп роста — отношение уровней ряда динамики последующего предыдущему, выражается в % или коэффициентах.
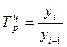
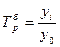(21)
Темп прироста Тпр = Тр -1 (22)
Абсолютное значение одного % прироста — это 1/100 часть предыдущего уровня ряда.
Средние уровни ряда:
· для интервального ряда у =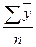 
(23)
· для моментного ряда
— с равными промежутками (по формуле средней хронологической)
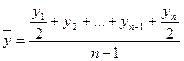(24)
— с неравными промежутками (средняя арифметическая взвешенная)
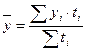, (25)
где t — количество дней между смежными датами
Средние показатели изменения рядов динамики:
средний абсолютный прирост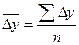 
(26)
средний темп роста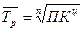 
(27)
средний темп прироста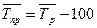 
(28)
среднее абсолютное значение 1% прироста А1% =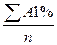 
(29)
На основе базисных темпов роста строится линейный график. На оси абсцисс откладывают периоды времени, а на оси ординат - базисные темпы
роста.
Расчеты показателей рекомендуется представить в табличном виде:
Таблица 2 - Расчет показателей динамики
| Годы
| Уровни ряда | Абсолютный прирост | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста | |||
| цепной | базисный | цепной | базисный | цепной | базисный | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Тема 4 Индексы
Статистические индексы применяются для характеристики сложных социально - экономических совокупностей, состоящих из разнородных, непосредственно несоизмеримых величин.
Индивидуальные индексы — характеризуют изменение только одного элемента совокупности, различают индексы:
цены: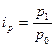 
(3О); количества 
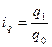(31); товарооборота 
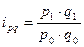(32)
Агрегатные индексы характеризуют изменение нескольких элементов совокупности:
Физического объема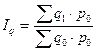 
(33)
Разница между числителем и знаменателем индекса обозначает абсолютное изменение товарооборота за счет изменения физического объема.
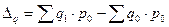(34)
Цены и других качественных показателей
Если за базу сравнения принимаются показатели отчетного периода, используются формулы Пааше:
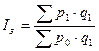(35)
Разница между числителем и знаменателем называют абсолютный прирост товарооборота (выручки, продаж) в результате изменения цен или экономию перерасход денежных средств населения в результате среднего снижения (повышения) цен.
Если за базу сравнения применяются показатели базисного периода используют формулы Ласпейреса
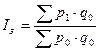(36)
Разница между числителем и знаменателем показывает условный абсолютный прирост товарооборота, если бы объем продаж в отчетном и базисном периоде совпали.
Товарооборота (выручки от реализации или продаж)
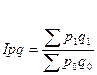(37)
Разница между числителем и знаменателем показывает абсолютное изменение товарооборота за счет совместного индекса обоих факторов.
Формулы средних индексов из индивидуальных:
Физического объема: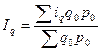 
(38)
Цены: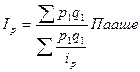 
(39) 
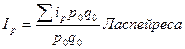(40)
Если индексы качественных показателей построены по формулам Пааше, то между индексами существует следующая связь:
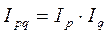(41)
На динамику качественных показателей, уровни которых выражены средними величинами, оказывает влияние изменения структуры изучаемого явления. В этом случае применяется индексный метод с использованием системы взаимосвязанных индексов.
1. Индекс переменного состава представляет собой отношение двух взвешенных средних с изменяющимися (переменными) весами.
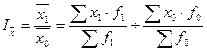(42)
2. Индекс постоянного состава — отношение средних взвешенных с одними и теми же весами (при постоянной структуре)
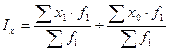(43)
3. Индекс структурных сдвигов — характеризуют изменения.
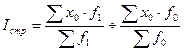(44)
Между этими индексами существует следующая взаимосвязь: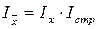 
(45)
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
ВАРИАНТ №1
Задание1. Имеются данные о выпуске продукции по 45 предприятиям (млн. руб.):
| 92 | 101 | 45 | 92 | 98 | 110 | 60 | 46 | 47 | 98 | 107 | 67 | 39 | 44 | 46 |
| 66 | 100 | 104 | 55 | 78 | 47 | 79 | 48 | 54 | 55 | 99 | 56 | 44 | 81 | 48 |
| 99 | 53 | 108 | 48 | 65 | 56 | 100 | 108 | 62 | 75 | 56 | 30 | 50 | 61 | 98 |
Сгруппируйте данные, образовав пять групп с равными интервалами, и определите:
v средний размер выпуска продукции
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v сделайте выводы
Задание 2. В результате опроса методом случайного отбора выяснилось, что 600 человек из 1200 одобрили проводимые мэрией мероприятия. С вероятностью 0,997 определите пределы, в которых находится доля лиц, одобривших мероприятия.
Задание 3.Имеются следующие данные о валовом сборе зерна в одной из областей, млн. т:
| 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| 107 | 103 | 99 | 95 | 89 | 78 | 63 | 69 |
Определите:
v среднегодовое производство валового сбора зерна
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v выявите основную тенденцию валового сбора зерна методом аналитического выравнивания и дайте прогноз валового сбора на 2003год
Задание 4.
Имеются данные о товарообороте магазина и об изменении физического объема товарооборота:
| Товарные группы | Товарооборот, тыс. руб. | Изменение физического объема товарооборота, % | |
| в базисном периоде | в отчетном периоде | ||
| Мука | 1638, 0 | 2517,5 | + 2 |
| Крупа | 187,5 | 270,0 | +20 |
Определите:
v индивидуальный и общий индексы физического объема товарооборота
v общий индекс товарооборота в действующих ценах
v общий индекс цен, используя взаимосвязь индексов
v сумму дополнительных расходов населения при покупке товаров в связи с ростом цен
ВАРИАНТ №2
Задание 1.
Имеются данные о стаже 45 работников одного предприятия (лет):
| 17 | 11 | 12 | 1 | 1 | 12 | 14 | 25 | 3 | 22 | 4 | 17 | 12 | 15 | 16 |
| 15 | 3 | 21 | 10 | 16 | 11 | 8 | 7 | 15 | 20 | 11 | 8 | 4 | 7 | 12 |
| 14 | 2 | 11 | 1 | 23 | 7 | 6 | 4 | 12 | 5 | 6 | 6 | 3 | 10 | 11 |
Осуществите группировку рабочих по стажу, образовав три группы и, охарактеризуйте её следующими показателями:
v средним стажем работы
v дисперсией и средним квадратическим отклонением
v коэффициентом вариации
v модой и медианой
v сделайте выводы
Задание 2.
Для изучения естественной убыли произведено 5% выборочное обследование партии товаров. При этом 10 образцов оказались нестандартными. Определите с вероятностью 0, 997 возможные пределы доли нестандартной продукции.
Задание 3.Имеются следующие данные о конечном потреблении домашних хозяйств в расчете на душу населения в России, руб.
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 6361 | 8888 | 10839 | 12326 | 19617 | 26364 |
Определите:
v среднегодовое значение показателя
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v постройте график динамики базисных темпов исчисленных показателей
Задание 4.
Имеются данные о вкладах населения в Сбербанке:
| Группы населения | Размер вклада, руб. | Удельный вес вкладов в общем числе | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Городское | 500 | 540 | 0,5 | 0,6 |
| Сельское | 420 | 480 | 0,5 | 0,4 |
Определите:
v общие индексы среднего размера вклада для всего населения (переменного, постоянного состава, структурных сдвигов)
v сделайте выводы
ВАРИАНТ №3
Задание 1.
Имеются данные о среднесписочной численности работников 50 предприятий, человек
| 125 | 98 | 456 | 167 | 223 | 213 | 478 | 250 | 134 | 189 |
| 239 | 117 | 360 | 95 | 467 | 98 | 245 | 235 | 213 | 210 |
| 437 | 500 | 111 | 321 | 345 | 458 | 200 | 467 | 321 | 308 |
| 500 | 50 | 134 | 99 | 134 | 367 | 150 | 231 | 235 | 260 |
| 200 | 147 | 256 | 100 | 99 | 106 | 347 | 90 | 478 | 500 |
Осуществите группировку предприятий по среднесписочной численности, образовав пять групп и рассчитайте:
v среднюю численность
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v сделайте выводы
Задание 2.
Какое количество операционистов нужно обследовать в банках региона, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 1 тыс. руб. при среднем квадратическом отклонении заработной платы 5 тыс. руб.
Задание 3.
Имеются данные о динамике численности персонала угольной промышленности России:
| 1998 | 1999 | 2000 | 2001 | 2002 |
| 415 | 370 | 345 | 336 | 295 |
Определите:
v среднегодовое значение показателя
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v выявите основную тенденцию конечного потребления методом аналитического выравнивания и дайте прогноз на 2003год
Задание 4
На основании приведенных данных о реализации продуктов питания рассчитайте:
v агрегатные индексы цен и количества
v агрегатный индекс фактического товарооборота
v сумму дополнительных расходов населения из-за роста цен
|
| Базисный период | Отчетный период | ||
| количество, кг | цена за 1 кг, руб. | количество, кг | цена за 1 кг, руб. | |
| Говядина | 350 | 60 | 470 | 70 |
| Свинина | 400 | 75 | 450 | 80 |
| Баранина | 290 | 55 | 310 | 60 |
ВАРИАНТ №4
Задание 1.
Задание 2.
На предприятии работает 1000 человек. Предполагается провести их выборочное обследование методом случайного бесповторного отбора для определения среднего стажа работы. Сколько человек составит численность выборки при условии, что с вероятностью 0, 954 ошибка выборки не превысит одного человека при среднем квадратическом отклонении 2 человека.
Задание 3.
На основании данных о движении наличной иностранной валюты на территории РФ (млн. долларов США) определите аналитические показатели динамики:
v среднегодовое поступление валюты
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v выявите основную тенденцию поступления наличной иностранной валюты методом аналитического выравнивания и дайте прогноз на 2005год
| Год | 1998 | 1999 | 2000 | 2001 | 2002 |
| Поступление наличной иностранной валюты | 55173,3 | 32563,9 | 36432,5 | 49438,8 | 65369,5 |
Задание 4.
Себестоимость и выпуск продукции на предприятии характеризуются следующими данными:
| Вид продукции | Единица измерения | Себестоимость, руб. | Выпущено продукции в отчетном периоде, тыс. ед. | |
| Базисный период | Отчетный период | |||
| 1 | м2 | 30 | 34 | 4,8 |
| 2 | т | 1500 | 1620 | 0,3 |
| 3 | шт | 42 | 51 | 6,4 |
Определите, на сколько возросли затраты на производство продукции за счет среднего увеличения себестоимости.
ВАРИАНТ №5
Задание 1.
Проведите группировку банков по размеру кредитов (млн. руб.):
| 9,55 | 27,50 | 13,54 | 11,60 | 8,90 | 3,25 | 21,20 | 13,50 | 7,60 | 25,52 |
| 13,38 | 20,15 | 6,10 | 13,36 | 19,62 | 11,90 | 5,20 | 17,90 | 12,30 | 2,50 |
| 22,33 | 5,40 | 12,18 | 17,10 | 1,00 | 12,12 | 16,45 | 26,50 | 23,98 | 13,24 |
Образуйте пять групп банков и определите:
v средний размер кредитов
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v сделайте выводы
Задание 2.
Для определения среднего возраста рабочих предприятия была произведена выборка рабочих методом случайного бесповторного отбора. В результате обследования получены следующие данные:
| Возраст рабочих, лет | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 |
| Число рабочих, чел. | 20 | 60 | 15 | 5 |
С вероятностью 0,997 определите:
а) пределы, в которых находится средний возраст рабочих предприятия;
б) пределы, в которых находится доля рабочих предприятия в возрасте старше 50 лет
Задание 3.
Имеются данные о динамике внешней торговли России (в фактических ценах), % по отношению к предыдущему году:
| Показатель | 1990 | 1991 | 1992 | 1993 | 1994 |
| Экспорт | 88,5 | 71,6 | 78,5 | 101,4 | 108,4 |
| Импорт | 98,1 | 54,4 | 78,7 | 73,0 | 105,4 |
Известно, что в 1990 году объем экспорта составил 71 млрд. долл., в 1994 – 48 млрд. долл.; импорта соответственно 82 и 28 млрд. долл.
Исчислите по экспорту и импорту:
v фактические уровни за исследуемые годы
v базисные темпы
v среднегодовые темпы
v коэффициент опережения экспорта над импортом
Задание 4.
Имеются следующие данные о продажах товаров на одном из рынков:
| Вид товаров | Единица измерения | Продано товаров, тыс. ед. | Цена, руб. | ||
| ноябрь | декабрь | ноябрь | декабрь | ||
| Фрукты | кг | 23 | 25 | 16 | 18 |
| Овощи | кг | 42 | 46 | 9 | 10 |
| Молоко | л | 15 | 13 | 10 | 12 |
Определите:
v Индивидуальные индексы цен по каждому товару
v Общие индексы цен по формулам Ласпейреса и Пааше
v перерасход денежных средств населением в результате повышения цен на товары
ВАРИАНТ 6
Задание 1.
Распределение предприятий региона по размеру прибыли характеризуется следующими данными (млн. руб.):
| 10,1 | 30,0 | 23,7 | 42,9 | 22,7 | 50,0 | 22,9 | 44,0 | 26,5 | 25,0 | 21,1 | 22,7 |
| 30,1 | 20,1 | 12,0 | 23,4 | 21,0 | 13,9 | 32,8 | 38,3 | 40,2 | 25,5 | 32,4 | 27,1 |
| 40,8 | 24,0 | 35,7 | 12,4 | 25,9 | 25,4 | 10,0 | 27,1 | 23,7 | 16,8 | 28,3 | 10,0 |
| 21,6 | 44,8 | 17,6 | 40,0 | 23,9 | 49,8 | 16,4 | 33,3 | 11,0 | 43,0 | 44,5 | 43,8 |
| 39,7 | 22,0 | 10,0 | 34,9 | 45,6 | 37,0 | 23,4 | 19,5 | 17,4 | 24,9 | 19,4 | 10,3 |
Образуйте четыре группы предприятий по размеру прибыли и определите:
v средний размер прибыли
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v сделайте выводы
Задание 2.
С целью прогнозирования урожая пшеницы в хозяйстве была произведена 10 % серийная выборка, в которую попало три участка. В результате обследования установлено, что урожайность пшеницы на участках составила 20, 25 и 21 ц/га.
С вероятностью 0,954 определите пределы, в которых находится средняя урожайность пшеницы в хозяйстве.
Задание 3
Имеются данные о вводе в действие жилых домов предприятиями всех форм собственности за 1996-2002 гг., млн. кв. м. общей площади.
| 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| 16,8 | 28,7 | 30,7 | 32,0 | 30,3 | 31,7 | 33,8 |
Определите:
v среднегодовое значение показателя
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v выявите основную тенденцию ввода в действие жилых домов методом аналитического выравнивания и дайте прогноз на 2005год
v проанализируйте полученные результаты
Задание 4.
Имеются данные по двум отраслям экономики:
| Отрасль | Базисный период | Отчетный период | ||
| Выработка продукции на одного работника, тыс. руб. | Среднесписочная численность работников, чел. | Выработка продукции на одного работника, тыс. руб. | Среднесписочная численность работников, чел. | |
| 1 | 2200 | 600 | 2000 | 500 |
| 2 | 700 | 600 | 800 | 650 |
Определите индексы производительности труда:
v по каждой отрасли экономики
v по двум отраслям вместе индексы постоянного и переменного состава и структурных сдвигов
v сделайте выводы
ВАРИАНТ 7
Задание 1.
По 25 предприятиям отрасли имеются следующие данные о потреблении сырья, тыс. т.:
| 3,2 | 4,1 | 2,2 | 1,6 | 4,4 |
| 10,5 | 2,6 | 5,7 | 9,5 | 5,0 |
| 2,8 | 8,1 | 6,0 | 6,2 | 10,6 |
| 8,3 | 6,1 | 9,8 | 9,6 | 13,3 |
| 12,3 | 7,7 | 13,1 | 19,5 | 21,6 |
Образуйте пять групп предприятий по размеру потребления сырья и определите:
v средний размер потребления сырья
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v постройте гистограмму распределения предприятий
v сделайте выводы
Задание 2.
Для определения среднего срока пользования краткосрочным кредитом в банке была проведена 10%выборка, в которую попало 150 счетов. В результате было установлено, что средний срок пользования краткосрочным кредитом 28 дней при среднем квадратическом отклонении 8 дней. С вероятностью 0,997 определить пределы, в которых будет находиться срок пользования краткосрочным кредитом.
Задание 3.
Имеются следующие данные по РФ за первое полугодие 2003 года об обороте общественного питания млрд. руб.:
| Январь | Февраль | Март | Апрель | Май | Июнь |
| 12,2 | 12,0 | 13,2 | 14,0 | 14,1 | 15,5 |
Определите:
v среднегодовое значение показателя
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v абсолютное значение одного процента прироста и его среднее значение
v постройте график динамики базисных темпов исчисленных показателей
v проанализируйте полученные результаты
Задание 4.
Имеются следующие данные о реализации продукции в первом и втором полугодиях:
| Вид продукции | Единица измерения | Выручка от реализации во 2 полугодии, млн. руб. | Изменение цены во 2 полугодии по отношению к первому |
| А | л | 3,17 | +10 |
| С | кг | 2,4 | без изменения |
Определите:
v на сколько процентов в среднем изменились цены на всю реализованную продукцию во втором полугодии по сравнению с первым
v прирост выручки от реализации за счет среднего изменения цен
ВАРИАНТ 8
Задание 1.
Имеются данные по 25 предприятиям отрасли об объеме электропотребления, кВт·ч:
| 2,3 | 5,7 | 4,2 | 4,6 | 4,6 |
| 4,7 | 4,0 | 3,8 | 2,2 | 3,9 |
| 1,0 | 2,0 | 4,5 | 3,5 | 6,5 |
| 2,0 | 2,1 | 2,3 | 8,5 | 5,3 |
| 2,7 | 1,6 | 5,0 | 4,2 | 7,8 |
Образуйте три группы предприятий по объему электропотребления и определите:
v средний размер показателя
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v постройте гистограмму распределения
v сделайте выводы
Задание 2.
Для выявления затрат времени на обработку деталей рабочими разной квалификации на предприятии была произведена 10%-я типическая выборка (внутри групп произведен механический отбор). Результаты обследования могут быть представлены следующим образом:
| Группы рабочих по разряду | Число рабочих | Средние затраты времени на обработку одной детали, мин. | Среднее квадратическое отклонение, мин. |
| 1 | 30 | 10 | 1 |
| 2 | 50 | 14 | 4 |
| 3 | 20 | 20 | 2 |
С вероятностью 0,954 определите пределы, в которых находятся средние затраты времени на обработку деталей рабочими.
Задание 3.
Имеются данные о динамике экспорта в РФ за период с 1990-2002 г.г., млрд. долларов:
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| 71,1 | 50,9 | 53,6 | 59,6 | 67,4 | 82,4 | 89,7 | 86,9 | 74,4 | 75,6 | 105,0 | 101,9 | 107,2 |
Определите:
v среднегодовое значение показателя
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v выявите основную тенденцию динамики экспорта методом скользящей средней
Задание 4.
Имеются следующие данные о реализации товаров:
| Группы товаров | Товарооборот, тыс. руб. | Изменение цен в отчетном периоде, % | |
| базисный период | отчетный период | ||
| Продовольственные | 34,8 | 36,7 | +7 |
| Непродовольственые | 30,6 | 29,0 | +4 |
Определите:
v средний индекс физического объема товарооборота
v средний индекс цен
v индекс фактического товарооборота
v изменение бюджета населения за счет изменения цен
ВАРИАНТ 9
Задание 1.
Имеются данные о потерях рабочего времени на предприятиях отрасли за год, тыс. человеко –часов:
| 66,0 | 44,0 | 91,0 | 78,0 | 57,4 | 42,0 | 100,0 | 79,8 | 57,0 | 38,0 |
| 23,1 | 112,0 | 72,0 | 55,7 | 36,0 | 85,2 | 72,8 | 54,6 | 37,0 | 56,4 |
| 56,0 | 70,4 | 53,6 | 34,9 | 55,4 | 52,0 | 20,4 | 53,1 | 12,0 | 46,0 |
Образуйте четыре группы предприятий по размеру потерь рабочего времени и определите:
v средний размер потерь
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v сделайте выводы
v постройте гистограмму распределения
Задание 2.
Для установления доли стандартного товара во всей партии игрушек, состоящих из 4000штук, методом случайной бесповторной выборки проверено 40 штук.
В результате установлено, что 30 игрушек соответствуют стандарту. Определите с вероятностью 0,954, в каких пределах находится доля стандартных игрушек во всей партии.
Задание 3.
Имеются данные о производстве овощей в России в 1998-2002 г.г., млн. тонн:
| 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| 11,2 | 10,3 | 20,4 | 10,0 | 9,8 | 9,6 | 11,3 | 10,7 | 11,1 | 10,5 | 12,3 | 12,5 | 13,3 | 12,9 |
Определите:
v среднегодовое значение показателя
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v выявите основную тенденцию производства овощей методом скользящей средней
Задание 4.
Имеются данные о товарообороте одного из районов города, тыс. руб.:
Продукты
Товарооборот
Индивидуальные индексы количества
Определите:
v индекс физического объема товарооборота
v средний индекс цен
v индекс фактического товарооборота
v изменение бюджета населения за счет изменения цен
ВАРИАНТ 10
Задание1.
Имеются данные о стоимости основного капитала на 30 предприятиях отрасли (млн.руб.):
| 54,6 | 73,6 | 42,0 | 46,0 | 62,0 | 68,4 | 36,0 | 49,6 | 62,4 | 71,2 |
| 78,8 | 51,0 | 60,8 | 69,0 | 70,4 | 50,0 | 55,0 | 58,4 | 83,2 | 75,2 |
| 67,2 | 64,2 | 65,0 | 76,2 | 68,0 | 65,6 | 87,2 | 71,8 | 69,2 | 96,0 |
Образуйте три группы предприятий по размеру основного капитала и определите:
v средний размер основного капитала
v дисперсию и среднее квадратическое отклонение
v коэффициент вариации
v моду и медиану
v сделайте выводы
v постройте гистограмму распределения
Задание 2.
При проведении бесповторного выборочного обследования обеспеченности населения стиральными машинами был проведен опрос 125 семей из 2500. При этом выяснилось, что стиральные машины не имеют 25 семей. Определите с вероятностью 0,997 пределы, в которых находится доля семей, не имеющих стиральных машин.
Задание 3.
На основании ниже приведенных данных о производстве мяса (в убойной массе), млн. тонн, в РФ в 1989 – 2002 г.г., определите:
v среднегодовое значение показателя
v цепные и базисные абсолютные приросты, темпы роста и прироста
v средние значения абсолютного прироста, темпа роста и прироста
v проанализируйте полученные результаты
v выявите основную тенденцию производства мяса методом скользящей средней
| 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| 10,1 | 10,1 | 9,4 | 8,3 | 7,5 | 6,8 | 5,8 | 5,3 | 4,9 | 4,7 | 4,3 | 4,4 | 4,5 | 4,5 |
Задание 4.
Фактический товарооборот отчетного года увеличился по сравнению с прошлым на 12%, что составило 280 тыс. руб. Сумма перерасхода денежных средств населения в результате повышения цен составила 128 тыс. руб.
Определите объем фактического товарооборота в отчетном и базисном периодах, индекс фактического товарооборота, средние индексы цен и физического объема товарооборота.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ И ПОДГОТОВКИ К ЗАЧЕТУ
1. Предмет статистики
2. Методы статистики
3. Организация статистики в РФ
4. Понятие и план статистического наблюдения
5. Понятие и классификация статистической отчетности
6. Специально- организованное статистическое наблюдение
7. Виды статистических наблюдений
8. Понятие и виды группировки
9. Методика выполнения группировки
10. Характеристика группировочных признаков
11. Статистические ряды распределения
12. Статистические таблицы: элементы и виды
13. Статистические графики
14. Абсолютные величины
15. Относительные величины
16. Понятие, условия использования средних величин
17. Средняя арифметическая величина: свойства и способы расчета
18. Средняя гармоническая величина
19. Расчет средней геометрической величины
20. Средняя квадратическая и средняя кубическая величины
21. Понятие и расчет моды
22. Понятие и расчет медианы
23. Показатели вариации
24. Понятие, элементы и виды рядов динамики
25. Абсолютные показатели рядов динамики
26. Относительные показатели рядов динамики
27. Средние показатели рядов динамики
28. Понятие об индексах, виды индексов
29. Обозначение индексируемых величин
30. Агрегатный индекс физического объема
31. Агрегатный индекс товарооборота
32. Агрегатный индекс цены Пааше и Ласпейреса
33. Определение агрегатных индексов физического объема и цены через индивидуальные индексы)
34. Взаимосвязь между индексами (мультипликативная и аддитивная модели)
35. Индексы постоянного, переменного состава и индексы структурных сдвигов
36. Статистические методы изучения взаимосвязей
37. Характеристика генеральной и выборочной совокупности
38. Повторная и бесповторная случайная и механическая выборка
39. Типическая выборка
40. Серийная выборка
ЛИТЕРАТУРА
1.Гусаров В.М. Теория статистики: Учебн. пособие для вузов.- М.: Аудит, ЮНИТИ, 2001.-247с.
2.Елисеева И.И. Общая теория статистики: Учебник- М.: Финансы и статистика, 2001.-29с.
3.Ефимова М.Р., Петрова Е.В., Румянцев В.Н.Общая теория статистики: Учебник. – М.: ИНФРА-М, 2001.-416с.
4.Ефимова М.Р. Практикум по общей теории статистики: Учеб.пособие- М.: Финансы и статистика, 2002.- 18с
5. Общая теория статистики: Учебник /под ред. Башиной О.Э., СпиринойА.А., М: Финансы и статистика, 1999
6.Практикум по статистике: Учебн. пособие для вузов/под ред. В.М.Симчеры /ВЗФЭИ.- М.:ЗАО «Финстатинформ», 1999.-259с.
7.Сборник задач по теории статистики: Учебн. пособие/под ред. В.В.Глинского, Л.К. Серга. – М.:ИНФРА – М; Новосибирск, 2002-257с.
8.Статистика: Учебн. пособие для вузов/под ред. Мхитаряна В.С. – М.:Академия, 2003
9.Теория статистики: Учебник/под ред. Г.Л. Громыко – М.:ИНФРА – М,2000.- 414с.
10.Теория статистики: Учебник/ под ред. Р.А. Шмойловой.- М.: Финансы и статистика, 2003. –35с.
КРАТКИЙ КУРС ЛЕКЦИЙ
Таблица 2 - Цена и сумма реализации на товары по трем городам
| Город | Цена, тыс.руб. (х) | Сумма реализации тыс./руб. (w) | Количество реализованных ед. кг. (f) |
| А | 30 | 600 | 20 |
| В | 20 | 1000 | 50 |
| С | 25 | 350 | 14 |
| Итого: | 75 | 1950 | 84 |
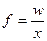
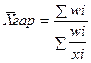
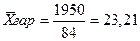тыс. руб.
- Средняя геометрическая - применяется при расчетах средних относительных величин динамики (цепных), т.е. характеризует средний коэффициент роста.
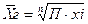- простая 
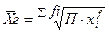- взвешенная
Пример: Темп роста товарооборота по годам составил:
1997г. – 1,053 1999г. – 1,049 1998г. – 1,051 2000г. – 1,058
Определить средний темп роста товарооборота
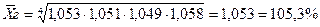
Так же средняя геометрическая может применяться для определения равноудаленной величины от максимального и минимального значения признака.
Пример: Страховая сумма выплат по страховке может изменится от 100 000 до 10 000 руб. в год. Определить среднюю сумму выплат.
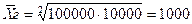руб.
Ответ: Средняя сумма выплат (страховых) в год составляет 1000 рублей.
- Средняя квадратическая – используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической.
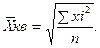- простая 
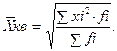- взвешенная
- Средняя кубическая
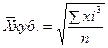- простая 
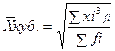- взвешенная
2
Структурные средние величины применяются для изучения внутреннего строения и структуры рядов распределения значений признака.
К ним относится:
Мода – наиболее часто встречающиеся значение признака, т.е. имеющее наибольшую частоту. В интервальном ряду с равными интервалами, мода вычисляется по формуле.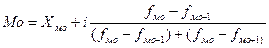 
,
Где xмо – начало модального интервала, нижняя граница
i – величина модального интервала
fмо – частота в модальном интервале
fмо-1 – частота предмодального интервала
fмо+1 –частота послемодального интервала
Медиана – это вариант, который находится в середины вариационного ряда и делит его на две равные части. Для определения медианы вариационного ряда, необходимо его проранжировать и найти порядковый номер медианы.
Медиана, в интервальных рядах, рассчитывается по формуле
,
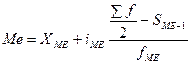Где Xме – начало медианного интервала
Sме-1 – сумма накопленных частот ряда, предшествующего медианному интервалу.
Медианным считается тот интервал, в котором накопленная частота превышает половину суммы всех частот.
3.
Показатели вариации характеризуют колеблемость отдельных значений признака . К ним относится:
Абсолютные показатели
1.1 Размах вариации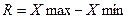 
1.2 Среднее линейное отклонение
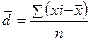для не сгруппированных
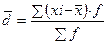для сгруппированных
1.3 Дисперсия – средняя из квадратов отклонений вариантов значений признака от их средней величины
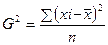для не сгруппированных
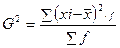для сгруппированных
1.4 Среднее квадратическое отклонение
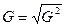
Дисперсия обладает некоторыми свойствами:
- Дисперсия постоянной величины равна нулю
- Если все варианты значений признака уменьшить на одно и то же число, то дисперсия не изменяется.
- Если все варианты значения признака уменьшится в К раз, то дисперсия уменьшится К2 раз.
Относительные показатели вариации
2.1 Относительный размах вариации
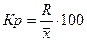
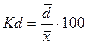
2.2 Коэффициент вариации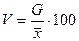 
Если коэффициент вариации более 33%, то вариация является неоднородной.
При сравнении квартальных и месячных данных многих социально-экономических явлений часто обнаруживаются периодические колебания, возникающие под влиянием смены времён года. В статистике они носят название сезонные колебания или сезонные волны.
Существует несколько методов изучений и измерений сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности. Процентные отношения, фактических внутригрупповых уровней к теоретическим расчётным уровням выступающим в качестве базы сравнения. Для расчёта индекса сезонности необходимо иметь помесячные данные, как минимум за три года. Для каждого месяца рассчитывается средний уровень и исчисляется среднемесячный уровень для всего анализируемого ряда
Индексы в статистике
1. Понятия и классификация индексов
2. Способы исчисления индексов
3. Взаимосвязь индексов
1
Относительная величина получаемая в результате сопоставления уровней сложных социально-экономических показателей во времени, в пространстве или по сравнению с планом называется индексом.
Основным элементом индексного отношения является индексируемая величина – значение признака статистической совокупности изменение которой является объектом изучения.
Индексы классифицируют по трём признакам:
1. По характеру изучаемых объектов:
- Индексы количественных показателей: физического объёма продукции и розничного товарооборота, при этом количество оцениваются в сопоставимых ценах.
- Индексы качественных показателей: индексы цены, себестоимости, производительности труда, урожайности и т.д.
- Их расчёт производится на базе неизменных количеств продукции.
2. По степени охвата единиц совокупности:
- Индивидуальные индексы – характеризуют изменения отдельных элементов сложного явления (i).
- Общие индексы – отражают изменения всех элементов сложного явления (I).
3. По методам расчёта общих индексов:
- расчёт агрегатных индексов.
- расчёт средних индексов из индивидуальных.
2
Индексный метод использует следующие обозначения:
1)
Все индексы используют при расчёте уровни базисного периода (0) и уровень отчётного периода (1).
Индивидуальные индексы представляют собой отношение двух индексируемых величин.
Агрегатные (общие) индексы могут быть построены более сложным способом. В этих индексах представляется сумма произведений двух величин, одна из которых меняется (индексируется), а другая остаётся неизменной и в числителе, и в знаменателе (вес индекса).
Формулы агрегатных индексов.
1) Физического объёма
В случае индексов объёмных показателей весами являются качественные показатели (цена) зафиксированные на уровне базисного периода.
Разница между числителем и знаменателем индекса означает абсолютное изменение прироста или снижения товарооборота за счёт изменения физического объёма.
2) Индекс цены и других качественных показателей:
- индекс цены Пааше – сравнение цен с отчётными весами.
- Агрегатный индекс цен с базисными весами (фор-ла Ласпейроса)
Тема 8
План:
- Общие понятия о статистических связях
- Методы выявления наличия корреляционной связи
- Уравнения регрессии
1
Между различными статистическими показателями существует определенная связь. Она выявляется с помощью методов статистики и математики.
Существуют различные типы связей между явлениями:
1. По характеру зависимости:
- Функциональные связи – характеризуются полным соответствием между изменением факторного признака и изменением результативной величины. При этом каждому значению признака фактора соответствует вполне определенное значение результативного признака. У=f(x)
- Корреляционные связи – изменение результативного признака обусловлено влиянием факторного, не всецело, а лишь частично, т.к. возможно влияние прочих факторов. У=f(x)+Е
2.По направлению:
- Прямая связь, при которой с ростом значений факторного признака растут значения результативного признака
- Обратная связь, при которой с увеличение значений одного признака, величина другого уменьшается
3. По аналитическому выражению:
- Линейные - выражаются аналитическим уравнением прямой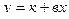 
Криволинейные - выражаются уравнением гиперболы, параболы, показательной, степенной, логарифмической функцией и др.
гиперболическая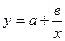 
показательная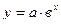 
параболическая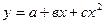 
степенная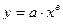 
логарифмическая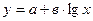 
Параметр в называется коэффициентом регрессии и показывает на сколько в среднем меняется величина результативного признака У при изменении факторного признака (Х) на единицу..
При наличии прямой зависимости В > 1, а обратной В < 1.
2.
Для определения наличия корреляционной связи применяется ряд специфических методов:
1. Метод парной корреляции, т.е. сопоставление 2-х параллельных рядов: ряда значений факторного признака (х) и соответствующего ему значения результативного признака (у).Для установления данной зависимости необходимо ранжировать ряд значений факторного признака.
Если возрастание величины факторного (x) признака влечет за собой возрастание величины результативного (у) говорят, о возможном наличии прямой корреляционной связи, если к уменьшению, то об обратной корреляционной связи.
2.Метод построения групповой или корреляционной таблиц, применяется в случае наличия большого числа различных значений результативного признака, соответствующих одному и тому же значению факторного признака
3. Графический метод – используется для предварительного выявления наличия связи и выбора формы связи. Если линия приближается к прямой, то можно предположить наличие корреляционной связи.
Рассмотрим установление наличия корреляционной связи перечисленными методами на условном примере.
По 20 туристическим фирмам были установлены затраты на рекламу (факторный признак, Х) и количество туристов, воспользовавшихся услугами каждой фирмы (результативный признак У)
| №фирмы | Затраты на рекламу,у.е. | Количество туристов | Знаки отклонений | Совпадения (А) Несовпадения (Б) | |
| х | у | ||||
| 1 | 8 | 800 | - | - | А |
| 2 | 8 | 850 | - | - | А |
| 3 | 8 | 720 | - | - | А |
| 4 | 9 | 850 | - | - | А |
| 5 | 9 | 800 | - | - | А |
| 6 | 9 | 880 | - | - | А |
| 7 | 9 | 950 | - | - | А |
| 8 | 9 | 820 | - | - | А |
| 9 | 10 | 900 | + | - | Б |
| 10 | 10 | 1000 | + | + | А |
| 11 | 10 | 920 | + | - | Б |
| 12 | 10 | 1060 | + | + | А |
| 13 | 10 | 950 | + | - | Б |
| 14 | 11 | 900 | + | - | Б |
| 15 | 11 | 1200 | + | + | А |
| 16 | 11 | 1150 | + | + | А |
| 17 | 11 | 1000 | + | + | А |
| 18 | 12 | 1200 | + | + | А |
| 19 | 12 | 1100 | + | + | А |
| 20 | 12 | 1000 | + | + | А |
По представленному в порядке возрастания факторному признаку и соответствующему ему результативному признаку можно предположить наличие прямой корреляционной связи. Однако, в некоторых вариантах есть и обратное соотношение (фирма 11).Это говорит о том, что на величину результативного признака влияют прочие факторы.
Построение корреляционной таблицы начинают с группировки факторного и результативного признаков. Для факторного признака число групп составит пять. Для результативного признака определим величину интервала по формуле Стэрджесса: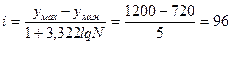 
чел.
В корреляционной таблице факторный признак располагают в строках, а результативный - в столбцах таблицы.
| Середина интервала,у | 768 | 864 | 960 | 1056 | 1152 | fх |
|
| Группы по х и у | 720-816 | 816-912 | 912-1008 | 1008-1104 | 1104-1200 | ||
| 8 | 2 | 1 | 3 | 800 | |||
| 9 | 1 | 3 | 1 | 5 | 864 | ||
| 10 | 1 | 3 | 1 | 5 | 960 | ||
| 11 | 1 | 1 | 2 | 4 | 1032 | ||
| 12 | 1 | 1 | 1 | 3 | 1056 | ||
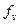
| 3 | 6 | 6 | 2 | 3 | 20 |
Если частоты расположены на диагонали из левого верхнего угла в правый нижний угол, то можно предположить наличие прямой корреляционной зависимости, если справа налево, то об обратной. Для более точного установления наличия связи необходимо рассчитать средние значения результативного признака.
Среднее число туристов для каждой группы определяется по формуле средней арифметической взвешенной:
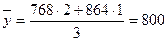чел и т. д.
По средним значениям результативного признака свидетельствует о возможном наличии прямой корреляционной зависимости числа туристов от затрат на рекламу.
Построение групповой таблицы.
Все единицы совокупности разбиваются на группы в зависимости от величины признака – фактора и по каждой группе вычисляются средние значения результативного признака.
| Группы туристических фирм по затратам на рекламу, у.е. | Число фирм в группе | Среднее число туристов, воспользовавшихся услугами фирм, человек |
| 8 | 3 | 790 |
| 9 | 5 | 860 |
| 10 | 5 | 966 |
| 11 | 4 | 1063 |
| 12 | 3 | 1100 |
| Итого | 20 |
Увеличение среднего числа туристов свидетельствует о наличии прямой корреляционной связи.
Также для предварительного выявления наличия связи и определения её характера применяют графический метод.
Полученный график называется полем корреляции, на котором также строится эмпирическая линия связи по средним значениям показателя.
3
Охарактеризовать зависимость результативного признака от факторного можно с помощью показателей тесноты связей:
– коэффициент корреляции знаков
– линейный коэффициент корреляции
– коэффициент детерминации
Наиболее простым показателем тесноты связи является коэффициент корреляции знаков (Фехнера)
Для этого необходимо рассчитать среднее значение х (9,95) и у (952) и сравнить каждое значение признака со средним. Посчитав число совпадений и несовпадений знаков, определяется коэффициент Фехнера, который может принимать значения от -1 до +1. Чем ближе к -1, тем ярче выражена обратная связь, чем ближе к +1 - обратная.
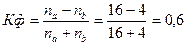
Полученный коэффициент свидетельствует о наличие прямой корреляционной связи.
Более совершенным показателем является линейный коэффициент корреляции.
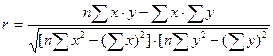
Данный коэффициент также может принимать значения от -1до +1. Чем ближе значение к единице, тем теснее связь между признаками.
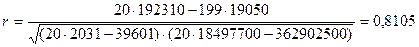
Квадрат коэффициента корреляции носит название коэффициента детерминации. Для рассматриваемого примера его величина составляет 65,69 %, т.е. 65,69% числа клиентов, воспользовавшихся услугами фирмы, объясняется затратами на рекламу своих услуг.
Коэффициент эластичности – показывает, на сколько % изменяется величина результативного признака при изменении факторного признака на 1%
Методы статистики
Статистика базируется на положениях социально-экономической теории и использует:
1. Общенаучные методы, т.е. такие методы, которые применяются и во многих других науках:
¨ диалектические методы познания – изучение явлений в их взаимосвязи;
¨ переход количества в качество;
¨ анализ и синтез;
¨ логика, аналогия и гипотеза;
2.Специфические методы - используются только этой наукой:
2.1 Метод массовых наблюдений – сбор первичной статистической информации.
В его основе лежит закон больших чисел: «В сводных статистических характеристиках действия элементов случайности взаимопогашаются, хотя они и могут проявляться в признаках индивидуальных единиц статистической совокупности»
2.2 Метод статистических группировок, представляющий собой разделение всей массы случаев на однородные группы и подгруппы, подсчет итогов по каждой группе и оформление результатов, т.е. переход от единичных показателей к сводным.
2.3 Обработка и анализ статистической информации – выводы излагаются в текстовой форме и сопровождаются графиками, таблицами, диаграммами.
2.
К основным категориям статистики относятся:
Статистическая совокупность - множество изучаемых явлений объединенных в соответствие с задачей исследования единой качественной стороной.
Явление и процессы можно охарактеризовать с помощью статистических показателей.
Статистический показатель – количественная оценка свойств, изучаемого времени.
Статистические показатели можно разделить на две группы:
1. Учетно-оценочные - изучают объем или уровень явлений на определенный момент времени;
3. Аналитические - используются для характеристики и анализа особенностей развития явления, распространенности в пространстве, динамики, соотношение его отдельных частей.
3.
Изучением экономического и социального развития страны занимаются специально созданные для этого органы, совокупность которых называются статистической службой.
В настоящее время главным учетно-статистическим центром является государственный комитет РФ по статистики и называется ГОСКОМСТАТ РФ. Ему подчиняются республиканские, в краях, в областях, Москве и Санкт-Петербурге – государственные комитеты; в городах – управления государственной статистики.
Наряду с государственной, существует ведомственная статистика, ведущаяся на предприятиях, в организациях, ведомствах и министерствах. Она выполняет работы, связанные с получением, обработкой и анализом статистической информации, необходимой для руководства и планирования их деятельности.
Задачи Госкомстата
6. Сбор, обработка и анализ научно-обоснованных данных, характеризующих экономическое и социальное развитие страны, эффективность производства.
7. Выявление соотношения отраслей экономики, соотношение между размерами производства и потреблением продукции, между экспортом и импортом.
8. Разработка научно-обоснованной статистической методологии, разработка новых форм отчетности.
9. Координация статистической деятельности федеральных и региональных органов исполнительной власти.
10. Представление официальной статистической информации Презеденту, Правительству, Федеральному собранию, общественным и международным организациям (ООН, МВФ, ОЕСД).
3
В связи с переходом на принятую в международной практике систему учета и статистики, в России функционирует Единый государственный регистр предприятий, организаций и объединений (ЕГРПО).
Цель его создания обеспечение единого государственного учета, формирование информационного фонда, который состоит из четырех разделов:
5. Идентификационный – присвоение регистрационного кода объекту;
6. Классификационный – сведения об отраслевой, территориальной принадлежности субъекта, его подчиненности в виде собственности, организационной форме;
7. Справочный – содержит фамилию руководителя, адрес объекта, телефон и пр.
8. Экономический – содержит показатели, характеризующий субъект: средняя численность, стоимость основных средств, балансовая прибыль, уставный фонд, объем выпускаемой продукции.
Держателем ЕГРПО является ГОСКОМСТАТ.
Все явления и процессы характеризуют с помощью статистических показателей дающие количественную оценку явлениям. Множество изучаемых явлений объединенных в соответствие с задачей исследования называется статистической совокупностью.
Статистические показатели могу быть:
1. Учётно-оценочными – характеризуют объём или уровень явления.
2. Аналитические – характеризуют развитие явления, динамику и соотношение его частей.
Методы статистики:
1. Общенаучные:
Теоретические положения социально-экономической теории, диалектические методы познания, гипотеза, аналогия.
2. Специфические:
Находят своё выражение в трёх этапах статистического исследования.
2.1. Метод массовых наблюдений – сбор первичной информации. В основе этого метода лежит закон больших чисел:
В сводных статистических характеристиках действие элементов случайностей взаимопогашаются, хотя они и могут проявляться в признаках индивидуальных единиц совокупности.
2.2. Метод статистических группировок:
Разделение всей массы случаев на однородные группы и подгруппы и оформление результатов, т.е. переход от единичных показателей к сводным.
2.3. Обработка и анализ статистической информации (представление в текстовой форме выводов, сопровождающихся таблицами и графиками.
3
Задачи ГОСКОМСТАТА РФ
1) Сбор, обработка и анализ научно-обоснованных данных, характеризующих социально-экономическое развитие страны.
2) Выявление отраслевых пропорций между производством и потреблением, между экспортом и импортом.
3) Разработка методологии, новых форм отчётности.
4)Представление официальной информации президенту, правительству, федеральному собранию, общественным и международным организациям.
В статистике существует система учёта в виде единого государственного регистра предприятий, организаций и объединений (ЕГРПО). Созданы с целью формирования информационного фонда.
Информационный фонд состоит из:
1. Индетификационный фонд (присвоить определённый фонд).
2. Классификационный (содержит сведения о принадлежности субъекта)
3. Справочный (название, адрес, телефон, ФИО руководителя).
4. Экономический – содержит экономические показатели характеризующие субъект.
Объём выпускаемой продукции, численность, балансовая прибыль.
Также существует информационно-вычислительная сеть в статистике для эффективной обработки и передачи информации. В целях кодирования используют различные цифровые и буквенные коды. Существуют различные общероссийские классификаторы. ОКПД – общероссийский классификатор продукции и видов деятельности. ОКУН – ОК услуг населения.
Статистическое наблюдение
4. Понятия и требования к статистическим наблюдениям.
5. Программа СН.
6. Формы и виды СН.
1
СН – планомерный, научно-обоснованный сбор данных о социально-экономических явлениях и процессах.
СН проводится в три этапа статистических методов.
Требования к статистическим данным:
1. Достоверность данных
2.Сопоставимость данных
3.Своевременость
СН может проводиться органами государственной статистики и различными независимыми институтами и организациями.
2
СН проводится в соответствии с программой состоящей из двух частей: 1. « Програмнометодологическая» - содержит цель, устанавливает объект наблюдения – совокупность явлений и процессов, охватываемых наблюдением.
Единица наблюдения – элемент совокупности являющийся носителем регистрируемых признаков.
2.«Организационная» - содержит информацию об органах наблюдения, порядке приёма и сдачи информации, предоставлении предварительных и окончательных итогов.
Сезон наблюдения – время года, когда изучаемый объект находится в привычном для него состоянии.
Период наблюдения – время на которое регистрируются данные.
Статистический инструментарий: бланки документов (анкеты, формы отчётности, переписные листы), инструкции.
3
Существует две формы СН:
Статистическая отчётность – официальный документ содержащий сведения о работе подотчетного объекта, занесённые на специальную форму.
Государственная статистическая отчётность утверждается Госкомстатом, основывается на первичном учёте и является его обобщением.
Первичный учёт – регистрация фактов, производимая по мере их совершения на первичном учётном документе.
Существует «Положение о порядке представления государственной статистической отчётности», в котором предусмотрены административные взыскания за несоблюдения сроков, искажения информации и непредставление данных.
Основные реквизиты отчётности:
Статистические показатели.
Абсолютные и относительные величины статистики.
3. Абсолютные величины и их виды.
4. Относительные величины и их виды.
1
Показатели, с помощью которых статистика характеризует совокупности единиц в целом и по группам называется обобщающими показателями. К ним относят абсолютные, относительные и средние величины.
Первоначальным видом обобщающим показателей являются абсолютные величины. Их получают в результате статистического наблюдения. Сводки или суммирования первичного статистического материала или расчётным путём, таким образом, абсолютные величины характеризуют численность совокупности и объём изучаемого явления. Все абсолютные величины являются, именованы числами, т.е. имеют единицы измерения.
Виды единиц измерения:
4. Натуральные – применяются тогда, когда единицы измерения соответствуют потребительским свойствам продукта. Единица измерения могут быть простыми и сложными.
5. Стоимостные – получаются умножения количества единиц на цену единицы.
6. Условно-натуральные – применяются, если разновидности продукции обладают общностью одного потребительского свойства.
Абсолютные величины могут быть индивидуальными и суммарными.
2
Относительные величины – характеризуют количественное соотношение сравниваемых абсолютных величин и представляют собой частное от деления двух статистических величин:
В числителе всегда находится сравниваемая величина (то, что сравнивают), а в знаменателе база сравнения, то с чем сравнивают.
Форма выражения относительных величин:
5. Коэффициенты (доли). База сравнения принимается за единицу.
6. Проценты. База сравнения принимается за сто.
7. Промилле. База сравнения принимается за тысячу (%0).
8. Продецимилле. База сравнения принимается за 10.000 (%00).
Виды относительных величин:
8. Относительные показатели планового задания - отношение уровня запланированного на предстоящий период к уровню показателя достигнутого в предыдущем периоде.
9. Относительный показатель выполнения плана – отношение фактически достигнутого уровня в текущем периоде к уровню планируемого показателя на этот же период.
10. Относительные показатели динамики характеризуют изменения уровня развития какого-либо явления во времени.
11. Относительные показатели структуры характеризуют состав изучаемой совокупности, доли или удельные веса элементов совокупности в общем итоге и представляют собой отношение части единиц совокупности ко всему объёму совокупности.
12. Относительные показатели интенсивности – характеризуют степь развития данного явления в определённой среде и могут выражаться в кратных отношениях, в процентах и промилле.
13. Относительные показатели координации характеризуются отношением частей совокупности к одной из них принятой за базу сравнения, она показывает во сколько раз одна часть совокупности больше другой, или сколько единиц одной части совокупности приходится на одну, десять, сто или тысячу единиц другой части.
14. Относительные показатели сравнения – характеризуют отношение одноимённых абсолютных показателей, соответствующих одному и тому же периоду или моменту времени, но к различным объектам или территориям.
Средние величины в статистике
4. Понятие и виды степенных средних величин.
5. Структурные средние величины.
6. Показатели вариации.
1
Средняя величина – обобщающая характеристика изучаемого признака, отражающая его типичный уровень в расчёте на единицу совокупности в конкретных условиях места и времени.
Средние величины – это общая характеристика совокупности по количественному признаку, показывающему уровень признака, которая относится ко всей совокупности.
Основным условием научного использования средней величины является качественная однородность совокупности. Средние величины являются именованными числами и имеют ту же размерность, что и признак у отдельных единиц совокупности.
Средние величины могут быть:
· общими – рассчитанные по совокупности в целом
· групповыми – исчисленные для каждой группы
Виды средних величин
1. Степенные средние величины
В основе их расчета лежит общая формула: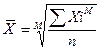 
,
если m = 1 – средняя арифметическая
m = -1 – средняя геометрическая
m = 0 – средняя геометрическая
m = 2 – средняя квадратическая
m = 3 – средняя кубическая
У степенных средних есть свойство возрастать с повышением степеней (показателя), которое называется правилом мажорантности средних.
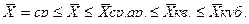
Степенные средние величины могут быть простыми и взвешенными.
2.Структурные средние величины: мода и медиана
1.1 Средняя арифметическая – применяется в тех случаях, когда объем варьирующего признака для всей совокупности является сумма значений признаков отдельных ее единиц.
Средняя арифметическая простая
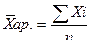
Средняя арифметическая взвешенная
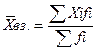
Пример: Вычислить средний стаж 10 работников по данным: 6.5.4.3.3. 4.5.4.5.4.
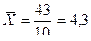лет (простая); 
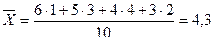лет(взвешенная)
Средняя арифметическая обладает некоторыми свойствами:
1) Если значение признака каждой единицы совокупности уменьшить или увеличить на одну и ту же величину А, то со средней произойдут те же изменения.
2) Если значение признака каждой единицы умножить или разделить на постоянное число А, то средняя арифметическая уменьшится или увеличится в А раз.
3) Если частоту каждого значения признака уменьшить или увеличить в n раз, средняя арифметическая не изменится.
Эти свойства используются для упрощения расчетов средней « способом моментов»
Для этого выбирается значение признака обладающего наибольшей частотой.
Пример: Рассчитаем среднюю арифметическую «способом моментов» по следующим данным:
Таблица 1 - Распределение предприятий по стоимости ОПФ:
| Группы предприятий по стоимости ОПФ млн. руб. | Число предприятий f | Серединный интервал, x |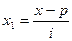 
| 
|
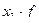
| 14-16 | 2 | 15 | -2 | -4 |
| 16-18 | 6 | 17 | -1 | -6 |
| 18-20 | 10 | 19 | 0 | 0 |
| 20-22 | 4 | 21 | 1 | 4 |
| 22-24 | 3 | 23 | 2 | 6 |
| Итого: | 25 | – | 0 | 0 |
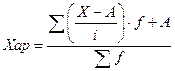
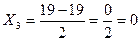
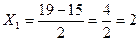
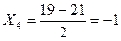
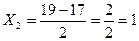
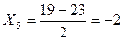
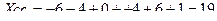
1.2 Средняя гармоническая – величина обратная средней арифметической, применяется, когда статистическая информация не содержит частоты по отдельным вариантам совокупности, а представлена, как их произведение, или при расчете общей средней из среднегрупповых.
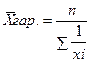- простая
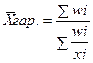- взвешенная
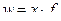- вес средней
Пример: Определить среднюю цену на товар по следующим данным.
Таблица 2 - Цена и сумма реализации на товары по трем городам
| Город | Цена, тыс.руб. (х) | Сумма реализации тыс./руб. (w) | Количество реализованных ед. кг. (f) |
| А | 30 | 600 | 20 |
| В | 20 | 1000 | 50 |
| С | 25 | 350 | 14 |
| Итого: | 75 | 1950 | 84 |
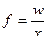
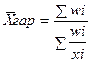
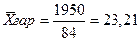тыс. руб.
1.3 Средняя геометрическая - применяется при расчетах средних относительных величин динамики (цепных), т.е. характеризует средний коэффициент роста.
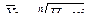- простая 
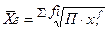- взвешенная
Пример: Темп роста товарооборота по годам составил:
1997г. – 1,053 1999г. – 1,049
1998г. – 1,051 2000г. – 1,058
Определить средний темп роста.
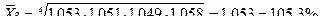
Ответ: средний темп роста т/о составил по годам (1987 – 1990г.) – 105,3%, а средний прирост составил 5,3%
Так же средняя геометрическая может применяться для определения равноудаленной величины от максимального и минимального значения признака.
Пример: Страховая сумма выплат по страховке может изменится от 100 000 до 10 000 руб. в год. Определить среднюю сумму выплат.
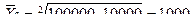руб.
Ответ: Средняя сумма выплат (страховых) в год составляет 1000 рублей.
1.4 Средняя квадратическая – используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической.
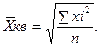- простая 
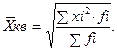- взвешенная
1.5. Средняя кубическая
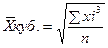- простая 
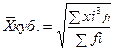- взвешенная
Применение этих величин ограничено: если средний размер признака представлен в квадратных или кубических единицах измерения.
2.
Структурные средние величины применяются для изучения внутреннего строения и структуры рядов распределения значений признака.
К ним относится:
2.1Мода – наиболее часто встречающиеся значение признака, т.е. имеющее наибольшую частоту. В интервальном ряду с равными интервалами, мода вычисляется по формуле.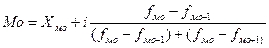 
xмо – начало модального интервала, нижняя граница
i – величина модального интервала
fмо – частота в модальном интервале
fмо-1 – частота предмодального интервала
fмо+1 –частота послемодального интервала
2.2.Медиана – это вариант, который находится в середины вариационного ряда и делит его на две равные части. Для определения медианы вариационного ряда, необходимо его проранжировать и найти порядковый номер медианы.
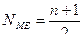NМЕ – порядковый номер медианы
Рассмотрим пример со стажем (лет)
3, 3, 4, 4, 4, 4, 5, 5, 5, 6.
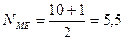
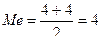
Ответ: Половина работников имеет стаж менее 4 лет, а половина более 4 лет.
Медиана, в интервальных рядах, рассчитывается по формуле
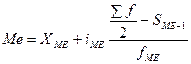
Xме – начало медианного интервала
Sме-1 – сумма накопленных частот ряда, предшествующих медианному интервалу.
Медианным считается тот интервал, в котором накопленная частота превышает половину суммы всех частот.
3.
Показатели вариации характеризуют колеблемость отдельных значений признака. К ним относится:
1. Абсолютные показатели
1.1 размах вариации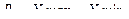 
1.2 Среднее линейное отклонение
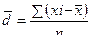для не сгруппированных
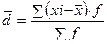для сгруппированных
1.3 Дисперсия – средняя из квадратов отклонений вариантов значений признака от их средней величины
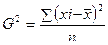для не сгруппированных
для сгруппированных
1.3 Среднее квадратическое отклонение
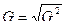
Дисперсия обладает некоторыми свойствами:
1 Дисперсия постоянной величины равна нулю
2 Если все варианты значений признака уменьшить на одно и то же число, то дисперсия не изменяется.
3 Если все варианты значения признака уменьшится в К раз, то дисперсия уменьшится К2 раз.
2. Относительные показатели вариации
2.1 Относительный размах вариации
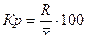
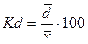
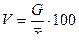V – коэффициент вариации
Виды и методы анализа рядов динамики
4. Понятия и виды рядов динамики.
5. Показатели рядов динамики.
6. Средние показатели рядов динамики.
1
Ряд динамики (временной) – ряд расположенный в хронологической последовательности статистических показателей.
Каждый ряд динамики состоит из двух элементов:
1) период времени к которому относятся статистические показатели.
2) Статистические показатели характеризующие изучающий объект (уровень ряда).
Статистические показатели могут быть представлены абсолютными, относительными и средними величинами.
Существует два способа сопоставления уровней ряда
3. Если каждый уровень сравнивается с одним и тем же предшествующим, то это сравнение с постоянной базой и получаемые показатели называются базисными.
4. Если каждый уровень ряда сравнивается с непосредственно ему предшествующим, т.е. с переменной базой, то получаемые показатели называются цепными.
2
При сравнении квартальных и месячных данных многих социально-экономических явлений часто обнаруживаются периодические колебания, возникающие под влиянием смены времён года. В статистике они носят название сезонные колебания или сезонные волны.
Существует несколько методов изучений и измерений сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности. Процентные отношения, фактических внутригрупповых уровней к теоретическим расчётным уровням выступающим в качестве базы сравнения. Для расчёта индекса сезонности необходимо иметь помесячные данные, как минимум за три года. Для каждого месяца рассчитывается средний уровень и исчисляется среднемесячный уровень для всего анализируемого ряда
Индексы в статистике
4. Понятия и классификация индексов
5. Способы исчисления индексов
6. Взаимосвязь индексов
1
Относительная величина получаемая в результате сопоставления уровней сложных социально-экономических показателей во времени, в пространстве или по сравнению с планом называется индексом.
Основным элементом индексного отношения является индексируемая величина – значение признака статистической совокупности изменение которой является объектом изучения.
Индексы классифицируют по трём признакам:
4. По характеру изучаемых объектов:
- Индексы количественных показателей: физического объёма продукции и розничного товарооборота, при этом количество оцениваются в сопоставимых ценах.
- Индексы качественных показателей: индексы цены, себестоимости, производительности труда, урожайности и т.д.
- Их расчёт производится на базе неизменных количеств продукции.
5. По степени охвата единиц совокупности:
- Индивидуальные индексы – характеризуют изменения отдельных элементов сложного явления (i).
- Общие индексы – отражают изменения всех элементов сложного явления (I).
6. По методам расчёта общих индексов:
- расчёт агрегатных индексов.
- расчёт средних индексов из индивидуальных.
2
Индексный метод использует следующие обозначения:
1)
Все индексы используют при расчёте уровни базисного периода (0) и уровень отчётного периода (1).
Индивидуальные индексы представляют собой отношение двух индексируемых величин.
Агрегатные (общие) индексы могут быть построены более сложным способом. В этих индексах представляется сумма произведений двух величин, одна из которых меняется (индексируется), а другая остаётся неизменной и в числителе, и в знаменателе (вес индекса).
Формулы агрегатных индексов.
1) Физического объёма
В случае индексов объёмных показателей весами являются качественные показатели (цена) зафиксированные на уровне базисного периода.
Разница между числителем и знаменателем индекса означает абсолютное изменение прироста или снижения товарооборота за счёт изменения физического объёма.
2) Индекс цены и других качественных показателей:
- индекс цены Пааше – сравнение цен с отчётными весами.
- Агрегатный индекс цен с базисными весами (фор-ла Ласпейроса)
ОП 10 СТАТИСТИКА
Профессиональный цикл
Основной профессиональной образовательной программы
по специальности
40.02.01 Право и организация социального обеспечения
для студентов заочной формы обучения
Разработал:
преподаватель
Е.В. Ваниева
Волгоград
АННОТАЦИЯ
Данное методическое пособие предназначено для студентов заочной формы обучения по специальности «Право и организация социального обеспечения» при изучении дисциплины «Статистика».
Рабочая программа учебной дисциплины является частью основной профессиональной образовательной программы в соответствии с ФГОС по специальности СПО 030912 Право и организация социального обеспечения. Рабочая программа составлена для очной и заочной форм обучения.
Место дисциплины в структуре основной профессиональной образовательной программы: общепрофессиональная дисциплина в профессиональном цикле
Цели и задачи дисциплины – требования к результатам освоения дисциплины:
Базовая часть:
В результате освоения дисциплины обучающийся
должен уметь:
-собирать и обрабатывать информацию, необходимую для ориентации в своей профессиональной деятельности;
-оформлять в виде таблиц, графиков и диаграмм статистическую информацию;
- исчислять основные статистические показатели;
-проводить анализ статистической информации и делать соответствующие выводы;
В результате освоения дисциплины обучающийся
должен знать:
-законодательную базу организации государственной статистической отчетности и ответственности за нарушение порядка её представления;
-современную структуру органов государственной статистики;
-источники учета статистической информации;
-экономико – статистические методы обработки учетно – статистической информации;
- статистические закономерности и динамику социально – экономических процессов.
Содержание дисциплины ориентированно на подготовку студентов к освоению профессиональных модулей ОПОП по специальности Право и организация социального обеспечения и овладению профессиональных компетенций (ПК)
ПК 1.1.Осуществлять формирование и хранение дел получателей пенсий, пособий и других социальных выплат.
СОДЕРЖАНИЕ
1.Пояснительная записка----------------------------------------------------------------4
3. Указания по выполнению контрольной работы --------------------------------5
4. Задания для выполнения контрольной работы--------------------------------12
5. Вопросы для самоконтроля и подготовки к зачету---------------------------22
6.Литература---------------------------------------------------- -------------------------23
7. Краткий курс лекций----------------------------------------------------------------24
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Контрольная работа по дисциплине «Статистика» выполняется в сроки, установленные учебным планом.
Работа выполняется одним из следующих способов:
- рукописным в обычных тетрадях;
- на печатных или графических устройствах вывода ЭВМ на листах белой писчей бумаги формата А 4.
Номер варианта контрольной работы должен соответствовать последней цифре зачетной книжки (студенческого билета).
В контрольной работе должны быть представлены: номер варианта, текст задания, подробное решение со ссылкой на формулы и их расшифровка, выводы, таблицы и графики, предусмотренные конкретным заданием.
В конце работы должен быть представлен перечень использованной литературы.
УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Перед выполнением контрольной работы необходимо изучить теоретический материал по темам: «Сводка и группировка статистических данных», «Средние величины и показатели вариации», «Выборочное наблюдение», «Ряды динамики в статистике», «Индексы в статистике».
Тема 1. Сводка и группировка статистических данных. Средние величины и показатели вариации.
Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. Величину интервала определяем по формуле(1)
i=(Xmax – Xmin) : n , (1)
где Xmах , Xmiп - соответственно максимальные и минимальные варианты признака,
п - число групп (интервалов)
Частные интервалы формируют путём последовательного прибавления к нижней границе (минимальному значению признака) величины равного интервала. Единицы изучаемой совокупности распределяют по группам в соответствии со значением признака, заключенного в каждом интервале.
По каждой группе подсчитывают частоту повторения значений изучаемого признака
Расчет средних величин и показателей вариации рекомендуется проводить в табличной форме.
Таблица 1- Группировка статистических данных
| Группы
| Частота повторения, f | Середина интервала, х1 | Расчетные показатели | ||
| x1∙f |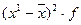 
| Sме | |||
| Итого | |||||
Среднее значение признака для сгруппированных данных рассчитывается по формуле средней арифметической взвешенной: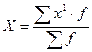 
, (2)
где х1 - среднее значение интервала, которое рассчитывается как полусумма нижней и верхней границы интервала
f- частота повторения признака
Дисперсия – средняя из квадратов отклонений вариантов значений признака от их средней величины определяется по формуле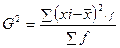(3)
(3)
Среднее квадратическое отклонение определяется по формуле 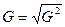(4)
(4)
Оно показывает, насколько каждое значение признака в данной совокупности отклоняется от его средней величины.
Коэффициент вариации определяется по формуле: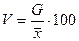 
(5)
Если коэффициент вариации более33%, то совокупность считается однородной, если менее то – неоднородной.
Структурные средние - мода и медиана определяютcя по нижеприведенным формулам:
Мода — наиболее часто встречающееся значение признака
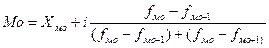, (6)
где х - нижняя граница модального интервала,
fмо, fмо-1,fмо+1 - частота повторения соответственно модального, предмодального и послемодального интервалов
Медиана — значение признака, делящее ранжированный ряд на две равные части
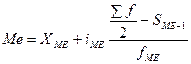, (7)
где х ме - нижняя граница медианного интервала
Sме-1 – накопленная частота интервала, предшествующего медианному.
Медианным считается интервал, накопленная частота которого превышает половину суммы всех частот.
Вариационные ряды могут быть представлены в виде полигона распределения — это ломаная линия: по оси абсцисс откладываются по значению признака, а по оси ординат — частоты, и в виде гистограммы распределения на оси абсцисс откладывают интервальные значения признака, строят прямоугольники, высота которых равна величине частот, откладываемых на оси ординат.
Дата: 2019-03-05, просмотров: 317.
