Это типичный и распространенный метод локального поиск поэтому рассмотрим его поподробнее, тем более что для случая двух переменных возможна его наглядная геометрическая интерпретация. Метод предложен Нелдером и Мидом, поэтому его час называют также по фамилии авторов.

Начнем рассмотрение с близкого ему симплексного метода (не путать с симплексным методом в линейном программировании). Он более простой, однако находит широкое применение в решении задач планирования экстремальных экспериментов.

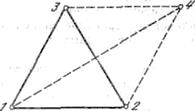
Рисунок 14. Иллюстрация идеи симплексного метода

Симплексами называют регулярные многогранники. Например, для случая двух переменных это будет равносторонний треугольник, для трех переменных - тетраэдр и т. д. Точки испытаний (рис. 14) совпадают с вершинами симплекса (точки 1, 2,3). Из вершины, в которой целевая функция максимальна (точка 1), проводится проектирующая прямая через цент тяжести симплекса. Затем строится новый симплекс, называемый отраженным, из точек 2, 3 и новой точки 4, расположенной на проектирующей прямой на надлежащем расстоянии от центра тяжести. Такая процедура в которой каждый раз вычеркивается вершина с максимально целевой функцией, повторяется. Треугольник (в случае двух переменных) как бы переворачивается через сторону с наименьшим значениями целевой функции. Существуют правила постепенного уменьшения размера симплекса и предотвращения циклического движения в окрестности минимума.

Использование именно регулярных многогранников обусловливает ряд недостатков метода: неэффективный поиск в искривленных оврагах, замедление поиска в некоторых ситуациях. В метод деформируемого многогранника симплекс может изменять свою форму, поэтому лучше приспособиться к особенностям многомерно поверхности.

Обозначим координаты вершин многогранника на /с-м шаг через

Х_i,k i = 1, . . ., п + 1; k = 0, 1, ...

Выделим вершины, в которых целевая функция максимальная и минимальная, и обозначим их соответственно через Х_плохое (Xмакс)и X_{хорошее}(X min).

(для упрощения формул индекс шага к в дальнейшем будем опускать) Через

Xцентр обозначим центр тяжести всех вершин, исключая Х_плохое:

X_n+2,j=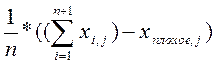

Работа метода состоит из следующих операций: отражения, растяжения, сжатия и редукции (рис. 15).

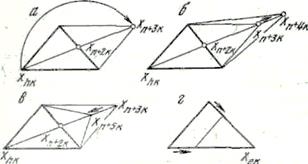
Рисунок 15. Операции метода деформируемого многогранника

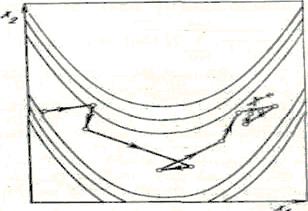
Рисунок 16. Траектория метода деформируемого многогранника

Отражение (рис. 15, а) - это проектирование точки Х_плохое через центр тяжести с получением новой точки:

Хn+з = X ( n +2)+ a *((Хn+2 — X_плохое)

где а > 0 — коэффициент отражения.

Растяжение. Если отражение прошло успешно, т. е.

/ (Х„7з) < / (х^),

то продолжаем дальше растягивать симплекс (рис. 15, б) в соответствии с соотношением

Хn+4 ⁼ Х.(n+2)+С (Хn+з — Хn+2)

где с представляет собой коэффициент растяжения. Если растяжение успешно, т. е. если

f(Хn+4) < f (X_{хорошее}), то Х_плохое заменяется на Х(т+4). В противном случае Х_плохое заменяется на Xn+3

Сжатие. Если отражение не успешно в том смысле, что f(Хn+з) > f (Xi) для всех i≠плохая, то симплекс сжимается (рис. 15, в) в сторону от центра тяжести Хn+2

Хn+5 = Х(n+2) + b* (X_плохая — Хn+2),

где 0 < b <1 — коэффициент сжатия. Х_плохая заменяется на Хn+5.

Редукция. Если сжатие не успешно в том смысле, что f (Хn+з) > f (Х_плохое), то симплекс уменьшается. Уменьшение происходит и сторону вершины с наименьшей целевой функцией X_{хорошее} (из рис.15, г). Координаты вершин пересчитываются:

Хi=Х_{хорошее}+d*(Хi-Х_{хорошее}), i=1,...,n+1.

Здесь d< 1 — коэффициент редукции.

С приближением к минимуму уменьшается и многогранник. Авторы метода предлагают следующий критерий окончания поиска:

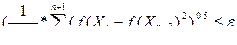
где ε- произвольно малое число, от которого зависит точности и время оптимизации.

Деформируемый многогранник адаптируется к топографии целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, сжимаясь в окрестности минимума, Он ползет по дну оврага (возможно, не так точно, как в методах Ньютона или переменной метрики) и достигает окрестностей минимума.

Конечно, стратегия метода зависит от выбора коэффициентов а, b, с, d,. В литературе можно найти следующие рекомендации по их выбору:

а = 1; b = 0,5; с = 2; d= 0,5.

Решение задач линейного программирования с помощью EXCEL

Решение задач линейного программирования с помощью ACCES

[1] (требуется воспользоваться блок-схемами приложения)

[2] Отжиг и нормализация могут быть и окончательной термической обработкой, если при этом получаются требуемые свойства материала в детали (снятие на­пряжений, перекристаллизация).