Предположим, что частные критерии оптимальности ранжированы в порядке убывания их важности. Для определенности будем считать, что каждый из них нужно максимизировать. Процедура построения компромиссного решения сводится к следующему. Сначала ищется решение, обращающее в максимум главный частный критерий оптимальности f1. Затем назначается, исходя из практических соображений и точности, с которой известны исходные данные, некоторая «уступка» Df1, которую можно допустить для того, чтобы обратить в максимум второй критерий f2.
Далее налагаем на критерий fi ограничение, чтобы он был не меньше, чем (f1( х*)-Df1. При этом ограничении ищем решение, обращающее в максимум критерий f 2.
Затем назначается уступка для критерия f2, и т.д. При таком способе нахождения компромиссного решения сразу видно, ценой какой «уступки» в одном частном критерии приобретается выигрыш в другом.
На практике используются и некоторые другие схемы компромиссов.
Использование множителей Лагранжа
При решении задач векторной оптимизации обычно вначале ищется множество эффективных неулучшаемых решений (множество Парето). Затем для принятия окончательного решения используется та или иная схема компромисса.
Сложность решения задачи во многом зависит от того, известна ли аналитическая зависимость обобщенного критерия оптимальности от частных критериев или она должна быть найдена с помощью численного эксперимента на ЭВМ.
Если функциональная зависимость обобщенного критерия от частных критериев установлена, то для решения задачи можно использовать метод неопределенных множителей Лагранжа
Рассмотрим следующую задачу векторной оптимизации:
fiopt=min fi(x), i=1,k. хÎX
Метод е-ограничений предполагает видоизменение постановки этой задачи: f1opt=min f1(x),с учетом ограничений на остальные критерии оптимальности: ei³fi(x),
где ei - максимальные допустимые (пороговые) значения критериев оптимальности, кроме первого.
Для решения задачи составляется функция Лагранжа
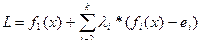
где 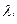 — неопределенные множители Лагранжа.
— неопределенные множители Лагранжа.
Рассмотрим два примера использования этого метода.
Пример 1.
В этой задаче используются два критерия оптимальности и две управляемые независимые переменные
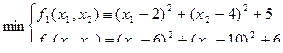
Решение.
Первая фаза решения состоит в преобразовании исходной постановки задачи:
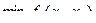 с учетом ограничения
с учетом ограничения 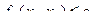
Построим функцию Лагранжа: 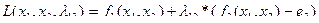
 Подставляя в нее выражения для f 1 и f2 получим
Подставляя в нее выражения для f 1 и f2 получим
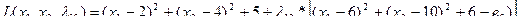
здесь  —неопределенный множитель Лагранжа.
—неопределенный множитель Лагранжа.
Найдем частные производные от функции Лагранжа по всем аргументам и приравняем их к нулю:
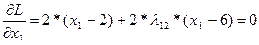
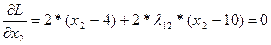
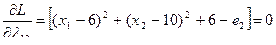
Решив систему, получим соотношение
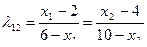
Из выражения для 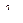 получим соотношение
получим соотношение
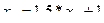
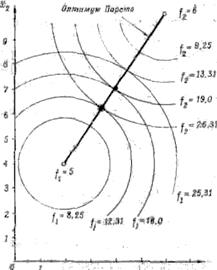
2 3 4 5 6 7 -'•t
Рисунок 9. Неулучшаемые (Парето-оптимальные) решения в пространстве управляемых переменных
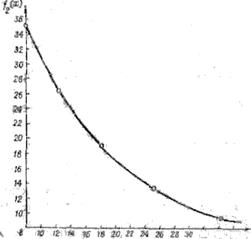
Рисунок 10. Эффективное множество компромиссов в целевом пространстве
На рис. 9 изображено множество компромиссов. Оно представляет собой отрезок прямой линии. Линии постоянного уровня каждого из критериев оптимальности являются окружностями. Отметим, что полученное решение не зависит от введенного ограничения e.
На рис.10 показано множество компромиссов в целевом пространстве.
Численные результаты решения этой задачи представлены в табл. 13.
Таблица 13
| x1 | x2 | f1 | f2 | 
|
| 2,0 | 4,00 | 5,00 | 58,00 | 0,00 |
| 2,5 | 4,75 | 5,81 | 45,81 | 0,14 |
| 3,0 | 5,50 | 8,25 | 35,25 | 0,33 |
| 3,5 | 6,25 | 12,31 | 26,31 | 0,60 |
| 4,0 | 7,00 | 18,00 | 19.00 | 1,0 |
| 4,5 | 7,75 | 25,31 | 13,31 | 1,67 |
| 5,0 | 8,50 | 34,25 | 9,25 | 3,00 |
| 5,5 | 9,25 | 44,81 | 6,81 | 7,00 |
| 6,0 | 10,00 | 57,00 | 6,00 |
Множитель Лагранжа  является функцией f1 и f2 .Это, в частности, видно на рис. 11.
является функцией f1 и f2 .Это, в частности, видно на рис. 11.
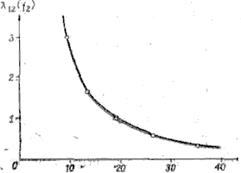
Рисунок 11. Множитель Лагранжа как функция критерия оптимальности f2
В данном простом примере решение получено в замкнутой форме. В задачах большой размерности, когда получить замкнутую форму невозможно, решение ищут путем варьирования е.
Перейдем теперь к более сложной задаче, в которой рассматриваются две управляемые переменные и три локальных критерия оптимальности.
Пример 2.
Математическая формулировка задачи имеет следующий вид:
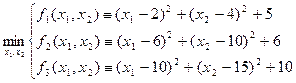
Решение.
Перепишем задачу в форме е-ограничений: 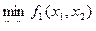 с учетом
с учетом 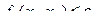
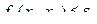 .Функция Лагранжа имеет следующий вид:
.Функция Лагранжа имеет следующий вид:
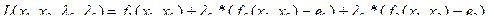
Подставляя сюда выражения для 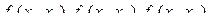 , и используя метод неопределенных множителей Лагранжа, получаем:
, и используя метод неопределенных множителей Лагранжа, получаем:
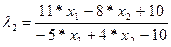
| 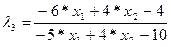
|
Заметим, что функция  не обязательно должна быть «основной», а функции
не обязательно должна быть «основной», а функции 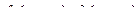 должны выполнять роль ограничений.
должны выполнять роль ограничений.
Рассматриваемая задача может быть записана в ином виде, например:
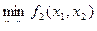 с учетом ограничений
с учетом ограничений 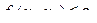 ,
, 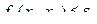
Функция Лагранжа для задачи, записанной в этой форме, имеет следующий вид:
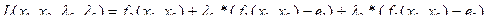
Решая эту задачу с помощью метода неопределенных множителей Лагранжа, получим:
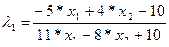
| 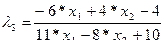
|
Результаты решения рассматриваемой задачи приведены в табл. 13.
Таблица 13
Неулучшаемые решения задачи

| 
| 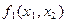
| 
| 
| 
| 
|
| 4 | 6,88 | 17,29 | 19,73 | 111.93 | 0,42 | 0,19 |
| 5 | 8,25 | 32,06 | 10,06 | 80,56 | 0,50 | 0,50 |
| 6 | 9,63 | 52,70 | 6,14 | 54,84 | 0,70 | 1,00 |
| 7 | 11,00 | 79,00 | 8,00 | 35,00 | 1,00 | 2,00 |
| 8 | 12,38 | 111,22 | 15,66 | 20.86 | 2,17 | 5,17 |

На рисунке 12 представлено множество неулучшаемых решений (множество Парето) в пространстве управляемых переменных .
Лекция 15
Дата: 2019-02-19, просмотров: 424.