Студент должен:
знать: методику определения линейных, местных и суммарных потерь напора (давления) при различных режимах движения; классификацию и методику расчета различных типов трубопроводов;
уметь: производить расчеты простых и сложных трубопроводов с построением их характеристик; определять потери напора (давления), используя соответствующие формулы, монограммы, справочники.
Режимы движения жидкости. Число Рейнольдса. Общие уравнения для определения потери напора при равномерном движении. Распределение скоростей при ламинарном и турбулентном режимах по живому сечению потока. Влияние различных факторов на коэффициент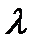 
. Формула для определения коэффициента 
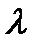. Потеря напора в трубах некруглого сечения. Местное сопротивление. Коэффициенты местных сопротивлений сложение потерь напора. Возможные способы снижения потерь напора в трубах. Сопротивление при обтекании тел. Движение твердых тел в восходящем потоке жидкости.
Назначение и классификация трубопроводов. Основные формулы для расчета трубопроводов. Основные задачи при проектировании и расчете трубопроводов. Расчет простого и сложного трубопровода. Графоаналитические методы расчета.
Практическая работа №2
Гидравлический расчет трубопроводов.
Вопросы для самоконтроля
1. Перечислите виды гидравлических сопротивлений, возникающих при движении жидкости.
2. В чем состоит отличие турбулентного режима от ламинарного?
3. Что такое число Рейнольдса. Написать аналитическое выражение для определения числа Re для потока в трубе круглого сечения.
4. Что такое относительная и абсолютная шероховатость?
5. Как определить потерю напора при ламинарном режиме в трубах?
6. От каких факторов зависит коэффициент гидравлического трения при турбулентном режиме в трубах и по каким формулам можно его найти?
7. Написать формулу Шези и объяснить все входящие в нее величины.
8. Какие сопротивления называются местными? По каким формулам можно найти их величину?
Методические указания
В этой теме необходимо разобрать уравнение равномерного движения жидкости и формулу Шези. Затем перейти к изучению гидравлических сопротивлений, встречающихся при движении жидкости.
Так как гидравлические сопротивления в значительной мере зависят от режима движения жидкости, то изучение их целесообразно начинать с ознакомления с ламинарного и турбулентного режима движения.
Нужно представлять физический смысл числа Рейнольдса, знать его критерии, который дает возможность практически установить переход ламинарного режима в турбулентный.
При изучении потерь напора на преодоление местных сопротивлений следует знать причины, вызывающие местные потери напора и усвоить общую зависимость для этих потерь
Важно уяснить, что из всего разнообразия трубопроводов, их гидравлический расход может быть сведен к трем принципиальным схемам:
1.Расчет простого короткого трубопровода при постоянном расходе, когда детально учитываются сопротивления по длине, местные сопротивления и величина скоростного потока.
2.Расчет простого длинного трубопровода при постоянном расходе, когда точно учитываются сопротивления по длине, а величина местных сопротивлений определяется приближенно ( в процентах от потерь напора по длине 5-15%).
3.Расчет простого длинного трубопровода с транзитным и равномерно распределенным путевым расходом.
Для первых двух систем трубопровода необходимо усвоить:
1.Вывод расчетной зависимости для общего случая турбулентного движения жидкости (независимо от зон сопротивлений).
2.Преобразование этой зависимости введением расходной характеристики для квадратичной зоны сопротивлений.
Таким преобразованием формула приводится к виду, удобному для технических расчетов.
Для третьей схемы трубопроводов нужно рассмотреть вопрос определения расчетного расхода.
Необходимо научиться пользоваться специальными таблицами и монограммами, в которых даны значения гидравлических уклонов в зависимости от величины расхода для стандартных размеров сечения трубопроводов. Они упрощают и ускоряют расчеты. Рассмотреть явление гидравлического удара в трубопроводе постоянного сечения большой длины.
| Рис. 26. |
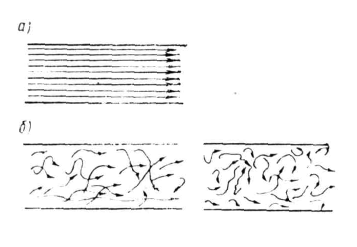В зависимости от рода жидкости, скорости ее движения и характера стенок, ограничивающих поток, различают два основных режима движения: ламинарный и турбулентный. Ламинарным называют упорядоченное движение, когда отдельные слои скользят друг по другу, не перемешиваясь (рис. 26, а).
Ламинарный режим движения можно наблюдать чаще у вязких жидкостей, таких как нефть, масла и т. п.
Турбулентным называют режим, при котором наблюдается беспорядочное движение, когда частицы жидкости движутся по сложным траекториям и слои жидкости постоянно перемешиваются друг с другом (рис. 26, б).
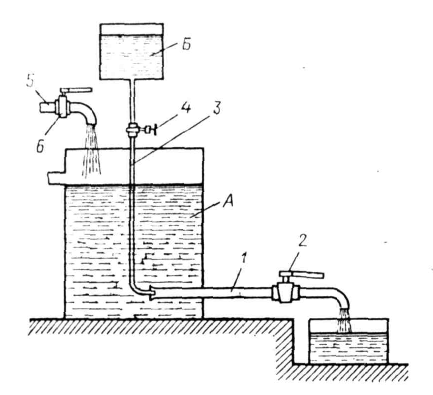
| Рис. 27. |
Достаточно полные лабораторные исследования режимов движения и вопрос их влияния на характер зависимости потерь напора от скорости впервые исследовал английский физик Рейнольдс.
Установка Рейнольдса для исследования режимов движения жидкости пред ста влена на рис. 27. Сосуд А заполняется испытуемой жидкостью. К сосуду А в нижней его части присоединена стеклянная трубка 1 с краном 2, которым регулируется скорость течения в трубке. Над сосудом А расположен сосуд Б с раствором краски. От сосуда Б отходит трубка 3 с краном 4. Конец трубки 3 заведен в стеклянную трубку 1. Для пополнения сосуда А служив трубка 5 с запорным устройством 6.
При ламинарном режиме движения жидкости по трубке 1 струйка раствора краски, истекающей из трубки 3, имеет вид четко вытянутой нити вдоль трубки 1.
По мере открытия крана 2 увеличивается скорость движения и режим движения переходит в турбулентный, при этом струйка приобретает волнообразный характер, а при еще большей скорости совсем размывается и смешивается с жидкостью в трубке. При постепенном закрытии крана эти явления протекают в обратном порядке, т. е. турбулентный режим сменяется ламинарным.
Опыты показали, что переход от турбулентного режима к ламинарному происходит при определенной скорости (эта скорость называется критической), которая различна для разных жидкостей и диаметров труб; при этом критическая скорость растет с увеличением вязкости жидкости и с уменьшением диаметра труб.
Рейнольдсом и рядом других ученых опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее основные характеристики потока
,
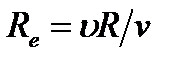где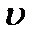 
– скорость, м/с;
R - гидравлический радиус, м;
v - кинематический коэффициент вязкости, м2/сек.
Это отношение называется числом Рейнолъдса. Значение числа Re , при котором турбулентный режим переходит в ламинарный, называют критическим числом Рейнолъдса ReKp .
Если фактическое значение числа Re , вычисленного по формуле (82), будет больше критического Re > ReKp – режим движения турбулентный, когда Re < ReKp – режим ламинарный.
Для напорного движения в цилиндрических трубах удобнее число Рейнольдса определять по отношению к диаметру d , т. е.
,
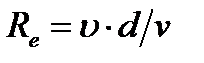где d – диаметр трубы.
В этом случае ReKp получается равным ~2300. Если в формуле для трубопроводов круглого сечения d выразить через гидравлический радиус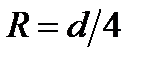 
, то получим ReKp =575. Для других трубопроводов и каналов некруглых сечений можно принимать значение критического числа Рейнольдса ReKp=300 (при вычислении Re через гидравлический радиус).
Дата: 2019-02-19, просмотров: 484.
