Рис1.9,а Рис1.9,б
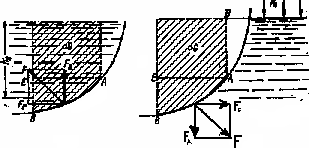
(Рис. 1.9) Схема для определения силы давления жидкости на цилиндрическую поверхность
1) жидкость расположена сверху (рис. 1.9, а);
2) жидкость расположена снизу (рис. 1.9, б).
Сила гидростатического давления на криволинейную поверхность определяется по теореме Пифагора:
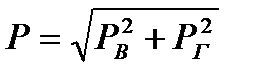
Рв и Рг – вертикальная и горизонтальная составляющая силы
Горизонтальная составляющая равна силе давления на вертикальную проекцию криволинейной поверхности:
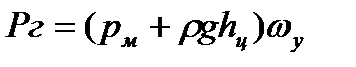
рм – манометрическое давление на поверхности жидкости
hц – глубина погружения центра тяжести вертикальной проекции криволинейной поверхности
ωy – площадь вертикальной проекции
Вертикальная составляющая равна весу жидкости в объеме тела:
Рв = ρgV
Определение толщины стенки трубы или резервуара.
| А |
| В |
| l |
| δ |
| d |
| Px |
| Px |
Рассмотрим поперечное сечение цилиндрической трубы длиной l диаметром d. Стенки трубы подвержены внутреннему давлению р жидкости или газа, которое примем постоянным во всех точках.
Под действием давления р труба стремится разорваться, например, по плоскости АВ. Разрывающая сила Px определяется как горизонтальная составляющая на криволинейную поверхность без учета собственного веса жидкости:
Px = pωy
ωy = ld – площадь вертикальной проекции внутренней поверхности трубы
Разрывающей силе сопротивляется материал трубы.
Сила сопротивления:
P = 2δlσ
δl – площадь сечения
σ – допускаемое напряжение на разрыв материала стенки трубы.
Условие не разрыва стенки трубы: Px = P, т.е.
pωy = 2δlσ, отсюда
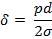
Это значение увеличиваем на производственный припуск 3…7 мм.
Задача 2. Горизонтальная металлическая цистерна круглого сечения с диаметром 2м и длиной 10 м заполнена минеральным маслом плотностью 917,4 кг/м3. Давление на поверхности масла равно атмосферному. Определить силу давления на внутреннюю криволинейную поверхность.
| Дано: d = 2 м l = 10 м р = 917,4 кг/м3 p а = 98,1 кПа Р - ? | Решение:
Р = √ Р2х + Р2у
Рх = ρghцωу = 917,4 х 9,8 х 1x 20 = 180 кН
hц = 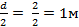 ωу = dl = 2x10 = 20 м
Ру = рgV = 917,4 х 9,8 х 15,7 = 141,3 кН
V =
ωу = dl = 2x10 = 20 м
Ру = рgV = 917,4 х 9,8 х 15,7 = 141,3 кН
V = 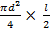 = = 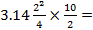 15.7 м3
Р = √ 1802 + 141,32 = 230 кН 15.7 м3
Р = √ 1802 + 141,32 = 230 кН
|
Задача 3. Стальная труба диаметром 400 мм находится под давлением 16 х 105 Па. Определить толщину стенок трубы, если допускаемое напряжение на разрыв для стали 16 х 107 Па.
| Дано: d = 400 мм p = 16 х 105 Па σ = 16 х 107 Па | Решение
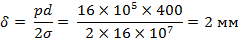
|
δ - ?
Вопросы для самоконтроля
1. Что такое гидростатическое давление в данной точке?
2. Что называется абсолютным давлением, избыточным давлением и вакуумом?
3. Какими приборами можно измерить гидростатическое давление?
4. Что такое пьезометрическая высота и гидростатический напор?
5. Как определить величину силы гидростатического давления на плоскую стенку? Дать схему изображения.
6. Что такое центр давления и как его определить?
7. Как определить величину, направление и точку приложения силы гидростатического давления на криволинейную стенку?
Тема 1.4. Общие законы и уравнения статики и динамики жидкостей и газов.
Студент должен:
знать: законы Архимеда и Паскаля; основные понятия и определения, уравнения гидродинамики; геометрический и энергетический смысл уравнения Бернулли, его практическое применение; принцип действия приборов для измерения скорости и расхода жидкости; законы истечения, назначение и типы насадков; , основы расчета гидравлического удара
уметь : применять уравнения: расхода, неразрывности потока Бернулли при решении практических задач, применять законы гидростатики для решения практических задач, определять скорость, расход, время истечения жидкости из отверстий и насадков, давление струи жидкости на преграду.
Закон Архимеда и закон Паскаля.Задачи, основные законы и уравнения статики и динамики. Гидравлические элементы потока. Уравнение Бернулли для идеальной жидкости. Энергетический и геометрический смысл уравнения Бернулли. Примеры практического применения уравнений гидродинамики. Измерение расхода и скорости.
Истечение жидкости через малое отверстие в тонкой стенке. Истечение жидкости при переменном напоре. Истечение жидкости под уровень истечение жидкости из насадков. Влияние числа Рейнольдса на истечение жидкости. Давление струи жидкости на преграду. Практическое применение насадков.
Вопросы для самоконтроля
1. В чем состоит закон Архимеда?
2. В чем состоит закон Паскаля?
3. Какими признаками характеризуется истечение жидкости из отверстия в тонкой стенке сосуда?
4. При каких условиях короткую трубу можно рассматривать как внешнюю цилиндрическую насадку?
5. Формулы скорости и расхода для истечения жидкости из отверстия и через насадки.
6. Как связаны между собой коэффициенты скорости - 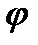 , сжатия -
, сжатия - 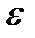 , расхода -
, расхода - 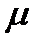 .
.
7. Какая форма насадки обеспечивает наибольший расход при заданной величине отверстия в стенке сосуда?
8. При каких условиях в трубопроводе возникает гидравлический удар?
9. Как определяется повышение давления при гидравлическом ударе?
10. В чем состоит геометрический и энергетический смысл уравнения Бернулли?
Практическое занятие №1.
Расчет силы гидростатического давления, расхода жидкости и скорости истечения.
Методические указания
К простым гидростатическим машинам относятся гидравлический пресс, гидравлический домкрат, гидравлический аккумулятор, гидравлический мультипликатор и т. д. они используются для создания больших сил давления при помощи жидкости. Их работа основана на применении закона Паскаля.
При изучении каждого типа пропускных отверстий (отверстий в тонкой стенке, насадки) необходимо вначале рассмотреть классификацию их, а затем уже расчетные формулы для определения скорости истечения и расхода. При выводе указанных расчетных формул используются основные уравнения гидравлики: уравнение Бернулли и уравнение неразрывности потока, причем учитываются потери напора (главным образом местные).
Для насадков надо усвоить расчет гидродинамического давления в сжатом сечении, обратить внимание на предельное значение напора, выше которого насадка перестает работать.
Для истечения через отверстие с острой кромкой и с насадкой характерно отсутствие значительных потерь по длине и относительное постоянство для каждого наасдка коэффициентов местного сопротивления, а отсюда и коэффициентов скорости 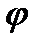 и расхода
и расхода 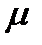
Дата: 2019-02-19, просмотров: 471.