Система n линейных уравнений с n переменными (общий вид). Матрица системы. Матричная форма записи системы. Совместные (определенные и неопределенные) и несовместные системы. Теорема Крамера о разрешимости системы n линейных уравнений с n переменными (без доказательства). Решение системы: по формулам Крамера; с помощью обратной матрицы; методом Гауса. (1, гл. 2, §2.1—2.3,2.6; с. 38—47,53—56); (2, гл. 2).

      При изучении материала темы следует освоить матричную форму записи заданной системы п линейных уравнений с п переменными и уметь переходить к этой форме от общего вида системы и наоборот. Необходимо знать и уметь объяснить, какие системы уравнений называются совместными (определенными и неопределенными) и несовместными. Надо твердо уяснить, что вопрос о разрешимости системы n линейных уравнений с n переменными устанавливается с помощью теоремы Крамера (1, с. 41); решаются же такие системы различными способами: по формулам Крамера, с помощью обратной матрицы и методом Гаусса (см. примеры 2.1 – 2.3, 2.6, 2.7).

    Наиболее важен для практики метод Гаусса, имеющий по сравнению с другими способами решения ряд достоинств: он менее трудоемок, позволяет однозначно установить, является ли данная система определенной, неопределенной или несовместной, а в случае совместности системы – определить число ее независимых уравнений и исключить «лишние».

     В методе Гаусса нужно усвоить правило исключения неизвестных х₁, х₂, …, х_n-1. Сначала умножается первая строка на соответствующие коэффициенты. Цель – в первом столбце во всех строках кроме первой обеспечить нули путем прибавления первой строки, умноженной на коэффициенты, ко второй и последующим строкам.

     Затем умножается вторая строка на соответствующие коэффициенты. Цель – обеспечить нули во втором столбце во всех строках кроме второй (a₂₂ ¹0) путем прибавления к третьей и последующим строкам второй строки, умноженной на необходимые коэффициенты и т.д.

     Для первой строки это коэффициенты (-a₂₁/a₁₁;-a₃₁/a₁₁;…;-a_m1/a₁₁); для второй строки это коэффициенты (-a₃₂/a₂₂;-a₄₂/a₂₂;…;-a_m2/a₂₂).

Необходимо понять, что при прямом ходе решения системы уравнений методом Гаусса определяется неизвестное х_n. Затем при обратном ходе определяются х_n-1, х_n-2 и так до х₁.

Необходимо уяснить, что метод Гаусса менее трудоемок особенно при решении систем уравнений более четвертого порядка.

Следует обратить внимание на различие между основными или базисными переменными, для которых определитель матрицы из коэффициентов при них отличен от нуля (х₁,х₂,…,х_r—переменные). Остальные (n–r) переменных называются не основными или свободными.

Необходимо усвоить, что для базисных решений должны быть равны нулю все (n-r) не основных переменных, и что число базисных решений имеется не более С_n^r = .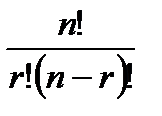

Необходимо разобраться (теорема Кронекера-Капелли) в том, что система имеет единственное решение в том случае, когда ранг матрицы «r» равен числу переменных «n», т.е. r=n; система имеет бесконечное множество решений, если n >r.

Необходимо разобраться в алгоритме нахождения базисных решений, а именно: научиться находить все определители, не равные нулю, которые и составляются из коэффициентов при основных (базисных) переменных, выражать основные (базисные) решения через не основные. Иметь понятие о функциональной системе решений для системы линейных однородных уравнений.

     Рекомендуется разобрать задачи с решениями N 2.1 – 2.3, 2.6, 2.7 и задачи ля самостоятельной работы N 2.11, 2.12, 2.15 – 2.18, 2.21 – 2.23 по учебнику [1] и аналогичные задачи по практикуму [2].

Тема 3 Векторы

Векторы на плоскости и в пространстве (сложение, вычитание, умножение на число). Координаты и длина вектора, п-мерный вектор. Линейная комбинация, линейная зависимость и независимость векторов. Понятие о векторном (линейном) пространстве и его базисе. Собственные векторы и собственные значения матрицы. Характеристический многочлен матрицы. (1, гл. 3, § 3.1 – 3.3, 3.7; с. 63 – 66, 68 – 72, 82 – 84); (2, гл. 3).

Необходимо рассмотреть и усвоить понятие вектора, обозначения векторов, определение длины векторов, определение коллинеарных векторов, противоположных векторов. Изучить операции сложения и вычитания векторов на плоскости и в пространстве. Правило параллелограмма, многоугольника, параллелепипеда.

Надо уяснить, что скалярное произведение векторов это произведение модулей их длин на косинус угла между ними, а скалярное произведение в координатах равно сумме произведений соответствующих координат. Разобрать задачи с решениями (1,3.14–3.17).

Необходимо разобраться с понятием n-мерного вектора и векторного пространства, изучить свойства векторного пространства.

Множества всех плоских и пространственных векторов, для которых определены операции сложения и умножения, а также умножения вектора на число, являются простейшими примерами векторных пространств. В данной теме обобщается понятие вектора и дается определение векторного пространства.

Необходимо уяснить понятие линейной комбинации, линейной зависимости и линейной независимости векторов, а именно: линейная комбинация векторов a₁,a₂,…,a_n векторного пространства R равна сумме произведений этих векторов на произвольные действительные числа (a_m=l₁a₁+l₂a₂+…+l_m-1a_m-1). Линейно зависимые векторы (как и строки матрицы) - это такие векторы, для которых существуют такие числа l₁,l₂,…,l_m не равные нулю одновременно такие, что l₁a₁+l₂a₂+…+l_ma_m=0. Линейно независимые - это вектора, для которых l₁a₁+l₂a₂+…+l_ma_m=0 возможно только при одновременном равенстве нулю всех чисел l₁=l₂=…=l_m=0.

В случае линейной зависимости векторов, по крайней мере, один из них выражается через остальные.

Необходимо уяснить, что любой вектор пространства может быть представлен в виде линейной комбинации векторов базиса.

      Особую роль в приложениях математики играют векторы, обладающие следующим свойством: при умножении квадратных матриц на них образуются новые векторы, коллинеарные исходным. Такие векторы получили название собственных векторов матрицы, а соответствующие им числа – собственных значений матрицы. Точное определение собственных векторов и значений приведено в (1, с. 82).

      Рекомендуется разобрать задачи с решениями N 3.2, 3.3, 3.7 и задачи для самостоятельной работы N 3.18 – 3.20, 3.27, 3.28 по учебнику (1) и аналогичные задачи по практикуму (2).

РАЗДЕЛ II ВВЕДЕНИЕ В АНАЛИЗ

Тема 4 Функции

Понятие о множествах. Действительные числа и числовые множества. Постоянные и переменные величины. Функции и способы их задания. Область определения функции. Четные, нечетные, монотонные и ограниченные функции. Сложная функция. Понятие элементарной функции. Основные элементарные функции и их графики. Неявные функции. ( гл. 4, § 4.1 – 4.3, 4.6; с. 95 – 99, 100 – 103,.115 – 117); (2, гл. 5,4).

Прежде всего, полезно ознакомиться с некоторыми логическими символами и кванторами, чтобы использовать их в дальнейшем для сокращения записей (1, с. 123).

      Изучение темы следует начать с основных понятий теории множеств , [1, с. 123 – 124]. Далее нужно четко усвоить важнейшее понятие математического анализа – функции, уметь находить область ее определения, знать три способа задания функции: аналитический, графический, табличный.

 Студенту нужно знать простейшие преобразования для построения функций, как-то: сдвиг графика y=f(x+a)+b вправо при а < 0 и влево при a > 0, а также на 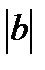 параллельно оси Ох вниз при b< 0 и вверх на  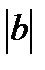при b >0; сжатие 0<m<1 (растяжение m >1) графика функции y=m×f(x) вдоль оси Ох.

 В курсе рассматриваются в основном элементарные функции. Студент должен уяснить определение элементарной функции (1, с. 132) четко знать свойства и строить графики следующих основных элементарных функций:                 у=С (постоянная), у= xⁿ (степенная), у=a^x (показательная), у=log_ax (логарифмическая). Необходимо усвоить понятие сложной функции (функции от функции).

 Построение графика четной (нечетной) функции можно значительно упростить, если учесть, что графики четных функций симметричны относительно оси Оу, а нечетных – относительно начала координат. Одним из характерных свойств функции является монотонность (т.е. возрастание или убывание на каком-либо промежутке).

Студенту необходимо уяснить, что функции находит широкое применение в экономической теории. Знать конкретные виды функций и их сущность (функция полезности, функция издержек и т.д.).

Уравнение линии на плоскости. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой. Уравнение прямой, проходящей через данную точку в заданном направлении, через две данные точки. Условия параллельности и перпендикулярности двух прямых. Точка пересечения двух прямых. (1, гл. 5, § 5.1–5.5, 5.7, с. 123–132, 138, 139).

Студенту необходимо прочно усвоить материал, который будет использован при изучении экономико-математических методов и прикладных моделей (линейное программирование). Большое значение здесь имеет определение уравнения линии на плоскости как уравнения с двумя переменными х и у, которому удовлетворяют координаты каждой точки этой линии и не удовлетворяют координаты любой точки, не лежащей на ней. Из этого определения следуют два важных для практики положения, которые нужно знать:

1. Если задано уравнение линии, то можно установить, принадлежит ли ей какая-либо точка плоскости. Для этого достаточно подставить координаты точки в уравнение линии вместо переменных х и у. Если окажется, что они удовлетворяют уравнению, то точка принадлежит линии, в противном случае – не принадлежит.

       2. Координаты точки пересечения двух линий, заданных своими уравнениями, удовлетворяют обоим уравнениям. Поэтому для нахождения координат точки пересечения двух линий нужно решить систему, составленную из их уравнений. Этот вопрос должен быть усвоен твердо.

Студент должен знать простейшие виды уравнений прямой и уметь пользоваться ими при решении задач. Соответствующий учебный материал приведен в (1, с.95–99, 100–103,115–116).

Обратите особое внимание на нахождение уравнений прямых, параллельной и перпендикулярной данной прямой (пример 4.5).

Рекомендуется разобрать задачи с решениями N4.1–4.3, 4.5, 4.10, 4.12 и задачи для самостоятельного решения N 4.14–4.19, 4.21–4.23 по учебнику (1) и аналогичные задачи по практикуму (2).