При течении газа (жидкости) в канале для любого его сечения справедливо уравнение (1.119) (аналогично (1.114)):
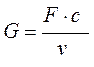 , (1.119)
, (1.119)
где 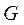 - постоянный массовый расход газа, кг/с;
- постоянный массовый расход газа, кг/с; 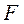 - площадь сечения канала, м2;
- площадь сечения канала, м2; 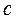 - скорость газа, м/с;
- скорость газа, м/с; 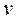 - удельный объём газа в данном сечении канала, м3/кг.
- удельный объём газа в данном сечении канала, м3/кг.
Из соображения неразрывности потока при стационарном режиме течения расход газа одинаков в любом сечении потока, т.е.
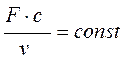 . (1.120)
. (1.120)
В гидродинамике это уравнение называется уравнением неразрывности. Проведя ряд преобразований, это уравнение можно привести у виду:
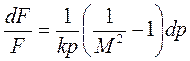 , (1.121)
, (1.121)
где 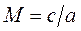 - число Маха (отношение скорости течения к местной скорости звука). Значение
- число Маха (отношение скорости течения к местной скорости звука). Значение 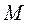 <1 соответствует течению с дозвуковой скоростью (
<1 соответствует течению с дозвуковой скоростью ( 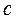 <
< 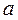 ), а
), а 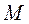 >1 – течению со скоростями, превышающими скорость звука (
>1 – течению со скоростями, превышающими скорость звука ( 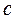 >
> 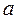 ).
).
Уравнение (1.121) связывает изменение площади поперечного сечения канала (при адиабатном течении без трения и без совершения технической работы) с изменением давления в потоке и с числом Маха. Преобразуя это уравнение, получим уравнение, связывающее изменение площади сечения канала с изменением скорости потока и с 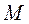 :
:
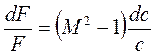 , (1.122)
, (1.122)
Анализ уравнений (1.121) и (1.122) приведен в таблице:
| Вид потока | Вид канала | |
| Сопло (ускорение потока, падение давления вдоль потока) | Диффузор (торможение потока, увеличение давления вдоль потока) | |
Дозвуковой ( 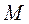 <1) <1)
| Суживающийся | Расширяющийся |
Сверхзвуковой ( 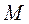 >1) >1)
| Расширяющийся | Суживающийся |
Из таблицы видно, для дальнейшего ускорения потока, достигшего на выходе из суживающегося сопла звуковую скорость, сопло должно быть спрофилировано так, чтобы канал суживался до тех пор, пока давление в канале не станет равным критическому давлению истечения 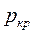 , а скорость потока станет звуковой. За этим сечением канал должен быть выполнен расширяющимся. Поток перейдет через скорость звука и будет продолжать ускоряться в расширяющейся части сопла.
, а скорость потока станет звуковой. За этим сечением канал должен быть выполнен расширяющимся. Поток перейдет через скорость звука и будет продолжать ускоряться в расширяющейся части сопла.
Такое комбинированное сопло получило название сопло Лаваля. На рисунке 21 показан разрез сопла Лаваля. Здесь же представлен график распределения скорости потока и местной скорости звука по длине сопла.
Сопло Лаваля рассчитывается таким образом, чтобы давление в выходном сечении сопла 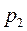 было равно давлению среды
было равно давлению среды 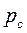 . Длина суживающейся части сопла выбирается минимальной. Длина расширяющейся, сверхзвуковой части сопла, имеет коническую форму с углом раствора сопла
. Длина суживающейся части сопла выбирается минимальной. Длина расширяющейся, сверхзвуковой части сопла, имеет коническую форму с углом раствора сопла 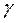 не более 11-12° (при больших углах раствора возникает опасность отрыва потока от стенок сопла).
не более 11-12° (при больших углах раствора возникает опасность отрыва потока от стенок сопла).
1.20 Истечение из сопла водяного пара. Расчёт процесса истечения с помощью 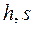 - диаграммы. Истечение без трения. Действительный процесс истечения
- диаграммы. Истечение без трения. Действительный процесс истечения
Водяной пар не является идеальным газом, поэтому расчёт его истечения лучше выполнять не по аналитическим формулам, а по 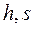 - диаграмме (рисунок 22).
- диаграмме (рисунок 22).
Пар с начальными параметрами 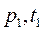 вытекает в среду с давлением
вытекает в среду с давлением 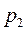 . Если пренебречь потерями энергии на трение при движении водяного пара по каналу и теплоотдачей к стенкам сопла, то процесс истечение протекает при постоянной энтропии и изображается на
. Если пренебречь потерями энергии на трение при движении водяного пара по каналу и теплоотдачей к стенкам сопла, то процесс истечение протекает при постоянной энтропии и изображается на 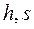 - диаграмме вертикальной прямой 1-2.
- диаграмме вертикальной прямой 1-2.
Скорость истечения рассчитывается по формуле (1.112):
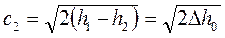 , (1.112)
, (1.112)
где 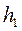 - начальная энтальпия, определяемая как точка пересечения линий
- начальная энтальпия, определяемая как точка пересечения линий 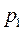 и
и 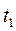 ;
;
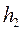 - конечная энтальпия, находящаяся на пересечении вертикали, проведенной из точки 1, с изобарой
- конечная энтальпия, находящаяся на пересечении вертикали, проведенной из точки 1, с изобарой 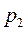 (точка 2).
(точка 2).
В реальных условиях из-за трения потока о стенки канала процесс истечения оказывается неравновесным, т.е. при течении газа выделяется теплота и поэтому энтропия рабочего тела возрастает.
На рисунке 22 неравновесный процесс расширения изображен условно штриховой линией 1-2´. При этом же перепаде давлений 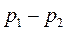 срабатываемая разность энтальпий
срабатываемая разность энтальпий 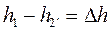 получается меньше, чем
получается меньше, чем 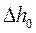 . В результате этого уменьшается и скорость истечения
. В результате этого уменьшается и скорость истечения 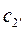 . Часть кинетической энергии потока из-за трения переходит в теплоту, а скоростной напор
. Часть кинетической энергии потока из-за трения переходит в теплоту, а скоростной напор 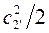 на выходе из сопла получается меньше, чем при отсутствии трения. Потеря в сопловом аппарате кинетической энергии вследствие трения выражается разностью
на выходе из сопла получается меньше, чем при отсутствии трения. Потеря в сопловом аппарате кинетической энергии вследствие трения выражается разностью 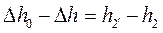 . Отношение потерь в сопле к располагаемому теплопадению называется коэффициентом потери энергии в сопле
. Отношение потерь в сопле к располагаемому теплопадению называется коэффициентом потери энергии в сопле 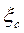 :
:
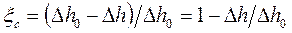 . (1.123)
. (1.123)
Преобразуя выражение (1.123) для выражения из него 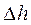 и подставив его значение в (1.112), получим:
и подставив его значение в (1.112), получим:
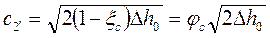 . (1.124)
. (1.124)
Коэффициент 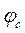 называется скоростным коэффициентом сопла. Современные сопла имеют
называется скоростным коэффициентом сопла. Современные сопла имеют 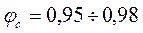 .
.
Дата: 2019-02-19, просмотров: 431.