Рассмотрим процесс равновесного (без трения) адиабатного истечения газа через сопло из резервуара, в котором газ имеет параметры 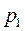, , 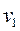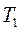. Скорость газа на входе в сопло обозначим через 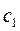. Примем, что давление газа на выходе из сопла  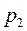равно давлению среды, в которую вытекает газ. расчет сопла сводится к определению скорости и расхода газа на выходе из него, нахождению площади поперечного сечения и правильному выбору его формы.

Скорость истечения в соответствии с уравнением (1.110)

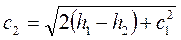                                          .                            (1.111)

Для достаточно большой площади входного сечения сопла 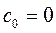 скорость истечения можно определить:

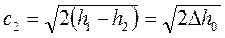                                ,                          (1.112)

где 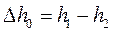 - располагаемый адиабатный теплоперепад.

Проведя ряд преобразований для адиабатного процесса уравнение (1.112) преобразуется к виду:

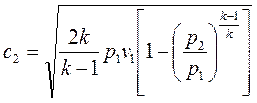                             .                        (1.113)

Массовый расход газа через сопло (кг/с) определяется из соотношения

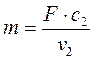                                                 ,                                      (1.114)

где 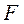 - площадь выходного сечения сопла.

Используя выражения (1.114) и (1.113), получим

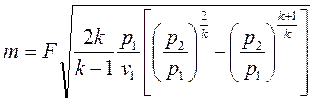                           .                  (1.115)

Из уравнения (1.115) следует, что массовый расход идеального газа при истечении зависит от площади выходного сечения сопла, свойств и начальных параметров газа ( 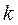, , 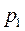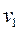) и степени его расширения (т.е. давления  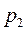газа на выходе).

По уравнению (1.115) построена кривая  на рисунке 20.

При 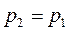 расход равен нулю. С уменьшением давления среды  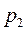расход газа увеличивается и достигает максимального значения при 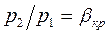. При дальнейшем уменьшении отношения  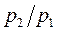значение 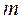, рассчитанное по формуле (1.115), убывает и при  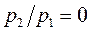становится равным нулю.

Эксперимент показал, что для 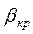< <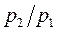1 результаты полностью совпадают, а для 0< 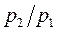<  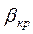они расходятся – действительный массовый расход на этом участке остается постоянным (прямая 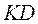). Таким образом, в суживающемся сопле невозможно получить давление газа ниже некоторого критического значения 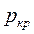, соответствующего максимальному расходу газа через сопло. Как бы ни понижалось давление среды 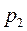, куда происходит истечение, давление на выходе из сопла остается постоянным и равным .

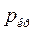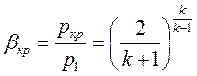                                       .                            (1.116)

Отношение критического давления на выходе 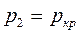 к давлению перед соплом  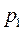имеет постоянное значение и зависит только от показателя адиабаты, т.е. от природы рабочего тела:

Газ	1-атомный	2-атомный	3-атомный и перегретый пар
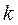
	1,66	1,4	1,3
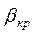
	0,49	0,528	0,546

Критическая скорость устанавливается в устье сопла при истечении в окружающую среду с давлением, равным или ниже критического. Её можно определить из уравнения (1.113), подставив в него вместо отношения 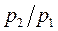 значение :

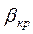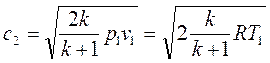                              .                        (1.117)

Величина критической скорости определяется физическими свойствами и начальными параметрами газа.

Проведя ряд преобразований, уравнение (1.117) преобразуется:

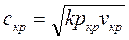                                               .                                 (1.118)

Известно, что 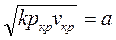- скорость распространения звука в среде с параметрам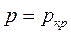и  и .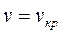

Таким образом, критическая скорость газа при истечении равна местной скорости звука в выходном сечении сопла.