Действительно существующие газы можно считать идеальными при высоких температурах и малых давлениях.

В газах, находящихся в состояниях, близких к сжижению, нельзя пренебречь объёмом молекул и силами притяжения между ними. Такие газы к идеальным не относятся, и их называют реальными газами.

Для равновесной термодинамической системы существует функциональная связь между параметрами состояния, которая называется уравнением состояния:

.

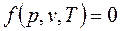Уравнение состояния можно представить в виде

.

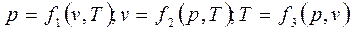Эти уравнения показывают, что из трёх основных параметров, определяющих состояние системы, независимыми являются два любых.

Выведем уравнение состояния идеального газа.

Из уравнений (1.1) и (1.4) следует, что

.

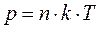Рассмотрим 1 кг газа. Учитывая, что в нем содержится 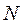молекул, и, следовательно, 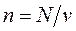, получим:

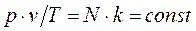
Постоянную величину 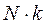, отнесенную к 1 кг газа, обозначают буквой  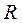и называют характеристической газовой постоянной. Поэтому

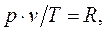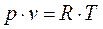                                  или ,                            (1.5)

Соотношение (1.5) - уравнение Клапейрона.

Умножив (1.5) на 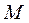, получим уравнение состояния для произвольной массы газа 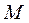кг:

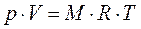                                             .                                     (1.6)

Уравнение Клапейрона можно перевести в универсальную форму, если отнести газовую постоянную к одному киломолю газа, т.е. к количеству газа, масса которого в килограммах численно равна молекулярной массе 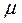. Примем в уравнении (1.6)  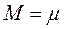и , тогда получим для одного моля:

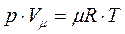                                               .                                      (1.7)

Здесь 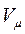 - объём одного киломоля газа, а  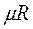- универсальная газовая постоянная.

Уравнение (1.7) - уравнение Менделеева-Клапейрона.

По закону Авогадро объём одного моля, одинаковый в одних и тех же условиях для всех идеальных газов, при нормальных физических условиях равен 22,4 м³/кмоль, поэтому

.

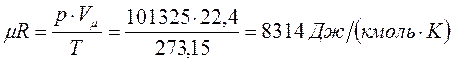Газовая постоянная одного килограмма газа

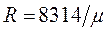                                                   .                                     (1.8)

В реальных газах в отличие от идеальных существенны силы межмолекулярных взаимодействий (силы притяжения, когда молекулы находятся на значительном расстоянии, и силы отталкивания при достаточном сближении их друг с другом) и нельзя пренебречь собственным объемом молекул.

Свободный для движения молекул объём будет равен 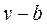, где 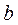 - тот наименьший объём, до которого можно сжать газ.

Силы притяжения действуют в том же направлении, что и внешнее давление, и приводят к возникновению молекулярного (или внутреннего) давления 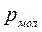. Сила молекулярного притяжения пропорциональна квадрату плотности газа, поэтому молекулярное давление обратно пропорционально квадрату удельного объёма:

,

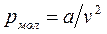где 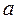 - коэффициент пропорциональности, зависящий от природы газа.

Уравнение Ван-дер-Ваальса – одно из уравнений состояния реального газа:

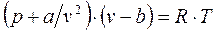                                  .                              (1.9)

При больших удельных объёмах и сравнительно невысоких давлениях реального газа уравнение Ван-дер-Ваальса переходит в уравнение Клапейрона для идеального газа, т.к. величины 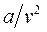(по сравнению с 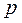) и 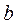(по сравнению с 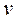) становятся пренебрежимо малыми.