1.12.1 Адиабатный процесс – процесс, происходящий без теплообмена с окружающей средой, т.е.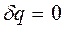 
. Для осуществления такого процесса следует:
1) теплоизолировать газ, поместив его в адиабатную оболочку;
2) провести процесс так быстро, чтобы изменение температуры газа из-за теплообмена с окружающей средой было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа. Это возможно, т.к. теплообмен протекает значительно медленнее, чем сжатие или расширение газа.
Уравнение адиабаты идеального газа при постоянном отношении теплоёмкостей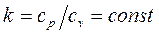 
:
; 
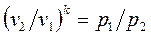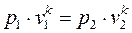. (1.65)
Величина
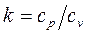(1.66)
называется показателем адиабаты. Подставив уравнение Майера в выражение (1.66), получим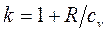 
. Поскольку видно, что 
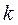>1, то в координатах 
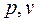(рисунок 7) линия адиабаты идёт круче линии изотермы: при адиабатном расширении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа.
Уравнение адиабатного процесса в форме, выражающей зависимость температуры от объёма или давления:
; 
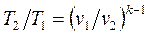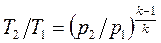. (1.67)
Работа расширения при адиабатном процессе согласно первому закону термодинамики совершается за счет уменьшения внутренней энергии и может быть вычислена по одной из формул:
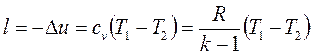, (1.68)
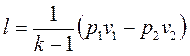, (1.69)
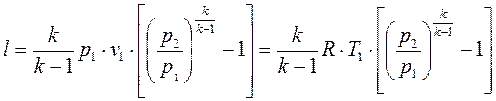. (1.70)
В данном процессе теплообмен газа с окружающей средой исключается, поэтому 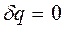. Выражение 
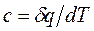показывает, что теплоёмкость адиабатного процесса равна нулю.
Т.к. при адиабатном процессе 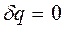, энтропия рабочего тела не изменяется ( 
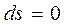и 
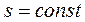). Следовательно, на 
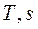- диаграмме адиабатный процесс изображается вертикалью (рисунок 7).
1.12.2 Политропный процесс – это процесс, удовлетворяющий уравнению
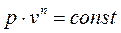. (1.71)
Подбирая соответствующее значение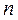 
, можно описать этим уравнением любой произвольный процесс в координатах 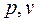. Показатель политропы 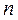может принимать любое численное значение в пределах от -∞ до +∞, но для данного процесса он является величиной постоянной.
Аналогично адиабатному процессу существуют выражения, устанавливающие связь между 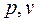и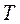 
в любых двух точках на политропе:
; 
; 
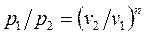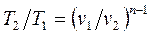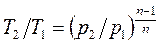(1.72)
Работа расширения в политропном процессе:
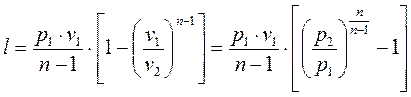, (1.73)
Уравнение (1.80) можно преобразовать к виду:
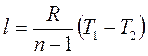, (1.74)
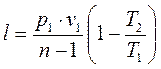, (1.75)
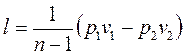, (1.76)
Количество подведенной (или отведенной) в процессе теплоты можно определить с помощью уравнения первого закона термодинамики: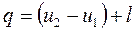 
.
Так как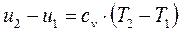 
; 
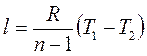, то
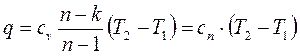, (1.77)
где
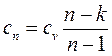(1.78)
представляет собой теплоёмкость идеального газа в политропном процессе. При постоянных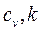 
и 
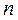теплоёмкость 
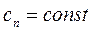, поэтому политропный процесс иногда определяют как процесс с постоянной теплоёмкостью.
Изменение энтропии в политропном процессе выражается формулой
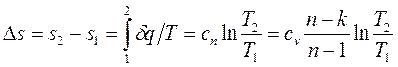, (1.79)
Политропный процесс имеет обобщающее значение, так как охватывает всю совокупность основных термодинамических процессов:
| Процесс |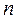 
| 
|
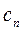
| Изохорный | +∞ |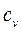 
|
| Изобарный | 0 |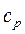 
|
| Изотермический | 1 | ∞ |
| Адиабатный |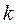 
| 0 |
На рисунке 8 показано взаимное расположение на 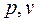и 
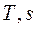- диаграммах политропных процессов с разными значениями показателя политропы. Все процессы начинаются в одной точке («в центре»).
Изохора (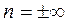 
) делит поле диаграммы на две области: процессы, находящиеся правее изохоры, характеризуются положительной работой, т.к. сопровождаются расширением рабочего тела; для процессов левее изохоры – работа отрицательна.
Процессы, расположенные правее и выше адиабаты, идут с подводом теплоты к рабочему телу; процессы, лежащие левее и ниже адиабаты, протекают с отводом теплоты.
Для процессов, расположенных над изотермой (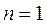 
), характерно увеличение внутренней энергии газа; процессы, расположенные под изотермой, сопровождаются уменьшением внутренней энергии.
Процессы, расположенные между адиабатой и изотермой, имеют отрицательную теплоёмкость, так как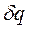 
и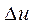 
(а следовательно, и 
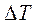, имеют в этой области противоположные знаки. В таких процессах 
> 
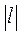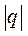, поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела.
1.13 Процесс парообразования. Основные понятия и определения
В качестве реального газа рассмотрим водяной пар – основное рабочее тело в теплоэнергетике. Изобразим процесс парообразования, т.е. превращения вещества из жидкого состояния в газообразное в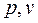 
- диаграмме (рисунок 9).
Начальное состояние воды с давлением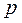 
и температурой 0°С на диаграмме изобразится точкой 
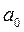. При подводе теплоты к воде при постоянном давлении её температура постепенно повышается до температуры кипения 
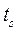, соответствующей данному давлению. Состояние жидкости, доведённой до температуры кипения, изображается на диаграмме точкой 
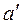. При дальнейшем подводе теплоты начинается кипение воды с сильным увеличением объёма. В этом случае вода – смесь жидкости и пара, которая называется влажным насыщенным паром (это двухфазная смесь, состоящая из пара со взвешенными в нём капельками жидкости). По мере подвода теплоты количество жидкой фазы уменьшается, а паровой – растёт. Температура смеси при этом остается неизменной и равной 
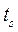, так как вся теплота расходуется на испарение жидкости. Когда последняя капля жидкости превращается в пар, то пар становится сухим насыщенным. Его состояние изображается точкой 
.
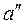Насыщенным называется пар, находящийся в термическом и динамическом равновесии с жидкостью, из которой он образуется.
Сухой насыщенный пар – это насыщенный пар, в котором отсутствуют частицы жидкой фазы. Его удельный объём и температура являются функциями давления, поэтому состояние сухого пара можно задать любым из параметров – давлением, удельным объёмом или температурой.
Степень сухости – массовая доля сухого насыщенного пара во влажном, обозначается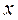 
.
Степень влажности – массовая доля кипящей воды во влажном паре, обозначается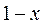 
. Для кипящей жидкости 
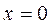, а для сухого насыщенного пара 
.
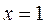Состояние влажного пара характеризуется двумя параметрами: давлением (или температурой насыщения 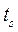, определяющей это давление) и степенью сухости пара.
При сообщении сухому пару теплоты при том же давлении его температура будет увеличиваться, пар будет перегреваться. Точка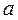 
изображает состояние перегретого пара и в зависимости от температуры пара может лежать на разных расстояниях от точки .
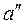Перегретым называется пар, температура которого превышает температуру насыщенного пара того же давления. Состояние перегретого пара определяется двумя любыми независимыми параметрами.
Если парообразование производить при более высоком давлении, то:
1) точка 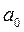остается на той же вертикали, т.к. вода практически несжимаема;
2) точка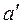 
смещается вправо из-за расширения жидкости с увеличением температуры кипения из-за роста давления;
3) точка 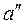смещается влево из-за падения удельного объёма под влиянием растущего давления.
Критическая точка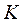 
– это точка, в которой удельные объёмы жидкости и пара сравниваются, а различия между жидкостью и паром исчезают. Для воды параметры критической точки составляют 
; 
; 
.
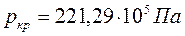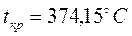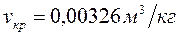Критическая температура – это максимально возможная температура сосуществования двух фаз; при больших температурах возможна только одна фаза.
Тройная точка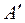 
- единственное состояние, в котором одновременно находятся в равновесии пар, вода и лёд. Параметры тройной точки для воды: 
; 
; 
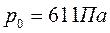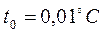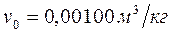. Изобара 
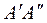при абсолютном давлении 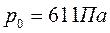- самая низкая для парообразования из воды. При более низких давлениях пар существует в равновесии только со льдом.
Сублимация – процесс образования пара непосредственно изо льда.
Линия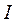 
- нулевая изотерма, каждая точка которой соответствует состоянию 1 кг воды при 0°С и давлении 
.
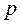Линия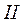 
- нижняя пограничная кривая, представляющая зависимость удельного объёма жидкости от давления при температуре кипения (состояние кипящей воды).
Линия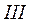 
- верхняя пограничная кривая, представляющая зависимость удельного объёма сухого насыщенного пара от давления (состояние сухого насыщенного пара).
Влево от линии 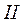до нулевой изотермы – область некипящей однофазной жидкости, вправо от кривой 
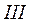- область перегретого пара. таким образом, кривые 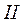и 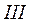ограничивают область насыщенного пара, отделяя её от области воды и перегретого пара (поэтому пограничные).
1.14 Параметры воды и пара. Теплота парообразования. Влажный пар
Термодинамические параметры кипящей воды и сухого насыщенного пара размещены в таблицах теплофизических свойств воды и водяного пара. В них термодинамические величины со штрихом относятся к воде, нагретой до температуры кипения, а величины с двумя штрихами – к сухому насыщенному пару.
Теплота парообразования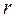 
– количество теплоты, необходимое для превращения одного килограмма воды в сухой насыщенный пар той же температуры. Из рисунка 9 находим :
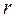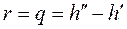. (1.87)
Приращение энтропии в процессе парообразования:
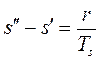. (1.88)
Так как состояние кипящей воды и сухого насыщенного пара определяется только одним параметром, то по известному давлению или температуре из таблиц воды и водяного пара берутся значения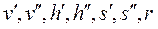 
.
Удельный объём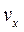 
, энтропия 
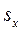и энтальпия 
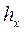влажного насыщенного пара определяются по правилу аддитивности. Так как в 1 кг влажного пара содержится 
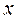кг сухого и 
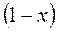кг кипящей воды, то
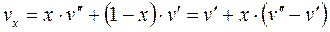; (1.89)
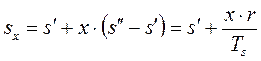; (1.90)
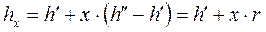. (1.91)
Непосредственно из таблиц параметры влажного пара взять нельзя. Их определяют по формулам (1.89) – (1.91) по заданному давлению (или температуре) и степени сухости.
По заданным давлению и температуре из таблиц находят требуемые параметры для воды и перегретого пара.
1.15 Вода и водяной пар. 
- и 
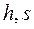- диаграммы. Основные термодинамические процессы
Для исследования различных процессов с водяным паром кроме таблиц используется 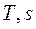- диаграмма. Она строится путем переноса числовых данных таблиц водяного пара в 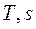- координаты (рисунок 10).
Состояние воды в тройной точке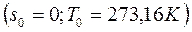 
изображается в диаграмме точкой 
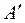. Откладывая для различных температур значения 
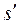и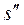 
, получим нижнюю и верхнюю пограничные кривые. Влево от нижней пограничной кривой располагается область жидкости, между пограничными кривыми – двухфазная область влажного насыщенного пара, вправо и вверх от верхней пограничной кривой – область перегретого пара.
На диаграмму наносят изобары, изохоры и линии постоянной степени сухости, для чего каждую изобару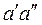 
делят на одинаковое число частей и соединяют соответствующие точки линиями 
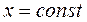. Область диаграммы, лежащая ниже нулевой изотермы, отвечает различным состояниям смеси пар + лёд.
На рисунке 11 показана 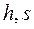- диаграмма для водяного пара, которая строится путём переноса числовых данных таблиц водяного пара в 
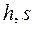- координаты. Построение аналогично 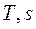- диаграмме.
Особенности 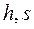- диаграммы:
1) изобары в двухфазной области влажного пара – это пучок расходящихся прямых;
2) в области насыщения изобара совпадает с изотермой;
3) чем больше давление, тем выше лежит изобара;
4) критическая точка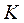 
лежит не на вершине, как в других диаграммах, а на левом склоне пограничной кривой;
5) в области перегрева изобары и изотермы расходятся: температура пара растёт по логарифмической кривой, а крутизна изобары увеличивается;
6) в области воды изобары имеют тот же характер, но проходят очень близко от пограничной кривой, практически сливаясь с ней;
7) при низких давлениях и высоких температурах пар по свойствам близок к идеальному газу, для которого при изотермическом процессе энтальпия постоянна, поэтому в диаграмме изотерма горизонтальна;
8) линии изохор идут круче изобар.
9) количество теплоты в изобарном процессе равно разности ординат конечной и начальной точек процесса и изображаются отрезком вертикальной прямой, а не площадью как в 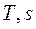- диаграмме.
Всю диаграмму не выполняют, а строят только её верхнюю часть, наиболее употребляемую для расчетов.
Общий метод расчета по 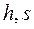- диаграмме состоит в следующем. По известным параметрам наносится начальное состояние рабочего тела, затем проводится линия процесса, и определяются его параметры в конечном состоянии. Далее вычисляется изменение внутренней энергии, определяются количества теплоты и работы в заданном процессе.
Изохорный процесс (рисунок 12):
1) изменение внутренней энергии
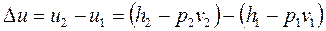. (1.92)
Данная формула справедлива для всех остальных термодинамических процесса.
2) работа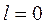 
;
3) теплота (из первого закона термодинамики) расходуется на увеличение внутренней энергии
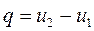. (1.93)
Изобарный процесс (рисунок 13):
1) изменение внутренней энергии – по уравнению (1.92);
2) теплота, полученная в процессе, равна разности энтальпий
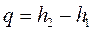. (1.94)
3) работа процесса
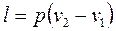. (1.95)
Изотермический процесс (рисунок 14):
1) внутренняя энергия водяного пара не остаётся постоянной (как у идеального газа), так как изменяется её потенциальная составляющая. Величина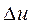 
находится по формуле (1.92);
2) количество полученной теплоты
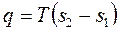. (1.96)
3) работа расширения определяется из первого закона термодинамики
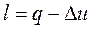. (1.97)
Адиабатный процесс (рисунок 15):
1) изменение внутренней энергии – по уравнению (1.92);
2) теплота не подводится;
3) работа адиабатного процесса
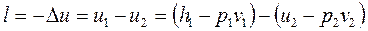. (1.98)
Дата: 2019-02-19, просмотров: 289.
