1.9.1 Энтропия – функция состояния системы, для которой выражение 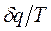 при равновесном изменении состояния газа есть полный дифференциал, обозначается для 1 кг газа через  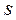и измеряется в 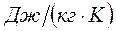. Для произвольного количества газа энтропия, обозначаемая через 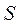, равна  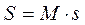и измеряется в Дж/К.

Аналитически энтропия определяется:

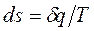                                                  .                                       (1.37)

Формула (1.37) справедлива для идеальных и реальных газов.

Подобно другим функциям состояния энтропия может быть представлена в виде функции любых двух параметров состояния:

.

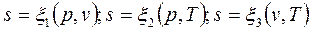Значение энтропии для заданного состояния определяется интегрированием уравнения (1.37):

,

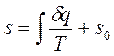где 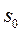 - константа интегрирования.

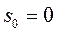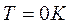При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. Нернст В. и Планк М. вывели следующий принцип: при температуре, стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю, т.е.  при  Это – третий закон термодинамики или тепловая теорема Нернста. Этот закон позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от произвольного уровня.

В технической термодинамике обычно используют не абсолютное значение энтропии, а её изменение в каком-либо процессе, поэтому энтропию тоже часто отсчитывают от произвольно выбранного уровня.

Изменение энтропии идеального газа можно вычислить по формулам:

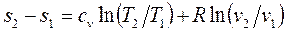                              ,                  (1.38)

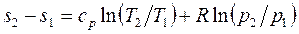                                  ,                (1.39)

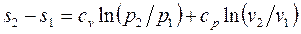                                  ,                (1.40)

Так как энтропия есть функция состояния рабочего тела, уравнениями (1.38) – (1.40) можно пользоваться независимо от пути перехода рабочего тела из начального в конечное состояние, а также от того, равновесный этот переход или нет.

1.9.2 Понятие энтропии позволяет ввести очень удобную для термодинамических расчетов  - диаграмму, на которой (как и на  - диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией.

Преобразовав выражение (1.37), получим

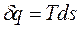                                                       ;                                    (1.41)

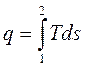                                                        .                                  (1.42)

В 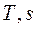 - диаграмме (рисунок 3) элементарная теплота процесса  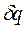изображается элементарной площадкой с высотой  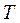и основанием 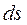, а площадь, ограниченная линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.

Формула (1.41) показывает, что 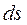 и 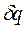 имеют одинаковые знаки, следовательно, по характеру изменения энтропии в равновесном процессе можно судить о том, в каком направлении происходит теплообмен: а) при нагревании тела ( 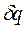>0) его энтропия возрастает ( 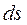>0); б) при охлаждении тела ( 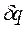<0) его энтропия убывает ( 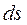<0).

1.9.3 Одним из важнейших понятий термодинамики является понятие об обратимых и необратимых процессах.

Термодинамический процесс представляет собой совокупность непрерывно изменяющихся состояний термодинамической системы. Между двумя состояниями 1и 2 системы можно представить себе два процесса, проходящих по одному и тому же пути: от состояния 1 к состоянию 2 и, наоборот, от состояния 2 к состоянию 1, так называемые прямой и обратный процессы.

Обратимыми называют процессы, в результате которых в прямом и обратном направлениях термодинамическая система возвращается в исходной состояние; таким образом совокупность прямого и обратного процессов не вызывает в окружающей среде никаких изменений.

Необратимыми называют процессы, при проведении которых в прямом и затем в обратном направлении система не возвращается в исходное состояние. В ходе процесса в системе происходят изменения, которые отличают её состояние после проведения обратного процесса от состояния, в котором она находилась до проведения прямого процесса.

Для обратимых процессов справедливо соотношение 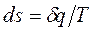. В необратимых процессах 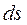> 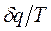, если под  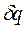понимать количество подведенной к системе или отведённой от неё теплоты.

Аналитические формулировки второго закона термодинамики:

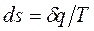- в обратимых процессах

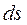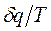> - в необратимых процессах.

Для теплоизолированных систем, которые не обмениваются теплотой с окружающей средой 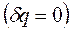, эти выражения приобретают вид:

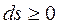                                                     .                                          (1.43)