Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Последовательность заполнения электронами уровней, подуровней, орбиталей в многоэлектронных атомах определяют:

- принцип наименьшей энергии;

- правило Клечковского;

- принцип запрета Паули;

- правило Гунда.   

1. Принцип наименьшей энергии: максимуму устойчивости системы соответствует минимум её энергии.

Следовательно, в соответствии с принципом наименьшей энергии, электроны будут вначале располагаться наатомных орбиталях, имеющих минимальную энергию, в этом случае связь электронов с ядром наиболее прочная и атомная система находится в состоянии максимальной устойчивости.

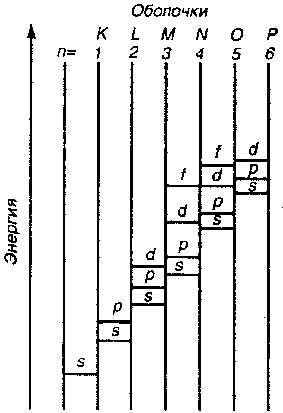
Рис. 2.4. Примерная схема относительного расположения энергетических подуровней в многоэлектронных атомах

В многоэлектронных атомах электроны испытывают не только притяжение ядер, но и отталкивание электронов, находящихся ближе к ядру и экранирующих ядро от более далеко расположенных электронов. Поэтому последовательность возрастания энергии орбиталей усложняется (см. рис. 2.4.).

2. Порядок возрастания энергии атомных орбиталей в сложных атомах описывается правилом Клечковского: при увеличении заряда ядра атома заполнение орбиталей происходит в порядке возрастания суммы главного и орбитального квантовых чисел (n+l), а при равных значениях суммы (n+l) – в порядке возрастания n.

Соответственно этому правилу, подуровни выстраиваются в следующий ряд: 1s<2s<2p<3s<3p<4s≈3d<4p<5s≈4d<5p<6s≈4f≈5d<6p<7s≈5f≈6d.

Например:

Подуровни	3d	4s	4p
n	3	4	4
l	2	0	1
n+l	5	4	5

 

Таким образом, в данном случае порядок заполнения будет следующий: 4s, 3d, 4p.

Исключение составляют d- и f-элементы с полностью и наполовину заполненными подуровнями, у которых наблюдается так называемый «провал» (или «проскок») электронов, например: Cu, Ag, Cr, Mo, Pd, Pt (это явление будет рассмотрено позднее).

3. Принцип запрета Паули: в атоме не может быть двух электронов с одинаковым набором четырех квантовых чисел.

Согласно этому принципу, на одной орбитали, характеризуемой определенными значениями трех квантовых чисел n, l и m_l, могут находиться только два электрона, отличающихся значением спинового квантового числа m_s, а именно m_s=+ 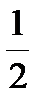 и m_s=– 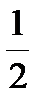, т.е. спины которых противоположно направлены.Символически это можно представить следующей схемой ..

Заполнение         и не допускается.

Принцип запрета Паули определяет электронную емкость энергетических уровней и подуровней:

- на s-подуровне (одна орбиталь) может быть два электрона,

- на p-подуровне (три орбитали) – шесть,

- на d-подуровне (пять орбиталей) – десять,

- на f-подуровне (семь орбиталей) – четырнадцать электронов.

Вобщем случае, максимальное число электронов на подуровне с орбитальным квантовым числом l равно 2(2l+1). Поскольку число орбиталей данного энергетического уровня равно n², емкость энергетического уровня составляет 2n² электронов, где n – соответствующее значение главного квантового числа.

4. Правило Гунда: устойчивому (невозбужденному) состоянию атома соответствует такое распределение электронов в пределах энергетического подуровня, при котором абсолютное значение суммарного спинового числа их (│∑m_s│) максимально.

Рассмотрим распределение электронов по энергетическим ячейкам в атоме углерода, электронная конфигурация которого 1s²2s²2p². Возможны три варианта:

а)                                  б)                                  в)

1s    2s   2p                       1s 2s   2p                       1s 2s  2p

∑m_s= 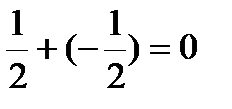            ∑m_s =+  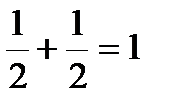           ∑m_s=0

Во всех вариантах спиновое число 1s²- и 2s²-электронов равно 0 (в каждой энергетической ячейке спины электронов антипараллельны).

Суммарное спиновое число p-электронов в вариантах a) и в) равно нулю (∑m_s=0), а в варианте (б) ∑m_s=1.

В соответствии с правилом Гунда реализуется только вариант (б).

Другими словами:заполнение орбиталей одного подуровня в основном состоянии атома начинается одиночными электронами с одинаковыми спинами. После того как одиночные электроны займут все орбитали в данном подуровне, заполняются орбитали вторыми электронами с противоположными спинами.