Поверхностное натяжение.

1. . Какую температуру Т имеет масса m=2г азота, занимающего объём V=820см² при давлении р=0,2МПа? Газ рассматривать как: а) идеальный; б) реальный.

2. В баллоне вместимостью V=8л находится кислород массой m=0,3кг при температуре Т=300К. Найти, какую часть вместимости сосуда составляет собственный объём молекул газа. Определить отношение внутреннего давления 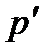 к давлению р газа на стенки сосуда.

3. Тонкое алюминиевое кольцо радиусом 8см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Масса кольца 7г. Температуру раствора считать комнатной.

4. Деревянная палочка длиной 4см плавает на поверхности воды. По одну сторону от палочки осторожно налили мыльный раствор. С каким ускорением начнет двигаться палочка, если ее масса 1г.? Сопротивление воды при движении палочки не учитывать.

5. Какая масса ртути содержится в единице объема воздуха зараженного ртутью помещения при температуре 20⁰С, если давление насыщенного пара ртути при этой температуре 0,15Па? Молярная масса ртути 200г/моль.

6. В отростке сосуда, закрытого поршнем, находится некоторая масса воды в равновесии с насыщенным паром. Диаметры сосуда и отростка 5см и 2мм. Поддерживаемая температура 20⁰С, поршень опускается на высоту 10см; уровень воды в отростке при этом повышается на высоту 1мм. Определите давление насыщенного пара воды при 20⁰С.

7. Термос заполнен кипящей водой и герметически закрыт крышкой. Какая сила потребуется (после охлаждения) для того, чтобы вытащить пробку диаметра 3см? Трением пренебречь. Давление пара над остывшей водой мало.

8. Смешали 1м³ воздуха с относительной влажностью 20% и 2м³ воздуха с относительной влажностью 30%. При этом обе порции были взяты при одинаковой температуре. Смесь занимает 3м³. Определить ее относительную влажность.

9. Найти давление p воздуха в воздушном пузырьке диаметром d =0,01 мм, находящемся на глубине h = 20 см под поверхностью воды. Атмосферное давление p₀ = 101,7 кПа.

10. Диаметр d канала стеклянной трубки чашечного ртутного барометра равен 5 мм. Какую поправку ∆p нужно вводить в отсчеты по этому барометру, чтобы получить верное значение атмосферного давления?

11. На какую высоту h поднимается вода между двумя параллельными стеклянными пластинами, если расстояние d между ними равно 0,2 мм?

12. В дне сосуда с ртутью имеется отверстие. Каким может быть наибольший диаметр d отверстия, чтобы ртуть из сосуда не выливалась при высоте столба ртути h = 3 см?

Д.З.

1. В закрытом сосуде объемом V=0,5м³ находится количество ν=0,6кмоль углекислого газа при давлении p=3МПа. Пользуясь уравнением Ван-дер-Ваальса, найти, во сколько раз надо увеличить температуру газа, чтобы давление увеличилось вдвое.

2. Вычислите критическую температуру T_кр и давление p_кр: 1) кислорода; 2) воды.

3. Какая энергия освобождается при слиянии мелких водяных капель радиусом 0,002мм в одну каплю радиусом 2мм.

4. Разность уровней смачивающей жидкости в коленах U-образной трубки 23мм. Диаметр каналов в коленах трубки 2 и 0,4мм. Плотность жидкости 800кг/м³. Определите поверхностное натяжение жидкости.

5. В цилиндре под поршнем сечением 100см² находится 18г воды при температуре 0⁰С. Цилиндр нагревается до температуры 200⁰С. На какую высоту поднимется поршень с лежащим на ней грузом массой 100кг? Атмосферное давление 10⁵Па. Давление насыщенного пара при температуре 200⁰С – 1,6МПа.

6. .В вертикально расположенном цилиндре под поршнем массы 10кг находится некоторое количество воздуха, воды и водяного пара при температуре 100⁰С. В положении равновесия поршень отстоит от дна цилиндра на расстояние 20см. Когда цилиндр расположили горизонтально, поршень занял новое положение равновесия, переместившись на расстояние 3см от первоначального положения. Какая масса воды была на дне сосуда? Площадь поршня 400см².

7. В капиллярной трубке радиусом 0,5 мм жидкость поднялась на 11 мм. Найти плотность данной жидкости, если ее коэффициент поверхностного натяжения 22 мН/м.

8. На какой глубине h под водой находится пузырек воздуха, если известно, что плотность воздуха в нем ρ=2 кг/м³? Диаметр пузырька d=15 мкм, температура t=20°С, атмосферное давление p₀=101.3 кПа.

9. Из вертикальной трубки внутренним радиусом r = 1,5 мм вытекает керосин. Найти радиус R капли в момент отрыва. Каплю считать сферической. Диаметр шейки капли в момент отрыва считать равным внутреннему диаметру трубки.

Семинар 12.

Гидродинамика.

Уравнение неразрывности струи

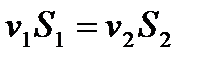,где S ₁ и S ₂ – площади поперечного сечения трубки тока в двух местах; v₁ и v₂  –соответствующие скорости течений.

· Уравнение Бернулли для идеальной несжимаемой жидкости в общем случае

,

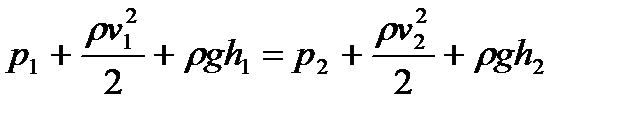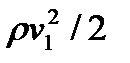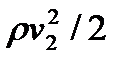где p ₁ и р₂ – статические давления жидкости в двух сечениях трубки тока; v₁ и v_{2 –}скорости жидкости в этих сечениях;  и  – динамические давления жидкости в этих же сечениях; h ₁ и h ₂ – высоты их над некоторым уровнем (рис. 12.1); pgh ₁ и pgh ₂ – гидростатические давления.

Уравнение Бернулли в случае, когда оба сечения находятся на одной высоте ( h ₁ = h ₂ )

.

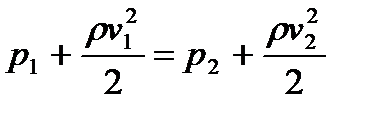· Скорость течения жидкости из малого отверстия в открытом широком сосуде

,

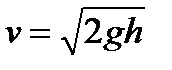где h — глубина, на которой находится отверстие относительно уровня жидкости в сосуде.

· Формула Пуазейля. Объем жидкости (газа), протекающей за время t через длинную трубку,

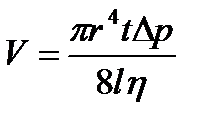
где r — радиус трубки; l – ее длина; Δp – разность давлений на концах трубки; η – динамическая вязкость (коэффициент внутреннего трения) жидкости.

· Число Рейнольдса для потока жидкости в длинных трубках

,

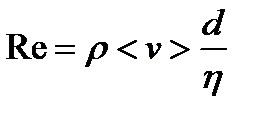где <v> – средняя по сечению скорость течения жидкости; d – диаметр трубки, и для движения шарика d жидкости

,

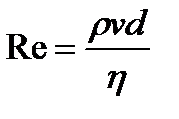где v – скорость шарика; d—его диаметр.

Число Рейнольдса Re есть функция скорости v тела, линейной величины l, определяющей размеры тела, плотности р и динамической вязкости η жидкости, т. е.

.

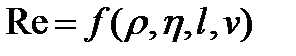При малых значениях чисел Рейнольдса, меньших некоторого критического значения Re_кp, движение жидкости является ламинарным. При значениях Re>>Re_кр движение жидкости переходит в турбулентное.

Критическое число Рейнольдса для движения шарика в жидкости Re_кр=0,5; для потока жидкости в длинных трубках Re_кр=2300.

· Формула Стокса. Сила сопротивления F , действующая со стороны потока жидкости на медленно движущийся в ней шарик,

,

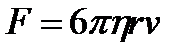где r – радиус шарика; v – его скорость.

Формула справедлива для скоростей, при которых число Рейнольдса много меньше единицы (Re<<l).

Гидродинамика.

1. Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м³.

2. Два тела плотностью ρ₁ и ρ₂ в пустоте имеют один и тот же вес. Их подвешивают к концам рычага и помещают в жидкость плотностью ρ. Каково должно быть отношение плеч рычага, чтобы не нарушилось равновесие?

3. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S₁, сечение струи S₂. Найдите ускорение, с которым перемещается уровень воды в сосуде.

4. 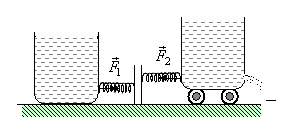В сосуде с жидкостью сделано отверстие площадью S. Размеры отверстия малы по сравнению с высотой столба жидкости. В одном случае отверстие закрыто пластинкой и измеряется сила давления жидкости на пластинку F1 при высоте столба жидкости h (рис.). В другом случае тот же сосуд стоит на тележке, отверстие открыто, и измеряется сила отдачи F2 при установившемся токе жидкости в момент, когда высота столба жидкости будет та же, что и в первом случае. Будут ли силы F₁ и F₂ равны?

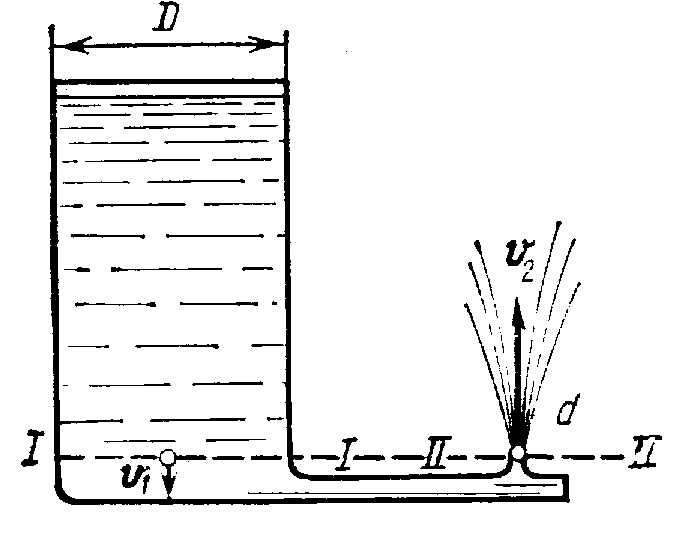
5. Из отверстия II—II в цилиндрическом бака бьет вода со скоростью v₂ =12 м/с. Диаметр D бака равен 2 м, диаметр d сечения II—II равен 2 см. Найти: 1) скорость v₁ понижения воды в баке; 2) давление p ₁ , под которым вода подается в фонтан; 3) высоту h ₁ уровня воды в баке и высоту h ₂ струи, выходящей из фонтана.

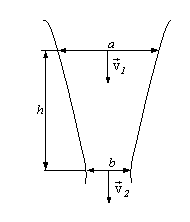
6. Из крана выливается вода. Начиная с некоторого места, диаметр струи уменьшается на протяжении h от а до b (рис. ). Сколько воды вытечет из крана за время t?

7. Площадь поршня в шприце S₁ = 2 см², а площадь отверстия S₂ = 1 мм² (рис. 4). Сколько времени будет вытекать вода из шприца, если действовать на поршень с силой F = 5 H и если ход поршня l = 5 см?

8. В сосуде с глицерином падает свинцовый шарик. Определить максимальное значение диаметра шарика, при котором движение слоев глицерина, вызванное падением шарика, является еще ламинарным. Движение считать установившимся.