1. Зная функцию распределения молекул по скоростям, вывести формулу наиболее вероятной скорости Jв.
2. Преобразовать функцию распределения Максвелла, перейди от переменной v к переменной 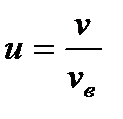 , где vв – наиболее вероятная скорость молекул.
, где vв – наиболее вероятная скорость молекул.
3. Какова вероятность того, что данная молекула идеального газа имеет скорость, отличную от ½Jв не более чем на 1 %?
4. В сосуде находится газ, количество вещества которого равно1,2 моль. Рассматривая этот газ, как идеальный определите число молекул  N, скорость которых меньше 0,001 наиболее вероятной скорости молекул.
N, скорость которых меньше 0,001 наиболее вероятной скорости молекул.
5. Определить, какая из двух средних величин, <1/J> или 1/<J>, больше, и найти их отношение.
6. Водород находится при нормальных условиях и занимает объем V=1 см3. Определить число N молекул в этом объеме, обладающих скоростями, меньшими некоторого значения Jmax=1 м/с.
7. По функции распределения молекул по скоростям определить среднее значение квадрата скорости.
8. При какой температуре число молекул азота 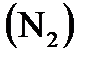 , обладающих скоростями в интервале от 299 до 301 м/с, равно числу молекул, обладающих скоростями в интервале от 599 до 601 м/с?
, обладающих скоростями в интервале от 299 до 301 м/с, равно числу молекул, обладающих скоростями в интервале от 599 до 601 м/с?
9. В сосуде находится 8,00 г кислорода 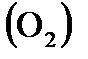 при температуре 1600К. Какое число молекул кислорода
при температуре 1600К. Какое число молекул кислорода 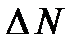 имеет скорость поступательного движения, превышающую скорость звука в воздухе 340м/с?
имеет скорость поступательного движения, превышающую скорость звука в воздухе 340м/с?
Д.З.
1. Какая часть молекул кислорода при t=0°С обладает скоростями v от 100 до 110 м/с?
2. Найти относительное число молекул ΔN/N гелия, скорости которых отличаются от наиболее вероятной - не более чем на 10 м/с, при температуре газа T=300 К.
3. Вычислить среднюю скорость < vкв > молекул кислорода при температуре Т = 300 К. Найти относительное число молекул, скорости которых отличаются от средней квадратичной скорости не более чем на 1%.
4. Найти выражение средней кинетической энергии <E> поступательного движения молекул. Функцию распределения молекул по энергиям считать известной.
5. По функции распределения молекул по скоростям определить среднюю квадратичную скорость < vкв >.
6. Используя функцию распределения молекул по энергиям, определить наиболее вероятное значение энергии Ев.
7. Вывести формулу наиболее вероятного импульса pв молекул идеального газа.
8. Вывести формулу, определяющую среднее значение компонента импульса <px> молекул идеального газа.
9. Преобразовать функцию f(E)dE распределения молекул по кинетическим энергиям в функцию f(Θ)dΘ распределения молекул по относительным кинетическим энергиям (где 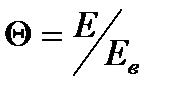 ; Eв - наиболее вероятное значение кинетической энергии молекул).
; Eв - наиболее вероятное значение кинетической энергии молекул).
Семинар 6.
Дата: 2019-02-25, просмотров: 414.