Обзор суммативного оценивания за 2 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий
МВО – задания с множественным выбором ответов
КО – задания, требующие краткого ответа
РО – задания, требующие развернутого ответа.
Структура суммативной работы
Данный вариант состоит из 7 заданий, включающих вопросы с множественным выбором ответов, с кратким и развернутым ответом.
В вопросах с множественным выбором ответов учащийся выбирает правильный ответ из предложенных вариантов ответов.
В вопросах, требующих краткого ответа, учащийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, учащийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность учащегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания за 2 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задания * | Время на выполнение, мин* | Балл* | Балл за раздел |
|
Функция. График функции | 7.4.1.5 знать определение линейной функции 𝑥𝑥 = 𝑘𝑥𝑥 + 𝑏, строить её график и устанавливать его расположение в зависимости от значений k и b | Применение |
1 |
1 |
МВО |
2 |
1 |
12 |
| 7.4.1.7 определять знаки k и b линейной функции 𝑥𝑥 = 𝑘𝑥𝑥 + 𝑏, заданной графиком | Применение | |||||||
| 7.4.1.12 строить график функции у = к (𝑘 ≠ 0) и знать её свойства х | Применение | 1 | 2 | МВО | 2 | 1 | ||
| 7.4.1.9 задавать формулой линейную функцию, график которой параллелен графику данной функции или пересекает его | Применение |
1 |
3 |
КО |
6 |
3 | ||
| 7.4.1.4 знать определение функции 𝑥𝑥 = 𝑘𝑥𝑥, строить её график и устанавливать его расположение в зависимости от k | Применение | |||||||
| 7.4.2.4 решать системы линейных уравнений графическим способом | Применение | 1 | 5 | РО | 6 | 3 | ||
| 7.4.1.6 находить точки пересечения графика линейной функции с осями координат (без построения графика) | Применение |
1 |
7 |
РО |
8 |
4 | ||
| 7.4.1.5 знать определение линейной функции 𝑥𝑥 = 𝑘𝑥𝑥 + 𝑏, строить её график и устанавливать его расположение в зависимости от значений k и b | Применение | |||||||
| 7.4.1.8 обосновывать взаимное расположение графиков линейных функций в зависимости от значений их коэффициентов | Навыки высокого порядка |
|
Элементы статистики | 7.3.3.2 вычислять абсолютную и относительную частоты варианты | Применение |
1 |
4 |
РО |
8 |
4 |
8 |
| 7.3.3.5 проверять данные таблицы на непротиворечивость | Применение | |||||||
| 7.3.3.7 анализировать статистическую информацию, представленную в виде таблицы или полигона частот | Навыки высокого порядка | 1 | 6 | КО | 8 | 4 | ||
| ИТОГО: | 7 | 40 минут | 20 | 20 | ||||
| Примечание: * - разделы, в которые можно вносить изменения | ||||||||
Образец заданий и схема выставления баллов
Задания суммативного оценивания за 2 четверть по предмету «Алгебра»
1. Найдите значение коэффициента k, если известно, что график функции через точку с координатами А (1; –3).
y = k проходит
x
A) 3
B) 1
C) -1
D) -3
2. Найдите координаты точки пересечения функции A) (-16;0)
æ 1 ; 0ö
y = - 3 x - 12 с осью абсцисс:
4
[1]
|
|
|
|
 |
C) ç 16 ÷
D) (16;0)
[1]
3. Задайте формулой функцию, график которой проходит через точку (0; 4) и параллелен графику функции y = –3x.
[3]
4. Социологи опросили 20 школьников, выясняя, сколько книг каждый из них прочел за прошедший месяц. Были получены следующие данные:
3, 0, 1, 5, 1, 2, 3, 3, 1, 1, 3, 0, 3, 4, 2, 4, 5, 5, 6, 2
a) постройте таблицу абсолютных частот и таблицу относительных частот;
b) укажите самое распространенное число прочитанных книг;
c) проверьте таблицу относительных частот на непротиворечивость.
[4]
5. Решите графическим методом систему уравнений:
ì y + 0,5x = 2
|
[3]
6. Результаты письменного экзамена по математике (максимальный балл – 10) представлены полигоном абсолютных частот. Проанализируйте информацию и найдите:
a)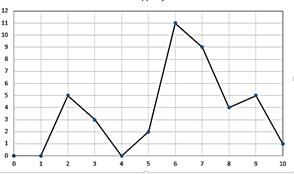 
объем выборки;
b) балл, полученный большим количеством учеников
c) процент учащихся, имеющих высокий результат, если считать, что 8,9,10 баллов – это высокий результат,
7. График функции, заданной уравнением с координатами (-2;0).
a) найдите значение а ;
[4]
y = (a + 1)x + a - 1 пересекает ось абсцисс в точке
b) запишите функцию в виде
y = kx + b ;
c) не выполняя построения графика функции, определите, через какую четверть график не
проходит.
[4]
Схема выставления баллов
| № | ||||||||||||||||||
Ответ
D
А
3
y=-3x+b
b=4
y=-3x+4
4
1
0
1
3
5
6
2
4
5
3
1
1
Принимать любой альтернативный вариант
0
1
2
3
4
5
6
Относительн ая частота
4
20
2
20
3
1
20
20
или
|
|
|
% |
| ||||||||
|
| Числок ниг | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |||
| Относи тельная частота | 10 % | 20 % | 15 % | 25 % | 10 % | 15 % | 5 | ||||
| Самое распространённое – 3. | 1 | ||||||||||
| 2 + 4 + 3 + 5 + 2 + 3 + 1 =1 20 20 20 20 20 20 20 или 10%+20%+15%+25%+10%+15%+5%=100% | 1 | ||||||||||
|
5 | Изображает график функции y = -0,5x + 2 | 1 | |||||||||
| Изображает график функции y = 2x - 3 | 1 | ||||||||||
| Находит координаты точки пересечения графиков : x=2, y=1 | 1 | (2;1) | |||||||||
|
6 | 40 | 1 | |||||||||
| 6 | 1 | ||||||||||
| 10 ×100% / 1 ×100 / 4 + 5 +1 ×100% 40 4 40 | 1 | ||||||||||
| 25% | 1 | ||||||||||
|
7 | Для нахождения значения а, в заданное уранение подставляет координаты точки, через которую проходит график функции | 1 | |||||||||
| a) a=-3 | 1 | ||||||||||
| b) y = -2x - 4 | 1 | ||||||||||
| c) I четверть | 1 | ||||||||||
|
Всего баллов | 20 | ||||||||||
Дата: 2019-02-25, просмотров: 553.
