Система состоит из n элементов. Пусть d _j – затраты на один элемент j-го типа, P _j − вероятность отказа элемента j-го типа, С – суммарные затраты на все элементы. Определить число элементов j-го типа, 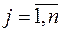, которые нужно держать в резерве, чтобы максимизировать показатель надежности системы при заданных ограничениях на затраты.

Задача компоновки модулей

При проектировании цифровой аппаратуры

Проектируемое устройство состоит из m различных модулей 2-го уровня, модули 2-го уровня компонуются из n различных модулей 1-го уровня. Пусть 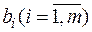 – минимальное число модулей i-го типа 2-го уровня, требуемых для компоновки схемы,  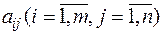– число модулей j-го типа 1-го уровня, из которых можно скомпоновать один модуль i-го типа 2-го уровня, C _j – стоимость одного модуля j-го типа 1-го уровня. Задача состоит в минимизации стоимости устройства.

19. Задача оптимизации плана производства

Фирма имеет три швейных цеха, где производятся костюмы трех видов. Затраты на производство костюмов различны, производственные мощности цехов ограничены. Цены реализации костюмов различны.

Составить оптимальный план производства, дающий максимальную прибыль.

Распределение заданий между швейными фабриками

Плановое задание по изготовлению 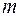 моделей костюмов необходимо распределить между n швейными фабриками. Производственные мощности i-й фабрики позволяют за рассматриваемый отрезок времени выпустить  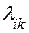костюмов k-й модели. Заданы цены  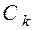на костюм k-й модели и себестоимости  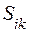изготовления k-й модели на i-й фабрике. Плановое задание k-й модели − .

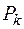1. Составить оптимальный план загрузки фабрик из условия максимизации прибыли.

2. Составить оптимальный план загрузки фабрик, обеспечивающих максимальное число комплектов костюмов, если числа планового задания рассматривать как ассортиментные отношения.

Производство оптимального набора продуктов

Фабрика может производить n различных продуктов, располагая для этого m видами ресурсов в количестве 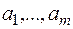. Для производства продуктов могут быть использованы S технологических способов. Заданы величины 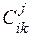, характеризующие нормы расхода i-го ресурса на единицу k-го продукта при изготовлении его j-м способом. Известна цена P _k единицы k-го продукта. Составить модель задачи по определению оптимального набора продуктов и способов их производства из условия максимизации товарной продукции при дополнительном условии, согласно которому любой k-й продует либо должен производиться в количестве, не меньшем d _k, либо совсем не производиться.