Задача оптимального резервирования
Система состоит из n элементов. Определить x j − число элементов j-го типа 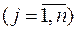 , минимизирующее суммарные затраты на резерв при заданном ограничении d на показатель надежности системы, если d j – затраты на один элемент j-го типа,
, минимизирующее суммарные затраты на резерв при заданном ограничении d на показатель надежности системы, если d j – затраты на один элемент j-го типа, 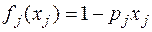 − значение показателя надежности по j‑му типу элемента (p j − вероятность отказа элемента j-го типа).
− значение показателя надежности по j‑му типу элемента (p j − вероятность отказа элемента j-го типа).
Оптимизация распределения машин по маршрутам
Имеется n маршрутов, по каждому из которых необходимо совершить 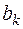 рейсов
рейсов 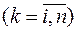 , и m автомашин (
, и m автомашин ( 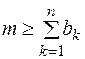 ), каждая из которых может быть использована в течение
), каждая из которых может быть использована в течение 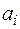 часов (
часов ( 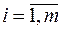 ). На выполнение i-й машиной рейса по k-му маршруту требуется
). На выполнение i-й машиной рейса по k-му маршруту требуется 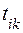 часов при затратах
часов при затратах 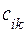 рублей.
рублей.
Составить модель задачи оптимального распределения машин по маршрутам.
Распределение памяти ЭВМ
Пусть имеются массивы информации n типов, di – объем массива i-го типа. Память j-го типа характеризуется быстродействием, ti – емкостью 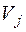 и стоимостью единицы памяти C j, общая стоимость памяти не должна превышать L.
и стоимостью единицы памяти C j, общая стоимость памяти не должна превышать L.
Распределить массивы информации по уровням памяти оптимально.
Задача оптимального выпуска продукции
Фирма имеет три цеха производства продукции четырех видов, затраты на производство различны, производственные мощности цехов ограничены.
Составить оптимальный план выпуска изделий с минимальными затратами.
Задача о размещении складов
Планируется построение складов известной емкости в различных местах. Затраты на построение склада данной емкости и в данном месте различны.
Выбрать такие места для расположения складов, чтобы выполнить заказ на суммарную емкость и чтобы суммарные затраты были минимальны.
Задача о производстве и распределении продукта
Фирма по заготовке сырья имеет три пункта, затраты на заготовку единицы сырья в различных пунктах различны. Мощности пунктов ограничены. Фирма имеет обязательства перед 5 пунктами потребления сырья по заданным партиям поставок.
Обеспечить потребителей сырьем с минимальными затратами на заготовку.
Задача о выборе производственной программы
Из ограниченных запасов сырья m видов производится продукция n видов. Известны расходы сырья на производство единицы продукции. Известна прибыль от единицы каждого изделия, выпущенного по плану, и прибыль от изделия, выпущенного сверх плана.
Найти план выпуска изделий с максимальной суммарной прибылью.
Распределение памяти ЭВМ
Рассматривается многоступенчатая система хранения данных: на верхнем уровне используются ЗУ большого объема, но с малым быстродействием, на нижнем уровне – ЗУ небольшого объема, но с большим быстродействием. Пусть m – число уровней памяти, n – число массивов информации, 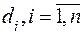 – объем i-го массива,
– объем i-го массива, 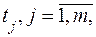 – быстродействие памяти j-го типа,
– быстродействие памяти j-го типа, 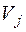 – объем памяти j-го типа.
– объем памяти j-го типа.
Распределить массивы информации по уровням памяти так, чтобы свести к минимуму время их обработки (суммарное время обращения к памяти).
Задача компоновки модулей
Оптимизация машинного парка
Имеются m типов машин в количествах d1,…, dm и видов работ, подлежащих выполнению в объёмах 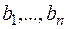 . Задана матрица
. Задана матрица 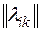 , где
, где 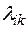 – производительность i-й машины на k-й работе, матрица
– производительность i-й машины на k-й работе, матрица 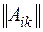 , где
, где 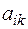 – себестоимость выполнения единицы k-й работы машиной i-го типа и стоимость
– себестоимость выполнения единицы k-й работы машиной i-го типа и стоимость 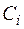 одной машины i-го типа.
одной машины i-го типа.
Составить математическую модель задачи по определению оптимального машинного парка (т.е. количество машин каждого типа) и оптимального его распределения по указанным работам из условия минимизации суммарной стоимости (машинного парка и произведенных работ).
27. Задача оптимального планирования
Имеется фирма в составе двух предприятий, производящих соответственно два и четыре различных вида продукции. Каждое предприятие для производства продукции использует свои внутренние, локальные ресурсы (рабочую силу и оборудование). Предприятия совместно потребляют некоторый лимитированный ресурс (сырьё). Пусть b − количество общего ресурса, b1, b2 – ресурсы первого предприятия, b3, b4 − ресурсы второго предприятия, a ij − количество i-го ресурса, необходимое для производства j-го вида продукции, С i − прибыль фирмы от реализации единицы i-й продукции.
Определить план производства продукции, дающий максимальную прибыль.
Задача загрузки станков
Ткацкая фабрика располагает N1 станками первого типа и 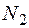 станками второго типа. Станки могут производить три вида тканей:
станками второго типа. Станки могут производить три вида тканей: 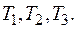 Каждый вид станка может производить любой из видов ткани, но в неодинаковом количестве. Станок первого типа производит в единицу времени
Каждый вид станка может производить любой из видов ткани, но в неодинаковом количестве. Станок первого типа производит в единицу времени 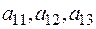 метров ткани
метров ткани 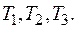 соответственно, станок второго типа
соответственно, станок второго типа 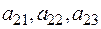 метров ткани. Каждый метр ткани
метров ткани. Каждый метр ткани 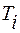 – приносит прибыль
– приносит прибыль 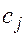 ,
, 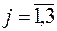 . Согласно плану производства фабрика должна произвести в единицу времени не менее
. Согласно плану производства фабрика должна произвести в единицу времени не менее 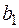 метров ткани
метров ткани 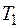 , не менее
, не менее 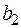 метров ткани
метров ткани 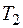 и не менее
и не менее 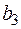 метров ткани
метров ткани 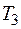 .
.
Требуется распределить загрузку станков производством тканей различного вида так, чтобы план был выполнен и при этом прибыль в единицу времени была максимальна.
Размещение производства
Имеются q пунктов потребления, потребности которых в некотором продукте измеряются величинами 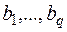 . Для удовлетворения этих потребностей могут быть использованы Р пунктов возможного производства продукта. Задана матрица
. Для удовлетворения этих потребностей могут быть использованы Р пунктов возможного производства продукта. Задана матрица 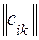 затрат на перевозки единицы продукта из i-го пункта производства в k-й пункт потребления. Предполагается, что в каждом i-м пункте возможны n i взаимоисключающих вариантов производства с объемами
затрат на перевозки единицы продукта из i-го пункта производства в k-й пункт потребления. Предполагается, что в каждом i-м пункте возможны n i взаимоисключающих вариантов производства с объемами 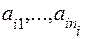
Определить оптимальный план размещения производства из условия минимизации затрат на транспортировку продукта.
Задача о выпуске продукции
Предприятие производит n видов продукции, спрос на которую является функцией времени 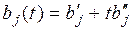 . Для изготовления продукции используются m видов сырья, запасы которого задаются вектором
. Для изготовления продукции используются m видов сырья, запасы которого задаются вектором 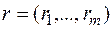 . Изготовление единицы продукции вида
. Изготовление единицы продукции вида 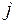 требует
требует 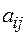 единиц сырья вида
единиц сырья вида 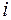 , а её стоимость равна
, а её стоимость равна 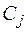 .
.
1. Определить оптимальные планы выпуска продукции.
2. Решить задачу при дополнительном условии, что вектор ресурсов r также меняется со временем, причем 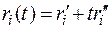 .
.
Вычислительного устройства
Устройство должно состоять из m блоков, вычисляющих последовательно определенные функции. Имеется 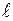 различных вариантов выполнения каждого блока, отличающихся схемным решением. Заданы ограничения в отношении максимальной стоимости
различных вариантов выполнения каждого блока, отличающихся схемным решением. Заданы ограничения в отношении максимальной стоимости 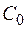 , максимальных габаритов
, максимальных габаритов 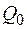 , максимального времени выполнения устройством всей совокупности функций
, максимального времени выполнения устройством всей совокупности функций 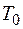 . Известны данные по стоимости
. Известны данные по стоимости 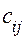 , габаритам
, габаритам 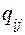 и времени вычисления функций
и времени вычисления функций 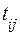 для каждого блока
для каждого блока 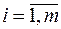 при каждом варианте его выполнения
при каждом варианте его выполнения 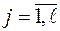 .
.
Сформулировать возможные варианты постановки задачи оптимального построения вычислительного устройства.
Приобретение товаров
Получатель имеет сумму денег J и может купить товары трёх видов по цене 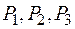 за единицу. Функция полезности товара для покупателя имеет вид
за единицу. Функция полезности товара для покупателя имеет вид 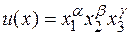 , где
, где 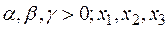 − количество товаров, которые он покупает.
− количество товаров, которые он покупает.
Определить, какое количество товара каждого вида выгодно приобрести покупателю.
Управление ресурсами
Имеется начальное количество ресурсов K, которое нужно распределить между N отраслями производства. Единица ресурсов, вложенных в i-ю отрасль, приносит доход 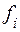 .
.
Требуется найти способ управления ресурсами, при котором суммарный доход будет максимальный.
Разбиение системы на блоки
АСУ состоит из N элементов. Число соединений между элементами, определяемое структурой АСУ, задается симметричной квадратной матрицей 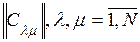 . Из условий эксплуатации системы следует, что целесообразно разбить АСУ на m блоков, в каждом из которых не более n элементов. При разбиении системы на блоки одни связи окажутся внутриблочными, другие – внешними.
. Из условий эксплуатации системы следует, что целесообразно разбить АСУ на m блоков, в каждом из которых не более n элементов. При разбиении системы на блоки одни связи окажутся внутриблочными, другие – внешними.
Задача: минимизировать число внешних соединений (или максимизировать число внутренних связей).
Задача о выборе поставщиков
Фирма по производству хлебобулочных изделий имеет трех поставщиков сырья. Закупочные цены на сырье различны, стоимость доставки единицы сырья различна. Фирма имеет обязательства перед поставщиками о минимальном закупочном сырье. Известны расходы сырья на единицу каждого изделия. Ассортимент состоит из 5 изделий. Производительные и финансовые возможности фирмы ограничены.
Программа обработки изделия
Найти оптимальную программу обработки 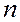 изделий на
изделий на 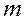 взаимозаменяемых станках при заданных исходных данных:
взаимозаменяемых станках при заданных исходных данных: 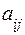 − норма времени для обработки одного j-го изделия на i-м станке;
− норма времени для обработки одного j-го изделия на i-м станке; 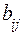 − себестоимость обработки, р/ч, одного j-го изделия на i-м станке;
− себестоимость обработки, р/ч, одного j-го изделия на i-м станке; 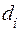 − общее время работы i-го станка;
− общее время работы i-го станка;
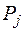 − план обработки изделий j-го типа;
− план обработки изделий j-го типа; 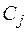 − прибыль, получаемая при реализации одного изделия j-го типа.
− прибыль, получаемая при реализации одного изделия j-го типа.
В качестве критерия оптимальности выбрать:
1) минимум себестоимости;
2) минимум затрат времени работы станков;
3) максимум прибыли.
Распределение ресурсов
Комплексная целевая программа включает К подпрограмм. Известно, что для выполнения i-й подпрограммы в полном объеме достаточно ресурсов в количестве 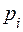 , степень же выполнения подпрограммы при выделении на неё
, степень же выполнения подпрограммы при выделении на неё 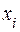 ресурсов составляет
ресурсов составляет 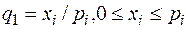 . Степень выполнения всей программы определяется как
. Степень выполнения всей программы определяется как 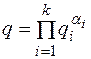 , где
, где 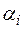 – коэффициент важности i-й подпрограммы.
– коэффициент важности i-й подпрограммы.
Найти оптимальное распределение общего ресурса объема S подпрограммам в случае дефицита 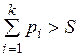 .
.
Задача выбора
Имеются 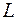 работ и
работ и 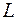 сотрудников, которые должны быть назначены на выполнение этих работ. Каждый j-й сотрудник характеризуется рядом параметров
сотрудников, которые должны быть назначены на выполнение этих работ. Каждый j-й сотрудник характеризуется рядом параметров 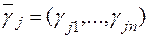 . Заданы коэффициенты
. Заданы коэффициенты 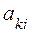 значимости i-го параметра,
значимости i-го параметра, 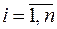 , при выполнении k-й работы,
, при выполнении k-й работы, 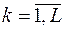 .
.
Найти оптимальное распределение работ между сотрудниками.
Задача оптимального резервирования
Система состоит из n элементов. Определить x j − число элементов j-го типа 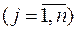 , минимизирующее суммарные затраты на резерв при заданном ограничении d на показатель надежности системы, если d j – затраты на один элемент j-го типа,
, минимизирующее суммарные затраты на резерв при заданном ограничении d на показатель надежности системы, если d j – затраты на один элемент j-го типа, 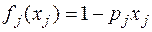 − значение показателя надежности по j‑му типу элемента (p j − вероятность отказа элемента j-го типа).
− значение показателя надежности по j‑му типу элемента (p j − вероятность отказа элемента j-го типа).
Дата: 2019-02-25, просмотров: 505.