Интегралы от неограниченной функции (иначе несобственные интегралы 2-го рода) на интервале 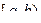 определяются формулами:
определяются формулами:
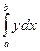 =│Здесь =│Здесь 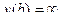 │= │= 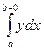
| (2.1) |
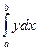 =│Здесь =│Здесь 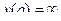 │= │= 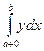
| (2.2) |
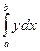 =│Здесь =│Здесь 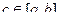 и и 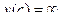 │= │= 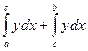
| (2.3) |
В этих формулах:
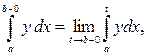
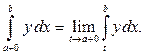
Когда 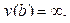 говорят, что точка
говорят, что точка 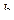 является особой точкой, или особенностью для функции
является особой точкой, или особенностью для функции 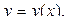
Геометрический смысл формул (2.1) – (2.3) показан на рис. 2.1 – 2.3.



Рис. 2.1 Рис. 2.2 Рис. 2.3
При 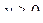 формулы (2.1) – (2.3) имеют следующий смысл:
формулы (2.1) – (2.3) имеют следующий смысл:
– формула (2.1) даёт площадь криволинейной трапеции, бесконечно растянувшейся вдоль вертикали 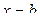 (рис. 2.1);
(рис. 2.1);
– формула (2.2) даёт площадь криволинейной трапеции, бесконечно растянувшейся вдоль вертикали 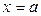 (рис. 2.2);
(рис. 2.2);
– формула (2.3) даёт площадь криволинейной трапеции, бесконечно растянувшейся вдоль вертикали 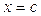 (рис. 2.3).
(рис. 2.3).
З а д а ч а 4. Выясните, сходится ли несобственный интеграл 2-го рода 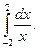
□ 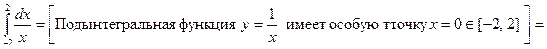
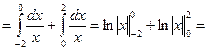
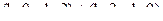
 не существует.
не существует.
Следовательно, данный интеграл расходится (значение 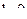 не существует, поэтому выражение
не существует, поэтому выражение 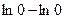 не имеет смысла: вычитать можно только числа). ■
не имеет смысла: вычитать можно только числа). ■
Несобственные интегралы 1-го и 2-го рода можно записать одним символом
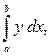
в котором, например, при  получается интеграл (1.1), а при
получается интеграл (1.1), а при 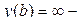 интеграл (2.1).
интеграл (2.1).
Тренировка по теме «Интегралы от неограниченной функции»
Вычислить несобственный интеграл или доказать его расходимость
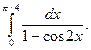
1) 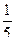 2)
2)  3)
3) 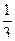 4)
4) 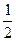 5) Расходится
5) Расходится
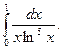
1) 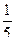 2)
2)  3)
3) 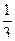 4)
4) 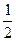 5) Расходится
5) Расходится
Сходимость несобственного интеграла
От степенной функции
Интеграл 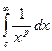
| сходится при 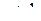 расходится при
расходится при 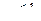
| (3.1) |
Интеграл 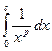
| сходится при 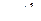 расходится при расходится при 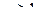
| (3.2) |
¨ При 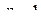 получаем
получаем
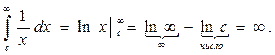 Значит, этот интеграл расходится. Рассмотрим интеграл (3.1) при остальных значениях
Значит, этот интеграл расходится. Рассмотрим интеграл (3.1) при остальных значениях 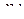
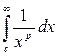 =
= 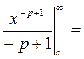
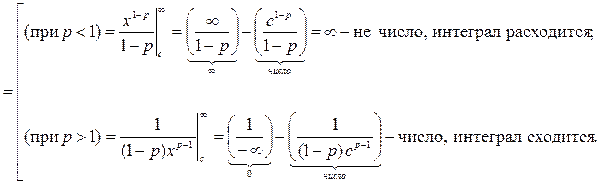
Утверждение (3.1) полностью доказано. Займёмся интегралом (3.2):
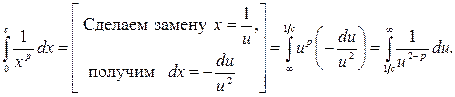
Получился интеграл вида (3.1); он сходится при 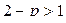 (при этом
(при этом 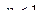 ) и расходится при других
) и расходится при других 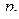 ■
■
З а д а ч а 1. Сходится ли несобственный интеграл 1-го рода 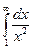 ?
?
□ Здесь 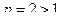 , поэтому, согласно формуле (3.1), данный интеграл сходится. ■
, поэтому, согласно формуле (3.1), данный интеграл сходится. ■
З а д а ч а 2. Сходится ли несобственный интеграл 2-го рода 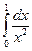 ?
?
□ Здесь 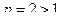 , поэтому, согласно (3.2), данный интеграл расходится. ■
, поэтому, согласно (3.2), данный интеграл расходится. ■
П р и м е ч а н и е. Несобственные интегралы
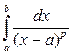 ,
, 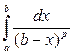
приводятся к выражению (28.2), если выполнить соответствующую замену 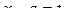 или
или 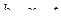 .
.
Тренировка по теме
«Сходимость несобственного интеграла от степенной функции»
Вычислить несобственный интеграл или доказать его расходимость
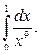
1) 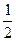 2)
2)  3)
3) 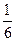 4)
4) 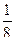 5) Расходится
5) Расходится
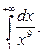
1) 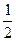 2)
2)  3)
3) 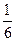 4)
4) 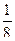 5) Расходится
5) Расходится
[1] Ньютон Исаак (1642-1727) – английский физик и математик. Открыл закон всемирного тяготения, сформулировал основные законы механики, изобрёл зеркальный телескоп.
Лейбниц Готфрид Вильгельм (1646-1716) – немецкий математик, философ, физик, юрист, историк. Ввёл современные знаки дифференциала и интеграла.
[2] Интегрировать (лат.) – восстанавливать.
[3] Аналогичные равносильности имеются в школьной математике. Например, чтобы решать уравнения вида 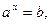 люди придумали логарифмы и пишут
люди придумали логарифмы и пишут 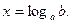 Поэтому выражения
Поэтому выражения 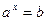 и
и 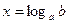 равносильны друг другу (при
равносильны друг другу (при 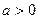 и
и 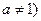 .
.
Дата: 2019-02-25, просмотров: 311.