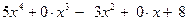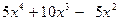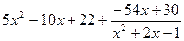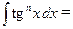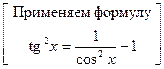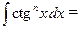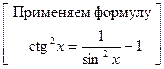Выражение
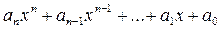
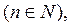
в котором 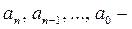 числа, называется многочленом (или полиномом) степени n относительно переменной x.
числа, называется многочленом (или полиномом) степени n относительно переменной x.
Пример: выражение 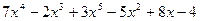 есть многочлен степени 5 (5 – наибольшая степень у переменной
есть многочлен степени 5 (5 – наибольшая степень у переменной 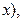 поэтому многочлен можно обозначить
поэтому многочлен можно обозначить 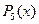 .
.
Пусть 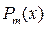 – многочлен степени
– многочлен степени 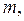
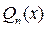 – многочлен степени
– многочлен степени 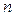 .
.
Отношение многочленов
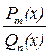
называется рациональной дробью. Если 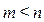 , дробь называется правильной. В остальных случаях рациональная дробь называется неправильной.
, дробь называется правильной. В остальных случаях рациональная дробь называется неправильной.
Примеры: 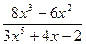 – правильная рациональная дробь;
– правильная рациональная дробь;
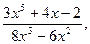
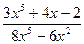 – неправильные рациональные дроби.
– неправильные рациональные дроби.
Если интегрируется неправильная рациональная дробь, сначала её нужно записать в виде суммы:
| Неправильная рациональная дробь = = многочлен + правильная рациональная дробь. |
З а д а ч а 1. Неправильную рациональную дробь 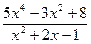 запишите в виде суммы многочлена и правильной рациональной дроби.
запишите в виде суммы многочлена и правильной рациональной дроби.
□ Разделим числитель на знаменатель:
| _ | 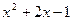
| |
|
| ||
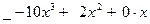
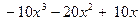
| ||
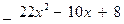
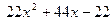
| ||
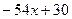
| (остаток) |
Отсюда
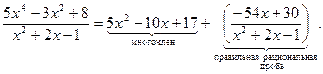 ■
■
Чтобы проинтегрировать правильную рациональную дробь, её тоже сначала нужно разложить:
| Правильная рациональная дробь = сумма элементарных дробей. |
З а д а ч а 2. Какой вид имеет разложение правильной рациональной функции
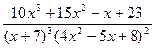
на сумму элементарных дробей?
□ Внимательно посмотрите на метод разложения:
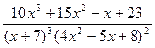 =
= 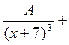
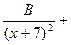
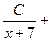
+ 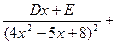
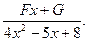 ■
■
Буквы A , B , C , D , E , F , G обозначают числа, способ определения которых показан в задаче 3. Очевидно, вы заметили: в знаменателях правой части показатели степеней постепенно убывают.
З а д а ч а 3. Правильную рациональную функцию 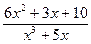 разложите на сумму элементарных дробей.
разложите на сумму элементарных дробей.
□ 1-й шаг - разложим знаменатель на множители: 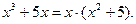
Поэтому 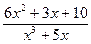
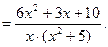
2-й шаг - дробь разложим на сумму элементарных дробей:
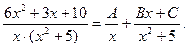 (а)
(а)
3-й шаг – определим значения 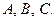
Сначала обе части умножим на общий знаменатель 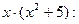
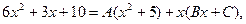
и раскроем скобки:
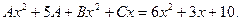
Теперь приравняем члены с одинаковыми степенями:
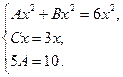
Сократим первое уравнение на 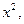 второе – на
второе – на 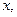 третье – на 5:
третье – на 5:
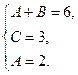
Находим 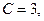
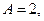
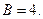
4-й шаг - подставим эти числа в (а) и получим результат
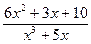
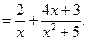 ■
■
З а д а ч а 4. Найдите интеграл 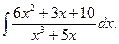
□ 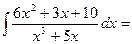 │Выполняем все шаги, указанные в решении задачи 3│=
│Выполняем все шаги, указанные в решении задачи 3│=
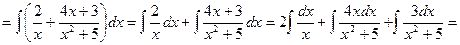
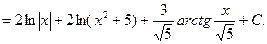 ■
■
Тренировка по теме «Элементарная дробь, её интегрирование»
Найдите интегралы.
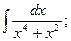
1) 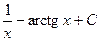 2)
2) 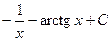 3)
3) 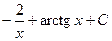 4)
4) 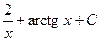
5) 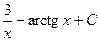
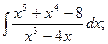
1) 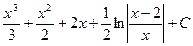 2)
2) 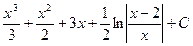
3) 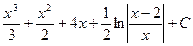 4)
4) 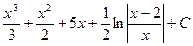
5) 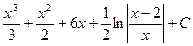
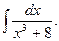
1) 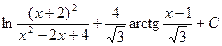 2)
2) 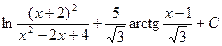
3) 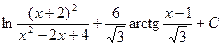 4)
4) 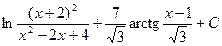
5) 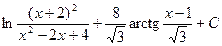
Интегрирование некоторых типов
Тригонометрических выражений
Рассмотрим способы вычисления интегралов, содержащих тригонометрические функции.
1 )
|
| 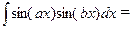 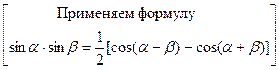
|
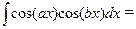 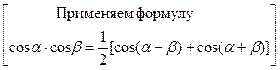
| |
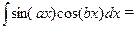 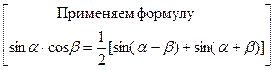
|
З а д а ч а 1. Найдите 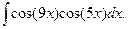
□ 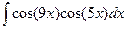 =
= 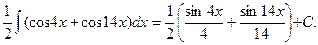 ■
■
2 )
|
|
|
|
З а д а ч а 2. Найдите 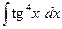 .
.
□ 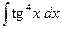
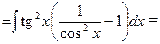
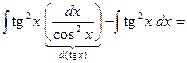
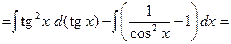
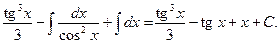 ■
■
3 )
| а) Если m – нечётное число, делаем замену t = cos x, если же n – нечётное число, делаем замену t = sin x. | |
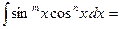
|
б) Если m и n – чётные числа, применяем формулы
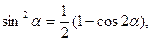 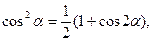 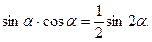
|
в) Если 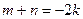 ( ( 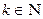 ), делаем замену t = tg x,
тогда ), делаем замену t = tg x,
тогда 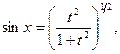 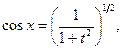 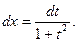
| |
З а д а ч а 3. Найдите 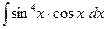 .
.
□ 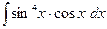 =│Сделаем замену
=│Сделаем замену 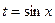 │
│ 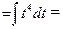
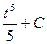
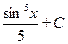 . ■
. ■
З а д а ч а 4. Найдите 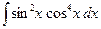 .
.
□ 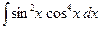 =
= 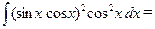
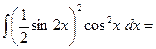
= 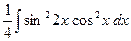 =
= 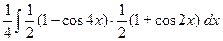
= 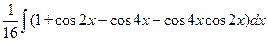 =│Но
=│Но 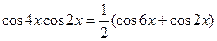 │=
│=
= 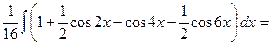
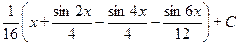 . ■
. ■
З а д а ч а 5. Найдите 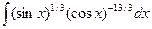 .
.
□ 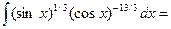
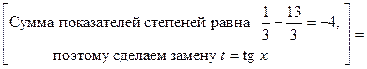
= 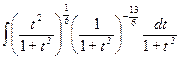 =
= 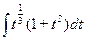 =
=
= 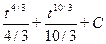 =
= 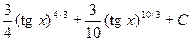 . ■
. ■
4) Пусть символ 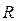 обозначает рациональную функцию от своих аргументов. Интегрировать функцию
обозначает рациональную функцию от своих аргументов. Интегрировать функцию 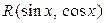 можно с помощью следующей замены:
можно с помощью следующей замены:
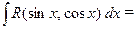
| Делаем замену 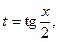 тогда
тогда 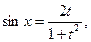 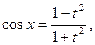 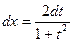
|
Замена 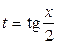 называется универсальной тригонометрической подстановкой. Она может приводить к громоздким выкладкам, поэтому к ней прибегают, когда ни один из предыдущих методов не подходит.
называется универсальной тригонометрической подстановкой. Она может приводить к громоздким выкладкам, поэтому к ней прибегают, когда ни один из предыдущих методов не подходит.
З а д а ч а 5. Найдите 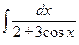 .
.
□ 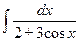 =
= 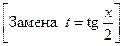 =
= 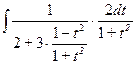 =
=
= 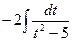 =
= 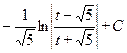 =
= 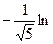
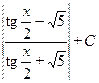 . ■
. ■
Тренировка по теме
«Интегрирование некоторых типов тригонометрических выражений»
Найдите интегралы.
а) 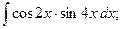
1) 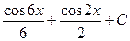 2)
2) 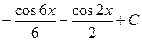 3)
3) 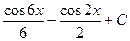
4) 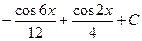 5)
5) 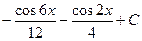
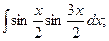
1) 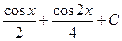 2)
2) 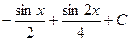 3)
3) 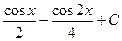
4) 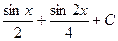 5)
5) 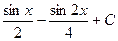
б) 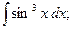
1) 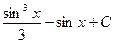 2)
2) 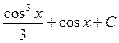 3)
3) 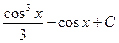
4) 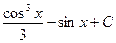 5)
5) 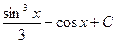
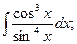
1) 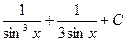 2)
2) 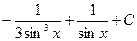 3)
3) 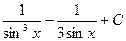
4) 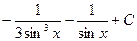 5)
5) 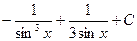
в) 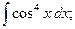
1) 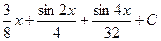 2)
2) 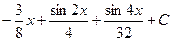 3)
3) 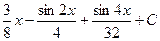
4) 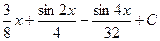 5)
5) 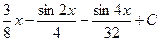
г) 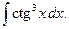
1) 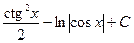 2)
2) 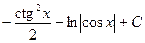 3)
3) 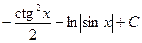
4) 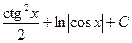 5)
5) 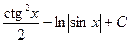
Дата: 2019-02-25, просмотров: 311.