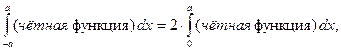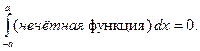Докажем следующее равенство:
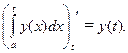
|
(2.1)
 ¨ Рассмотрим интеграл
¨ Рассмотрим интеграл 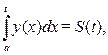 (а) дающий площадь криволинейной трапеции на участке
(а) дающий площадь криволинейной трапеции на участке 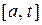 (рис.2.1). Если будем перемещать точку
(рис.2.1). Если будем перемещать точку 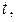 будет меняться и площадь
будет меняться и площадь 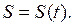 При смещении от точки
При смещении от точки 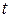 на раcстояние
на раcстояние 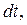 как показано на рис. 2.1, Рис. 2.1
как показано на рис. 2.1, Рис. 2.1
добавится площадь 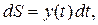 поэтому
поэтому
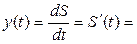 (а)
(а) 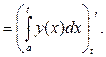 ■
■
Равенство (2.1) будет использовано при выводе формулы (4.1).
Тренировка по теме
«Производная интеграла по переменному верхнему пределу»
1. а) Найдите производную 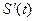 от функции
от функции 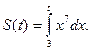
1) 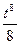 2)
2) 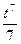 3)
3) 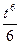 4)
4) 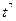 5)
5) 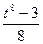
б) Найдите производную по переменной 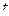 от функции
от функции 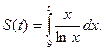
1) 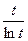 2)
2) 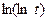 3)
3) 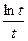 4)
4) 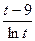 5)
5) 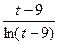
3. Знак двойной подстановки
Далее будем применять символ 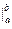 – знак двойной подстановки:
– знак двойной подстановки:
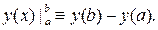 (3.1)
(3.1)
Примеры: 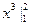 = 23–13 = 7,
= 23–13 = 7,
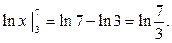
Из (3.1) получаются следующие свойства знака двойной подстановки:
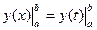
| Аргумент можно обозначать любой буквой. | (3.2) |
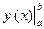 = = 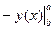
| (3.3) | |
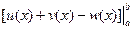 = = 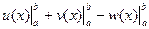
| (3.4) | |
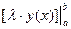 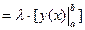
| Здесь 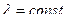
| (3.5) |
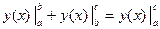
| (3.6) |
¨ Доказательство этих равенств элементарно. Чтобы убедиться в этом, покажем доказательство формул (3.2) и (3.6).
В правой части выражения (3.1) отсутствует аргумент 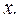 Поэтому аргумент левой части вы можете обозначать любой буквой. Так получается равенство (3.2).
Поэтому аргумент левой части вы можете обозначать любой буквой. Так получается равенство (3.2).
Доказательство равенства (3.6):
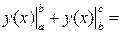
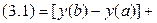
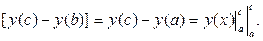 ■
■
Тренировка по теме «Знак двойной подстановки»
1. Найдите значения.
а) 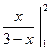
1) 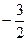 2)
2) 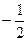 3)
3) 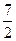 4)
4) 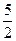 5)
5) 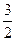
б) 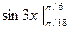
1) 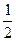 2)
2) 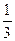 3)
3)  4)
4) 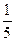 5)
5) 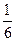
2. Найдите значения 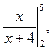
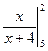 и убедитесь в справедливости равенства (3.3).
и убедитесь в справедливости равенства (3.3).
1) 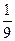 и
и 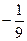 2)
2) 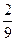 и
и 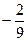 3)
3) 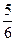 и
и 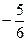 4)
4) 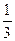 и
и 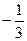 5)
5) 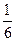 и
и 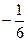
3. Найдите значение 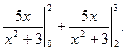
1) 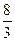 2)
2) 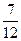 3)
3) 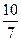 4)
4) 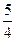 5)
5) 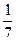
4. Связь определённого интеграла с неопределённым
Теперь докажем формулу, означающую, что определённый интеграл можно вычислить с помощью неопределённого:
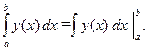
|
| Формула Ньютона-Лейбница. |
(4.1)
¨ (2.1) 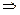
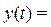
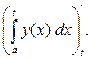 (а)
(а)
Проинтегрируем обе части:
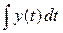 =
= 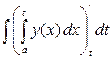 = (1.5) =
= (1.5) = 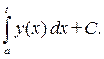 (б)
(б)
Левый интеграл обозначим 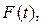 т. е. пусть
т. е. пусть 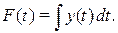 (в)
(в)
(б) 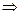
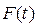 =
= 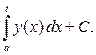 (г)
(г)
(г) 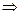
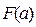 =
= 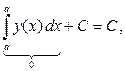 т. е.
т. е. 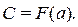 (д)
(д)
(г) 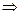
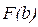 =
= 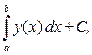 отсюда
отсюда
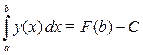 = (д) =
= (д) = 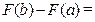 (3.1)
(3.1) 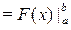 = (в) =
= (в) = 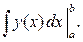 ■
■
З а д а ч а 1. Вычислите 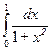 .
.
□ 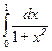 = (4.1) =
= (4.1) = 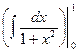 =
= 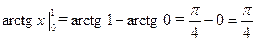 . ■
. ■
Тренировка по теме «Связь определённого интеграла с неопределённым»
Вычислите определённые интегралы.
а) 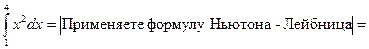
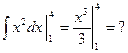
1) 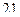 2)
2) 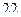 3)
3) 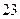 4)
4) 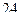 5)
5) 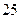
б) 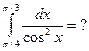
1) 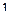 2)
2) 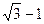 3)
3) 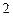 4)
4) 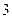 5)
5) 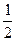
Свойства определённого интеграла
При вычислении, исследовании определённого интеграла могут пригодиться следующие свойства определённого интеграла:
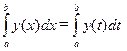
| Переменную интегрирования можно обозначать любой буквой. | (5.1) |
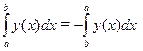
| Если переставить пределы интегрирования, интеграл умножится на -1. | (5.2) |
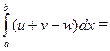 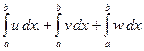
| Интеграл от суммы (разности) равен сумме (разности) интегралов. | (5.3) |
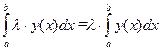
| Постоянный множитель можно вынести за знак интеграла. | (5.4) |
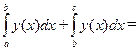 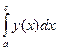
| Свойство аддитивности, или сложения. | (5.5) |
|
| (5.6) | |
¨ Свойства (5.1) – (5.5) вытекают из соответствующих свойств знака двойной подстановки. В качестве примера докажем формулу (5.5):
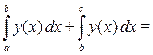
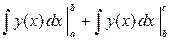 = (3.6) =
= (3.6) = 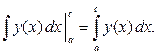
Докажем равенства (5.6). Если 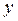 – чётная функция (рис. 5.1), то
– чётная функция (рис. 5.1), то
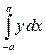 =│Фигура симметрична относительно оси
=│Фигура симметрична относительно оси 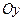 │=
│= 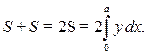
Если же 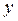 – нечётная функция (рис. 5.2), то
– нечётная функция (рис. 5.2), то
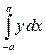 =│Фигура симметрична относительно точки
=│Фигура симметрична относительно точки 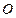 │=
│= 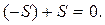 ■
■


Рис. 5.1 Рис. 5.2
Примеры: 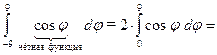
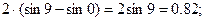
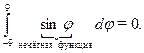
Тренировка по теме «Свойства определённого интеграла»
Найдите интегралы.
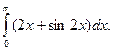
1) 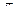 2)
2) 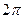 3)
3) 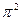 4)
4) 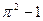 5)
5) 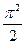
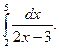
1) 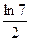 2)
2) 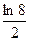 3)
3) 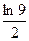 4)
4) 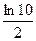 5)
5) 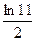
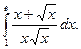
1) 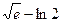 2)
2) 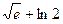 3)
3) 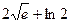 4)
4) 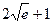 5)
5) 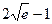
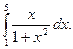
1) 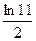 2)
2) 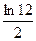 3)
3) 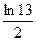 4)
4) 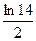 5)
5) 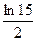
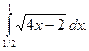
1) 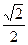 2)
2) 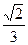 3)
3) 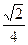 4)
4) 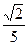 5)
5) 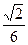
Вычисление определённого интеграла
С помощью замены переменной
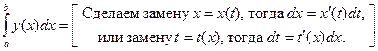 = = 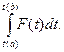
|
¨ 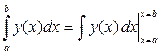 =│Сделаем замену
=│Сделаем замену 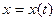 или
или 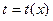 │=
│=
= 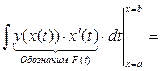
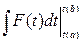
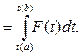 ■
■
З а д а ч а 1. Найдите 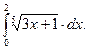
□ 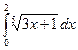 =
= 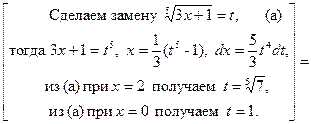
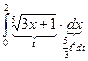 =
=
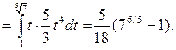 ■
■
Тренировка по теме
«Вычисление определённого интеграла с помощью замены переменной»
Найдите интегралы.
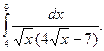
1) 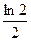 2)
2) 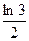 3)
3) 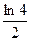 4)
4) 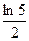 5)
5) 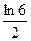
№ 9.1.47. 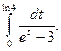
1) 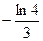 2)
2) 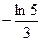 3)
3) 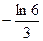 4)
4) 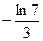 5)
5) 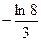
№ 9.1.48. 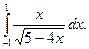
1) 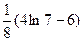 2)
2) 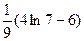 3)
3) 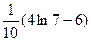 4)
4) 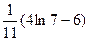 5)
5) 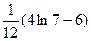
Частичное интегрирование
В определённом интеграле
Частичное интегрирование (или интегрирование по частям) ведётся по формуле
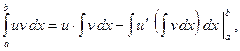
|
(7.1)
которую можно записать в виде
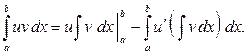
¨ Применив к формуле (5.1-1) формулу (4.1), сразу получим (7.1). ■
 З а д а ч а 1. Найдите площадь криволинейной трапеции, ограниченной линией
З а д а ч а 1. Найдите площадь криволинейной трапеции, ограниченной линией 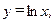 осью
осью 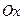 и прямыми
и прямыми 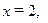
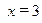 .
.
□ Нарисуем фигуру 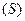 (рис.7.1) и вычислим её пло-
(рис.7.1) и вычислим её пло-
щадь:
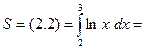
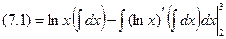 =
=
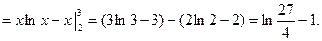 ■ Рис. 7.1
■ Рис. 7.1
Тренировка по теме «Частичное интегрирование в неопределённом интеграле»
Найдите интегралы.
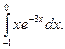
1) 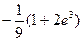 2)
2) 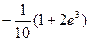 3)
3) 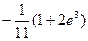 4)
4) 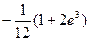 5)
5) 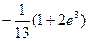
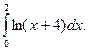
1) 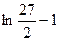 2)
2) 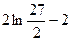 3)
3) 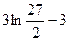 4)
4) 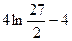 5)
5) 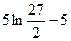
Среднее значение функции
Пусть дана функция 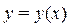 и на интервале
и на интервале 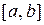 построен
построен
её график (рис. 8.1). Площадь фигуры будет равна 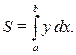 (а)
(а)


Рис. 8.1 Рис. 8.2
Выровняем верхнюю границу фигуры, сохранив её площадь (рис. 8.2). Получится прямоугольник, площадь которого 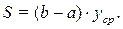 (б)
(б)
Приравняв правые части формул (а), (б), получим
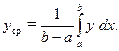
|
Формула вычисления среднего значения функции 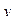 на интервале
на интервале 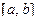 . .
|
(8.1)
З а д а ч а 1. Найдите среднее значение функции 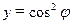 при
при 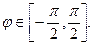
□ 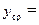
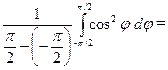
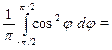
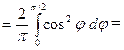
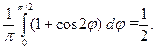 ■
■
З а д а ч а 2. По проводнику с сопротивлением 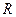 течёт переменный электрический ток
течёт переменный электрический ток 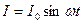 (
( 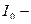 амплитуда,
амплитуда, 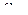 круговая частота колебаний тока). Найдите среднее значение мощности тока. (Справка. Используйте полученный в физике результат: мгновенное значение мощности электрического тока определяется по формуле
круговая частота колебаний тока). Найдите среднее значение мощности тока. (Справка. Используйте полученный в физике результат: мгновенное значение мощности электрического тока определяется по формуле 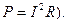
□ Подставим значение 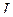 в формулу мощности:
в формулу мощности: 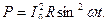 Так как
Так как 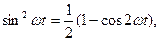 то
то 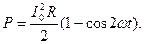 Теперь находим среднее значение мощности тока за произвольный промежуток времени
Теперь находим среднее значение мощности тока за произвольный промежуток времени 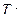
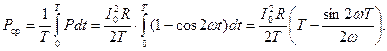 (а)
(а)
Покажем, что 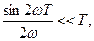 а потому член
а потому член 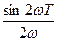 можно отбросить. Для технических целей применяется переменный ток частотой 50 Гц. В этом случае круговая частота
можно отбросить. Для технических целей применяется переменный ток частотой 50 Гц. В этом случае круговая частота 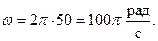 Отсюда
Отсюда
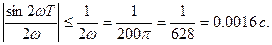
Обычное время 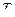 наблюдения человека за мощностью тока намного превышает крошечную величину
наблюдения человека за мощностью тока намного превышает крошечную величину 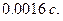 поэтому эту величину действительно можно отбросить. Тогда из (а) получим
поэтому эту величину действительно можно отбросить. Тогда из (а) получим
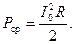 ■
■
Тренировка по теме «Среднее значение функции»
Решите задачи.
а) Вычислите среднее значение функции 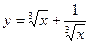 на интервале [1, 8].
на интервале [1, 8].
1) 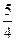 2)
2) 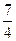 3)
3) 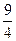 4)
4) 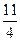 5)
5) 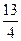
б) Вычислите среднее значение функций 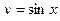 и
и 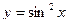 на интервале
на интервале 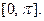
1) 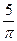 и
и 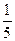 2)
2) 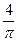 и
и 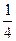 3)
3) 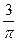 и
и 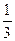 4)
4) 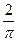 и
и 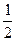 5)
5) 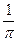 и
и 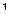
Тесты по опред.интегралам.
Глава 3
Дата: 2019-02-25, просмотров: 346.