Принцип составления определённого интеграла
При нахождении физической или геометрической величины определённый интеграл появляется естественным путём:
вы находите бесконечно малый кусочек величины и интегрированием получаете всю эту величину.
Именно таким путём получилась формула вычисления площади (1.1-2). Посмотрите ещё раз, как применяется этот принцип при решении следующей физической задачи.
Имеется тело, которое движется вдоль оси 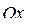 под действием силы
под действием силы 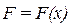 , направленной также вдоль оси
, направленной также вдоль оси 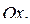 Определите работу, совершаемую этой силой на отрезке
Определите работу, совершаемую этой силой на отрезке 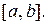
□ Внутри 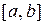 около произвольной точки
около произвольной точки 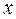 выделим бесконечно малый участок длины
выделим бесконечно малый участок длины 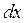 (рис. 1.1). Из-за малости
(рис. 1.1). Из-за малости 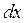 сила на этом участке не успевает заметно измениться. Поэтому полагаем силу постоянной и работа на участке
сила на этом участке не успевает заметно измениться. Поэтому полагаем силу постоянной и работа на участке 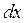 будет равна
будет равна

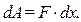
Проинтегрировав по отрезку 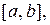 получим формулу вычисления работы на этом отрез- Рис. 1.1
получим формулу вычисления работы на этом отрез- Рис. 1.1
ке:
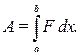 ■ (1.1)
■ (1.1)
З а д а ч а 1. Найдите работу, совершаемую силой  на отрезке [2, 4] оси
на отрезке [2, 4] оси 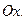
□ 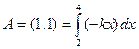
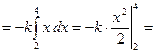
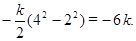 ■
■
Тренировка по теме «Принцип составления определённого интеграла»
42. Решите задачи.
А) Представьте себе, что вы имеете функцию 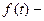 скорость нагревания тела (изменение температуры тела за единицу времени). На сколько градусов
скорость нагревания тела (изменение температуры тела за единицу времени). На сколько градусов 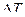 нагреется тело за промежуток времени от
нагреется тело за промежуток времени от 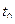 до
до 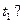 (Ответ запишите через определённый интеграл).
(Ответ запишите через определённый интеграл).
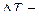
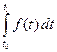
Б) Представьте себе, что вы имеете функцию 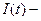 зависимость величины электрического тока от времени. Какое количество электричества
зависимость величины электрического тока от времени. Какое количество электричества 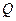 пройдёт через проводник за промежуток времени от
пройдёт через проводник за промежуток времени от 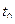 до
до 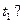 (Ответ запишите через определённый интеграл).
(Ответ запишите через определённый интеграл).
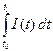
Площадь плоской фигуры
Фигура называется плоской, если всю её, не деформируя, можно расположить на плоскости.
Площади фигур 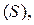 указанных на рис. 2.1 – 2.3, вы можете найти по следующим формулам:
указанных на рис. 2.1 – 2.3, вы можете найти по следующим формулам:
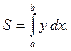
| Площадь фигуры, прилегающей к оси 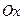 сверху. сверху.
| (2.1) |
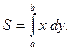
| Площадь фигуры, прилегающей к оси 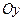 справа. справа.
| (2.2) |
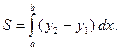
| Площадь фигуры, ограниченной линиями 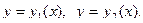
| (2.3) |
¨ Формула (2.1) была получена ранее (равенство (1.1-2). Формула (2.2) следует из формулы (2.1), если переменные 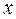 и
и 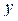 поменять ролями.
поменять ролями.




Рис. 2.1 Рис. 2.2 Рис. 2.3 Рис. 2.4
На рис. 2.3 площадь 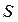 равна разности площадей под линиями
равна разности площадей под линиями 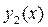 и
и 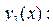
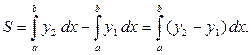
Получилась формула (2.3). ■
З а д а ч а 1. Найдите площадь фигуры, ограниченной параболой 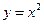 и прямой
и прямой 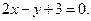
□ Составим систему уравнений 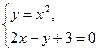 и получим
и получим 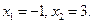
Фигура  ограниченная линиями
ограниченная линиями 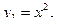
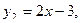 показана на рис. 2.7.
показана на рис. 2.7.
Её площадь
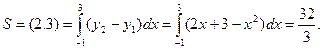 ■
■
Тренировка по теме «Площадь плоской фигуры»
Найдите площадь фигур, ограниченных данными линиями.
а) 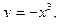
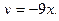
1) 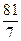 2)
2) 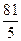 3)
3) 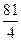 4)
4) 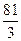 5)
5) 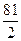
в) 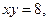
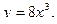
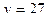
1) 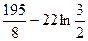 2)
2) 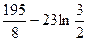 3)
3) 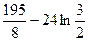 4)
4) 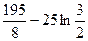 5)
5) 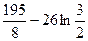
Длина плоской линии
Линию называют плоской, если всю её, не деформируя, можно расположить на плоскости, например, на плоскости 
Длину линий, показанных на рис. 3.1 – 3.2, вы можете найти по следующим формулам:
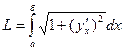
| – длина линии 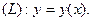
| (3.1) |
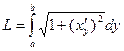
| – длина линии 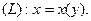
| (3.2) |



Рис. 3.1 Рис. 3.2 Рис. 3.3
¨ На рис. 3.3 показан в увеличенном масштабе прямоугольный треугольник, примыкающий к бесконечно малому кусочку линии 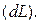
Применив к треугольнику формулу Пифагора, получим длину бесконечно малого кусочка линии в декартовых координатах:
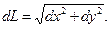
|
(3.3)
Величина 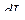 называется также дифференциалом длины линии.
называется также дифференциалом длины линии.
Если 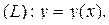 то
то 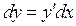 и подстановка
и подстановка 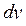 в (3.3) даёт
в (3.3) даёт
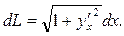 (3.4)
(3.4)
Если 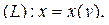 то
то 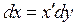 и подстановка
и подстановка 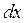 в (3.3) даёт
в (3.3) даёт
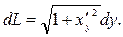 ■ (3.5)
■ (3.5)
З а д а ч а 1. Найдите длину линии 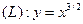 при
при 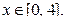
□ 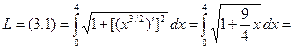
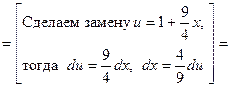
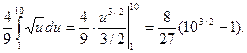 ■
■
Тренировка по теме «Длина плоской линии»
Найдите длину линии.
а) 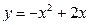 от вершины параболы до точки с абсциссой
от вершины параболы до точки с абсциссой 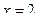
1) 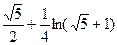 2)
2) 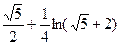 3)
3) 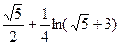 4)
4) 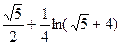 5)
5) 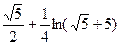
б) 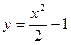 между точками пересечения с осью абсцисс.
между точками пересечения с осью абсцисс.
1) 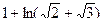 2)
2) 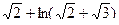 3)
3) 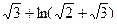 4)
4) 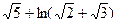
5) 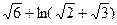
Объём тела
Объём тела 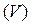 можно найти по одной из следующих формул:
можно найти по одной из следующих формул:
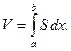
| Здесь 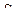 площадь сечения тела плоскостью,
перпендикулярной к оси площадь сечения тела плоскостью,
перпендикулярной к оси  (рис. 4.1). (рис. 4.1).
| (4.1) |
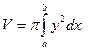
| Объём тела вращения вокруг оси  (рис. 4.2). (рис. 4.2).
| (4.2) |

Рис. 4.1 Рис. 4.2
¨ Дано тело 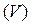 и ось
и ось 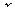 в пространстве (рис. 4.1).
в пространстве (рис. 4.1).
 Плоскостями, перпендикулярными оси
Плоскостями, перпендикулярными оси 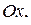 мысленно рассечём
мысленно рассечём 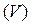 на ломтики бесконечно малой толщины
на ломтики бесконечно малой толщины 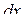 Посмотрите на один такой кусочек (рис. 4.3). Из-за малости
Посмотрите на один такой кусочек (рис. 4.3). Из-за малости 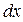 площадь
площадь 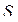 сечения не успевает заметно измениться, поэтому считаем
сечения не успевает заметно измениться, поэтому считаем 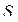 постоянной на участке
постоянной на участке 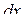 Ломтик представляет собой цилиндр с основанием
Ломтик представляет собой цилиндр с основанием 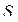 и высотой
и высотой 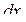 Его объём равен
Его объём равен 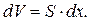 Проинтегрировав это выражение, получим формулу (4.1).
Проинтегрировав это выражение, получим формулу (4.1).
Когда фигура 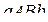 вращается вокруг оси
вращается вокруг оси 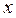 (или вокруг какой-нибудь другой прямой), получается тело вра- Рис. 4.3
(или вокруг какой-нибудь другой прямой), получается тело вра- Рис. 4.3
щения вокруг оси 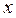 (рис. 4.2). В сечении, перпендику-
(рис. 4.2). В сечении, перпендику-
лярном оси 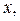 будет круг
будет круг 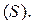 Его радиус равен
Его радиус равен 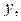 поэтому площадь
поэтому площадь 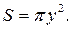 Подставив
Подставив 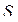 в (4.1), получим (4.2). ■
в (4.1), получим (4.2). ■
З а д а ч а 1. Найдите объём шарового сегмента высотой h, отсечённого от шара радиуса R .
□ Нарисуем систему координат  как показано на рис. 4.4.
как показано на рис. 4.4.
П е р в ы й с п о с о б. Уравнение сферы (поверхности шара) таково:
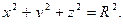
Между точками M и R возьмём произвольную точку 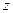 и проведём через неё
и проведём через неё
 плоскость
плоскость 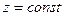 перпендикулярно Oz .
перпендикулярно Oz .
В сечении получится круг. Уравнение
окружности, ограничивающей этот круг
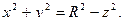
Значит, радиус этого круга 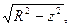
а площадь 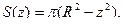
Так как 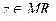 а точка
а точка 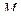 находится на
находится на
высоте 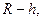 то
то 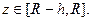
По формуле (4.1) получаем
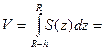
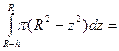
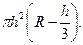
Итак, объём шарового сегмента равен
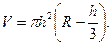
Рис. 4.4
В т о р о й с п о с о б. Шаровой сегмент
представляет собой тело вращения вокруг оси  Лежащая на плоскости
Лежащая на плоскости  линия
линия 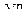 (часть окружности) имеет уравнение
(часть окружности) имеет уравнение 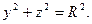 Отсюда
Отсюда 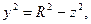 где
где 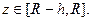 По формуле (4.2) будем иметь
По формуле (4.2) будем иметь 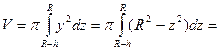
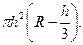 ■
■
Заметим, что если 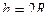 получится
получится 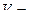
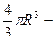 объём всего шара.
объём всего шара.
З а д а ч а 2. Найдите количество бетона, необходимого для возведения опоры моста в виде усечённого конуса. Размеры опоры: высота Н, радиус нижнего основания R, радиус верхнего основания r.
□ Усечённый конус представляет собой тело вращения, получаемое при вращении трапеции 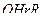 вокруг оси
вокруг оси 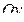 (рис. 4.5). На высоте
(рис. 4.5). На высоте 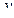 радиус
радиус 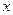 поперечного сечения равен
поперечного сечения равен
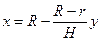
(из подобия треугольников 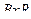 и
и 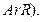 где
где 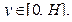 По формуле (4.2) будем иметь
По формуле (4.2) будем иметь
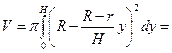
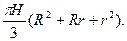
Получилась известная формула объёма усечённого конуса. Итак, количество необходимого бетона
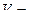
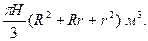 ■
■
В частности, если 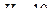 м,
м, 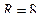 м,
м, 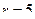 м, плотность
м, плотность 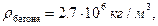 то потребуется
то потребуется 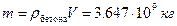 бетона.
бетона.


Рис. 4.5 Рис. 5.1
Тренировка по теме «Объём тела»
Найдите объём тел.
а) Тело ограничено параболическим цилиндром 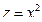 и плоскостями
и плоскостями 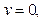
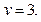
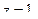
1) 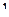 2) 2 3) 3 4) 4 5) 5
2) 2 3) 3 4) 4 5) 5
б) Тело образовано вращением вокруг оси 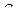 фигуры, ограниченной линиями
фигуры, ограниченной линиями 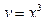
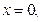
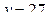 .
.
1) 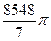 2)
2) 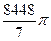 3)
3) 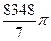 4)
4) 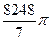 5)
5) 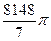
5. Некоторые физические задачи
Задача на вычисление работы
Найдите работу по выкачиванию жидкости плотности 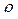 из скважины радиуса
из скважины радиуса 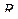 и глубины
и глубины 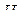
□ Ось 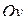 направим вниз, точку
направим вниз, точку 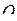 расположим на поверхности земли. Представим себе промежуточный случай: часть жидкости до глубины
расположим на поверхности земли. Представим себе промежуточный случай: часть жидкости до глубины 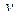 уже выкачена (рис. 5.1). Найдём работу по удалению бесконечно тонкого слоя жидкости толщины
уже выкачена (рис. 5.1). Найдём работу по удалению бесконечно тонкого слоя жидкости толщины 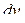 Этот слой представляет собой цилиндр с основанием
Этот слой представляет собой цилиндр с основанием 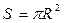 и высотой
и высотой 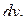 поэтому его объём
поэтому его объём 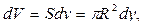 вес
вес 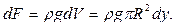 Слой находится на глубине
Слой находится на глубине 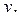 поэтому он будет удалён из скважины, если вы его поднимете на высоту
поэтому он будет удалён из скважины, если вы его поднимете на высоту 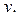 На это уйдёт работа
На это уйдёт работа
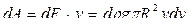
где 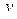 принимает значения от
принимает значения от 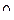 до
до 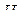 Следовательно,
Следовательно,
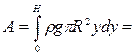
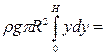
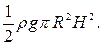 ■
■
Дата: 2019-02-25, просмотров: 292.