Найдите изгибающий момент  в поперечном сечении
в поперечном сечении  горизонтальной балки длины
горизонтальной балки длины 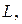 если известно, что балка находится в равновесии под действием опорных реакций
если известно, что балка находится в равновесии под действием опорных реакций 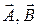 и распределённой вдоль балки нагрузки с интенсивностью
и распределённой вдоль балки нагрузки с интенсивностью 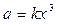 (
(  расстояние от левой опоры,
расстояние от левой опоры, 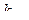 постоянный коэффициент).
постоянный коэффициент).
□ Для наглядности сделаем чертёж (рис. 5.2).
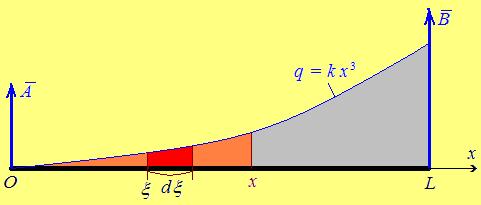
Рис. 5.2
Мысленно отбросим правую часть балки 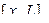 Изгибающий момент в точке
Изгибающий момент в точке  равен сумме моментов всех сил и нагрузок, действующих слева от
равен сумме моментов всех сил и нагрузок, действующих слева от  Момент силы
Момент силы  стремящейся вращать балку по часовой стрелке, положителен и равен
стремящейся вращать балку по часовой стрелке, положителен и равен  Момент, создаваемый нагрузкой на участке
Момент, создаваемый нагрузкой на участке  находящемся на расстоянии
находящемся на расстоянии  от левой опоры (и, значит, на расстоянии
от левой опоры (и, значит, на расстоянии 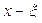 от точки
от точки 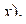 равен
равен

где 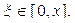 Поэтому момент, создаваемый всей нагрузкой на участке
Поэтому момент, создаваемый всей нагрузкой на участке 
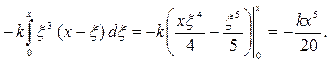
Следовательно,
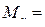

Выразим  через
через 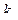 Момент всех сил относительно точки
Момент всех сил относительно точки 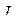 должен равняться 0, потому что балка находится в равновесии, не вращается. Поэтому при
должен равняться 0, потому что балка находится в равновесии, не вращается. Поэтому при  получаем
получаем 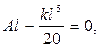
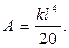 Итак,
Итак,
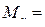
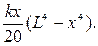 ■
■
Приравняв производную изгибающего момента к нулю, получим 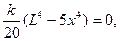

Мы определили опасное сечение – то сечение, в котором изгибающий момент максимален, в котором волокна балки испытывают наибольшие напряжения.
Тренировка по теме «Некоторые физические задачи»
Решите задачи.
а) Рессора прогибается под нагрузкой 2 т на 1.5 см. Какую работу нужно затратить для прогиба рессоры на 3 см? (Сила деформации пропорциональна величине прогиба.)
1) 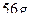 2)
2)  3)
3) 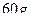 4)
4) 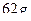 5)
5) 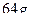
б) Найдите работу, которую нужно затратить, чтобы выкачать жидкость плотности 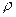 из вертикального цилиндрического резервуара высоты
из вертикального цилиндрического резервуара высоты 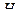 и радиусом основания
и радиусом основания 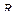
1) 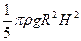 2)
2) 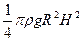 3)
3) 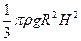 4)
4) 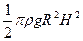 5)
5) 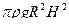
Тесты по применению.
Итоговый тест.
Глава 4
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
| Интеграл от неограниченной функции или с неограниченной областью интегрирования называется несобственным. |
Если несобственный интеграл равен какому-либо числу, он называется сходящимся; в остальных случаях несобственный интеграл называется расходящимся.
Интегралы с неограниченной областью
Интегрирования
Интегралы с неограниченной областью интегрирования (иначе, несобственные интегралы 1-го рода) определяются формулами
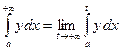
| (1.1) |
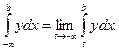
| (1.2) |
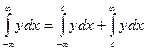
| (1.3) |

 Геометрический смысл равенств (1.1) – (1.3) показан на рис. 1.1 – 1.3. Если
Геометрический смысл равенств (1.1) – (1.3) показан на рис. 1.1 – 1.3. Если 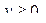 формула (1.1) даёт площадь криволинейной трапеции, бесконечно растянувшейся вдоль оси
формула (1.1) даёт площадь криволинейной трапеции, бесконечно растянувшейся вдоль оси 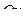 в положительном направлении (рис. 1.1).
в положительном направлении (рис. 1.1).
Рис. 1.1 Рис. 1.2
Аналогично, формула (1.2) даёт площадь криволинейной трапеции, бесконечно растянувшейся вдоль оси 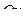 в отрицательном направлении (рис. 1.2). Наконец, формула (1.3) даёт площадь криволинейной трапеции, бесконечно растянувшейся вдоль оси
в отрицательном направлении (рис. 1.2). Наконец, формула (1.3) даёт площадь криволинейной трапеции, бесконечно растянувшейся вдоль оси 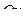 в обоих направлениях (рис. 1.3). В этой формуле число
в обоих направлениях (рис. 1.3). В этой формуле число  можно взять любым (часто берут
можно взять любым (часто берут 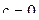 ).
).
 При вычислении несобственного интеграла часто можно обойтись без Рис. 1.3
При вычислении несобственного интеграла часто можно обойтись без Рис. 1.3
знака предела.
З а д а ч а 1. Найдите несобственный интеграл 1-го рода 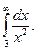
□ 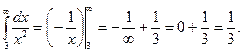 Получилось число, следовательно, данный несобственный интеграл сходится. ■
Получилось число, следовательно, данный несобственный интеграл сходится. ■
З а д а ч а 2. Выясните, сходится ли несобственный интеграл 1-го рода 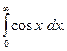
□ 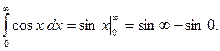 Значение
Значение 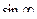 не существует, поэтому этот интеграл расходится. ■
не существует, поэтому этот интеграл расходится. ■
З а д а ч а 3. Найдите потенциал электрического поля, создаваемого зарядом 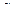 на расстоянии
на расстоянии  от этого заряда.
от этого заряда.
 □ Потенциалом в точке
□ Потенциалом в точке  (обозначим его
(обозначим его
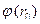 ) называется работа, совершаемая
) называется работа, совершаемая
внешней силой 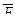 при переносе заряда (+1)
при переносе заряда (+1)
из бесконечности в точку  (рис. 1.4).
(рис. 1.4).
Пусть заряд 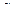 положителен. По закону Рис. 1.4
положителен. По закону Рис. 1.4
Кулона внешняя сила равна 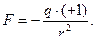 Знак минус написан потому, что внешняя сила направлена противоположно оси
Знак минус написан потому, что внешняя сила направлена противоположно оси 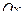 чтобы преодолеть отталкивание одноимённых зарядов. В этом случае
чтобы преодолеть отталкивание одноимённых зарядов. В этом случае
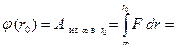
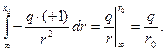 ■
■
Тренировка по теме «Интегралы с неограниченной областью интегрирования»
58. Вычислить несобственный интеграл или доказать его расходимость
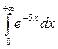
1) 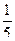 2)
2) 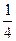 3)
3)  4)
4) 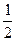 5) Расходится
5) Расходится

1) 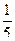 2)
2)  3)
3) 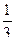 4)
4) 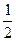 5) Расходится
5) Расходится
Дата: 2019-02-25, просмотров: 425.