Фазовое пространство
Пусть эволюция двумерной ДС задаётся автономной системой ДУ
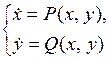 (9.1)
(9.1)
с известными правыми частями, не содержащими 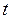 в явном виде. Решив эту систему, получим пару функций
в явном виде. Решив эту систему, получим пару функций
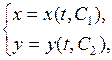 (9.2)
(9.2)
где 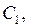
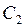 – постоянные. На плоскости введём систему координат
– постоянные. На плоскости введём систему координат 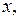
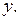 Решение (8.2) изобразится семейством линий.
Решение (8.2) изобразится семейством линий.
Фазовая плоскость – плоскость, на которой координаты 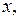
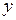 характеризуют состояние ДС.
характеризуют состояние ДС.
Фазовая точка – любая точка фазового пространства.
Фазовая линия (или фазовая траектория) – линия, по которой движется фазовая точка с течением времени.
Выражения (8.2) являются параметрическими уравнениями фазовой линии, если считать 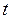 переменным параметром.
переменным параметром.
Фазовый портрет динамической системы – это набор фазовых линий.
Фазовый портрет системы (9.1) получается при различных начальных условиях. Для одномерной ДС фазовый портрет состоит из одной фазовой линии.
Точка покоя (или неподвижная точка, особая точка, состояние равновесия) – фазовая точка, скорость которой равна нулю.
Вектор 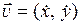 есть скорость фазовой точки. Если фазовая точка неподвижна, то
есть скорость фазовой точки. Если фазовая точка неподвижна, то 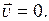 Равенство
Равенство 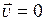 означает, что
означает, что
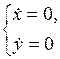 или
или 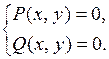
Значит,
Точки покоя двумерной ДС
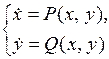 являются корнями системы двух уравнений
являются корнями системы двух уравнений
|
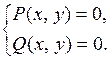
|
З а д а ч а 1. Найти точки покоя ДС, описываемой системой уравнений
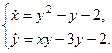
Приравняем правые части нулю:
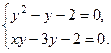
Из первого уравнения 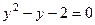 получаем
получаем 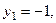
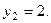 Второе уравнение запишем так:
Второе уравнение запишем так: 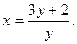 Подстановка значений
Подстановка значений 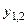 даст соответственно
даст соответственно 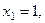
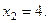 Следовательно, на фазовой плоскости
Следовательно, на фазовой плоскости 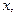
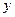 точками покоя являются две точки с координатами
точками покоя являются две точки с координатами 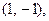
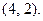 ■
■
Исследование динамической системы на устойчивость
По первому приближению
Дано: динамическая система описывается системой уравнений
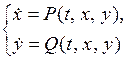 и
и 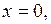 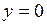 – нулевое решение этой системы. – нулевое решение этой системы.
|
Составляем характеристическое уравнение
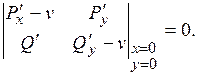 (10.1)
Находим его корни (10.1)
Находим его корни 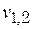 и их вещественные части и их вещественные части 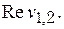 Делаем вывод:
нулевое решение:
- асимптотически устойчиво, если все Делаем вывод:
нулевое решение:
- асимптотически устойчиво, если все 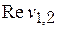 отрицательны;
- неустойчиво, если среди отрицательны;
- неустойчиво, если среди 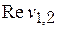 имеется положительное число;
- нужно исследовать другим способом, если среди имеется положительное число;
- нужно исследовать другим способом, если среди 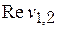 имеется ноль
(критический случай). имеется ноль
(критический случай).
|
З а д а ч а 1. Динамическая система описывается системой уравнений
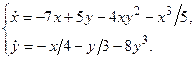
Исследовать точку покоя 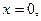
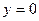 на устойчивость по первому приближению.
на устойчивость по первому приближению.
Выпишем правые части:
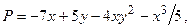
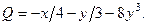
Найдём их частные производные:
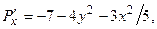
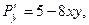
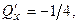
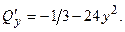
Составим характеристическое уравнение
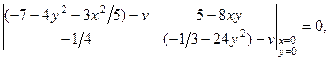 или
или 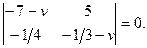
Раскроем определитель
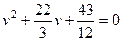 или
или 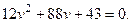
Вычислим корни
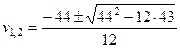 .
.
Оба корня вещественны и отрицательны. Следовательно, точка покоя асимптотически устойчива. ■
Исследование динамической системы на устойчивость
С помощью функции Ляпунова
Дано: динамическая система описывается системой уравнений
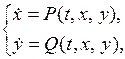
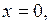 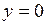 – нулевое решение этой системы, – нулевое решение этой системы,
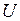 – окрестность начала координат. – окрестность начала координат.
|
Если существует вещественная функция 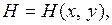 удовлетворяющая условиям
удовлетворяющая условиям
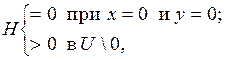 то нулевое решение:
при
то нулевое решение:
при  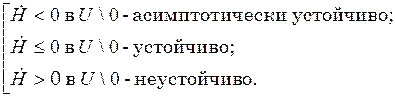
|
Окрестность точки – это какая-либо область, содержащая эту точку. Здесь 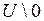 – область, не содержащая начало координат.
– область, не содержащая начало координат.
Функция 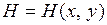 называется функцией Ляпунова.
называется функцией Ляпунова.
З а д а ч а 1. Динамическая система описывается системой уравнений
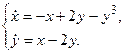
Исследовать нулевое решение 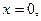
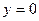 на устойчивость с помощью функции Ляпунова.
на устойчивость с помощью функции Ляпунова.
В качестве функции Ляпунова возьмём
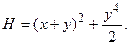
Она удовлетворяет обоим условиям: 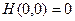 и
и 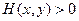 при
при 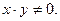 Её производная по времени равна
Её производная по времени равна
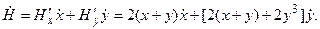
Значения 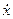 и
и 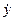 даны в условии задачи. Подставим их:
даны в условии задачи. Подставим их:
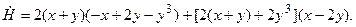
После упрощений получим 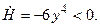 Это значит, что нулевое решение
Это значит, что нулевое решение 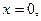
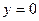 асимптотически устойчиво. ■
асимптотически устойчиво. ■
З а д а ч а 2. Динамическая система описывается системой уравнений
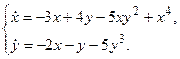
Исследовать нулевое решение 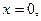
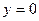 на устойчивость с помощью функции Ляпунова.
на устойчивость с помощью функции Ляпунова.
В качестве функции Ляпунова возьмём
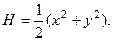
Она удовлетворяет обоим условиям: 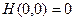 и
и 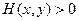 при
при 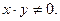 Её производная по времени равна
Её производная по времени равна
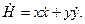
Значения 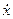 и
и 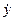 даны в условии задачи. Подставим их:
даны в условии задачи. Подставим их:
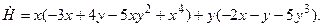
По условию нас интересует поведение ДС вблизи нуля (т.е. при 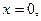
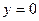 ). При малых значениях
). При малых значениях 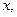
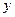 главную роль играют члены с наименьшими степенями. Их оставим, остальные отбросим:
главную роль играют члены с наименьшими степенями. Их оставим, остальные отбросим:
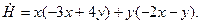
Отсюда
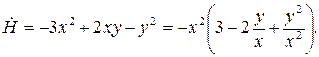
Это выражение можно преобразовать к виду
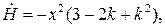 где
где 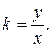
Выражение в скобках имеет дискриминант 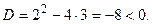 Это значит, что выражение в скобках всегда положительно. Следовательно,
Это значит, что выражение в скобках всегда положительно. Следовательно, 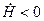 – нулевое решение асимптотически устойчиво. ■
– нулевое решение асимптотически устойчиво. ■
Дата: 2019-02-25, просмотров: 307.