Пусть эволюция ДС задаётся уравнением

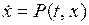                                      (6.1)

и начальным условием (входным данным)

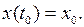                                      (6.2)

Решив задачу (6.1) – (6.2), получим частное решение

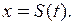                                  (6.3)

В (6.3) правая часть 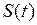 стала известной, поэтому выражение (6.3) отвечает на вопрос, как изменяется состояние ДС с течением времени. Обычно начальные данные не являются абсолютно точными, так как получаются путём измерений, а при измерении результат получается с некоторой погрешностью. А нам хотелось бы проследить, как сильно скажется неточность входных данных на точности конечного ответа.

Решение называют устойчивым, если бесконечно малое изменение начальных данных приводит к бесконечно малому изменению решения на протяжении всего дальнейшего времени 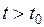 эволюции ДС.

Эту идею выразим формулами, пригодными для исследования уравнений, описывающих ДС.

Дано: динамическая система описывается уравнением 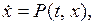которое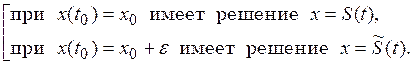

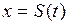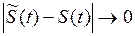Решение  называется: устойчивым, если  при 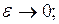асимптотически устойчивым, есл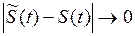и  при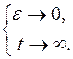

Если функция 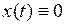 есть решение уравнения (6.1), то  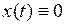называют нулевым решением уравнения.

Задачу об устойчивости решения ДУ (6.3) всегда можно свести к задаче об устойчивости нулевого решения. Поэтому достаточно разработать метод исследования на устойчивость нулевого решения ДУ.

В самом деле, предположим, что вы нашли функцию 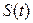 – решение уравнения (6.1). Это значит, что

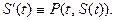                                                  (а)

В (6.1) сделаем замену 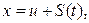 где 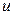 – новая неизвестная функция. Уравнение (6.1) примет вид

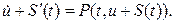                                     (б)

Вместо 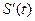 подставим его значение из (а)

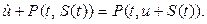
При 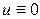 левая и правая части совпадают. Это означает, что нулевое решение  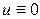есть решение уравнения (б).

З а д а ч а  1. Решение дифференциального уравнения

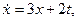                                                           (а)

с начальным условием

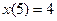
исследовать на устойчивость.

 Запишем ДУ в виде

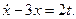                                                          (б)

Это линейное уравнение, поэтому общее решение имеет вид 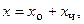 где 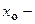 решение соответствующего однородного ДУ, а  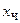– частное решение. Отбросим в (б) правую часть и для полученного однородного ДУ  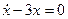составим характеристическое уравнение  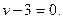Оно имеет корень  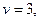поэтому  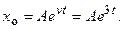Теперь учтём правую часть. Правая часть в (б) подсказывает, что частное решение следует искать в подобном же виде:  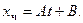Тогда 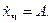 Подстановка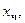 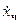 в (б) даёт  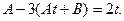Раскроем скобки:  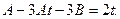Составим систему уравнений

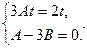
Отсюда находим 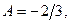 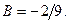Следовательно,  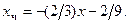Общее решение уравнения (б) выглядит так:

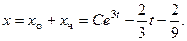
Запишем два одинаковых общих решения

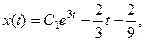                                                           (в)

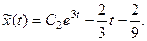                                    (г)

Для отыскания 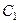 и 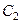 воспользуемся близкими друг другу начальными условиями

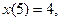
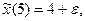                                                    (д)

где 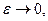 из-за чего будет выполняться условие  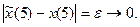Подставим значения (д) в (в) и (г). Получим равенства

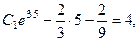
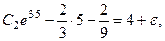
из которых находим 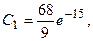 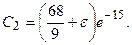Подставим их в (в), (г). Получим частные решения

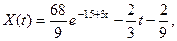                                               (д)

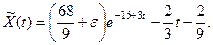
Тогда

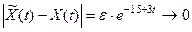 при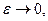

т.е. ДС устойчива. Однако если 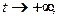 то 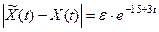 не стремится к нулю, а значит, ДС не является асимптотически устойчивой. ■