Пусть эволюция ДС задаётся автономным уравнением

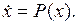
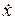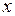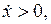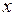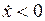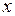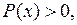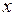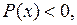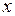Производная по времени  есть скорость изменения величины  – состояния ДС. Если  то  растёт с течением времени, а если , то  убывает. Или: если  то  с течением времени возрастает, если  то  убывает. Если же  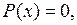то 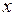 не уменьшается и не растёт, т.е. 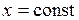– координата точки покоя ДС, или просто точка покоя.

Точка покоя (или неподвижная точка, особая точка, состояние равновесия) – точка, в которой скорость равна нулю.

Точки покоя одномерной ДС 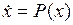есть корни уравнения

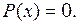
На рис. 8.1 график функции 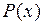 пересекает ось  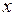в трёх точках 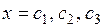. Они и есть точки покоя ДС, так как в них  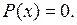Стрелки на оси  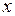показывают интервалы, где  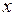растёт и где убывает. Состояния  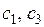устойчивы, а  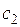неустойчиво.

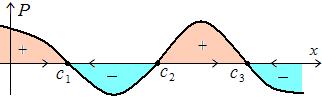
Рис. 8.1

В самом деле, пусть ДС находится в состоянии 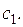 Если ДС немного отклонить от  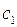в какую-либо сторону, то система будет стремиться вернуться в это состояние, как показывают стрелки, направленные к  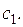А если ДС, находящуюся в состоянии  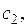немного отклонить от  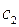в любую сторону, то ДС будет удаляться от этого состояния.

Таким образом, даже не решая исходное дифференциальное уравнение, можно исследовать поведение ДС. Характер поведения ДС уже виден на оси 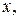 поэтому график функции P обычно не рисуют и оставляют лишь то, что происходит на оси 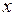(рис. 8.2):

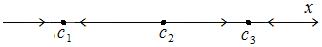
Рис. 8.2

Рис. 8.2 представляет пример фазового портрета ДС, в котором ось 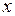 является фазовой прямой.

В любой точке покоя 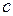 фазовый портрет одномерной ДС бывает одним из следующих четырёх типов (рис. 7.3):

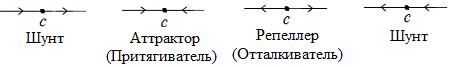
Рис. 8.3

З а д а ч а  1. Найти точки покоя и исследовать поведение ДС, описываемой уравнением

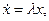
где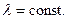

 Приравняем правую часть нулю: 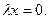 Отсюда  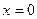– точка покоя. Если  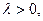то правая часть  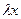на оси состояния  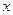имеет следующие знаки:

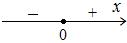
Поэтому фазовый портрет, изображающий поведение ДС, таков:

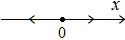
Видим, что состояние равновесия (точка покоя) неустойчиво (репеллер): при малейшем отклонении от точки 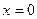 в ту или другую сторону система стремится удалиться от этой точки. Если же  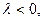то знаки на оси  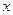поменяются:

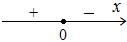
На фазовом портрете направление стрелок станет таким:

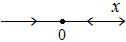
Здесь состояние равновесия устойчиво, является аттрактором: при малейшем отклонении от точки 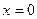 в ту или другую сторону система стремится вернуться в это состояние. ■

З а д а ч а  2. Найти состояния равновесия и исследовать поведение ДС, описываемой уравнением

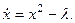
 Приравняем правую часть нулю, 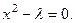 Отсюда  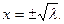Если 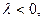 то уравнение не имеет вещественного решения, т.е. у ДС нет устойчивого состояния. Если  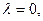то будем иметь единственную точку покоя  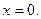Фазовый портрет ДС:

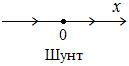
Если 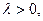 будем иметь две точки покоя  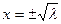и фазовый портрет ДС

 ■

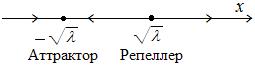З а д а ч а  3. Исследовать поведение ДС, описываемой уравнением

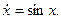
 Правая часть равна 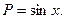 Её график и точки покоя показаны на рис. 8.4 а. На рис. 8.4 б дан фазовый портрет, дающий представление о поведении ДС вблизи точек покоя. Здесь мы видим, что аттракторы и репеллеры чередуются с промежутком между ними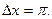

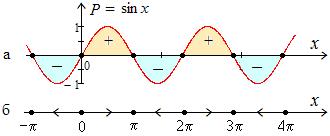
Рис. 8.4

Точки 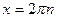 являются репеллерами (неустойчивыми точками покоя), а точки  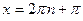– аттракторами (устойчивыми точками покоя)  ■

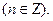З а д а ч а  4. Показать, что две ДС, описываемые уравнениям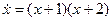и  и 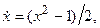 качественно эквивалентны.

 У первой ДС уравнение 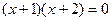даёт две точки покоя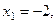 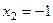. Поэтому эта ДС имеет фазовый портрет

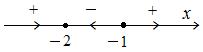
У второй ДС уравнение 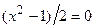 даёт тоже две точки покоя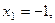 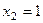. Поэтому вторая ДС имеет фазовый портрет

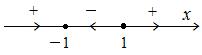
Фазовые портреты схожи, следовательно, обе ДС качественно эквивалентны. ■