ОБЩАЯ ТЕОРИЯ ДИНАМИЧЕСКИХ СИСТЕМ
Динамическая система
Динамическая система (ДС) – объект или процесс, состояние которого изменяется с течением времени.
Состояние механической системы – это координаты и скорости тел, входящих в систему.
Примеры динамических систем: физический маятник; электрический колебательный контур.
Если состояние ДС изменяется непрерывно, то ДС называют системой с непрерывным временем, или потоком.
Если состояние ДС изменяется скачком, дискретно, то ДС называют системой с дискретным временем, или каскадом.
Изменение состояния ДС с течением времени называют эволюцией ДС.
Вместо реальной ДС будем рассматривать её математическую модель.
Математическая модель динамической системы – это уравнение или система уравнений, описывающих эволюцию ДС.
Эволюция одномерной динамической системы
Обозначим 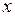 состояние ДС. Когда
состояние ДС. Когда 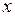 изменяется с течением времени, или зависит от времени, мы пишем
изменяется с течением времени, или зависит от времени, мы пишем 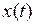 или
или 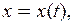 где
где 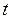 – время. В этом случае за бесконечно малый промежуток времени
– время. В этом случае за бесконечно малый промежуток времени 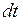 состояние изменится на бесконечно малую величину
состояние изменится на бесконечно малую величину 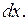 Поэтому скорость изменения состояния ДС равна
Поэтому скорость изменения состояния ДС равна 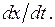 Эту скорость обозначим
Эту скорость обозначим 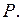 Если
Если 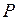 зависит от
зависит от 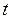 и от
и от 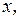 мы пишем
мы пишем 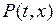 или
или 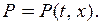 В результате получаем равенство
В результате получаем равенство
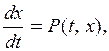
или
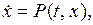 (2.1)
(2.1)
где точка над буквой есть другое обозначение производной по времени. Если функция 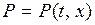 известна, то равенство (2.1) будет дифференциальным уравнением, содержащим неизвестную функцию
известна, то равенство (2.1) будет дифференциальным уравнением, содержащим неизвестную функцию 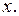 Решив уравнение (2.1), т.е. найдя функцию
Решив уравнение (2.1), т.е. найдя функцию 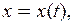 вы будете знать, как изменяется состояние ДС с течением времени. Уравнение (2.1) есть закон эволюции ДС.
вы будете знать, как изменяется состояние ДС с течением времени. Уравнение (2.1) есть закон эволюции ДС.
Общее и частное решения дифференциального уравнения
Чтобы решить уравнение (2.1), т.е. чтобы избавиться от знака производной и найти «чистое» 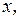 нужно выполнить обратное действие – интегрирование. Решение – результат вычисления неопределённого интеграла, всегда содержит произвольную постоянную величину, обычно обозначаемую буквой
нужно выполнить обратное действие – интегрирование. Решение – результат вычисления неопределённого интеграла, всегда содержит произвольную постоянную величину, обычно обозначаемую буквой 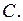 Поэтому пишут
Поэтому пишут 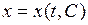 или просто
или просто 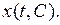
Решение, содержащее произвольную буквенную постоянную, называют общим решением.
Пример 3.1. Решив уравнение 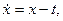 вы получите
вы получите 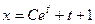 – общее решение (ибо в нём имеется произвольная постоянная
– общее решение (ибо в нём имеется произвольная постоянная 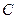 ).
).
Общее решение включает в себя бесчисленное множество решений.
Если 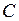 заменить каким-нибудь числом, получится частное решение.
заменить каким-нибудь числом, получится частное решение.
Пример 3.2. Возьмём общее решение из примера 1. Если вместо 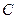 подставить 9, получится
подставить 9, получится 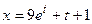 – частное решение.
– частное решение.
Интегральные линии
График частного решения на плоскости 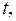
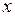 называют интегральной линией (рис. 4.1).
называют интегральной линией (рис. 4.1).
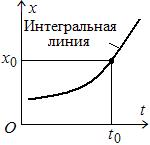 Подставляя в общее решение
Подставляя в общее решение 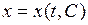 вместо
вместо 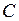 разные числа, будем получать различные частные решения и их графики. Эти графики, или по-другому, интегральные линии, заполнят собой некоторую область
разные числа, будем получать различные частные решения и их графики. Эти графики, или по-другому, интегральные линии, заполнят собой некоторую область 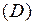 – область существования решений на плоскости
– область существования решений на плоскости 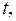
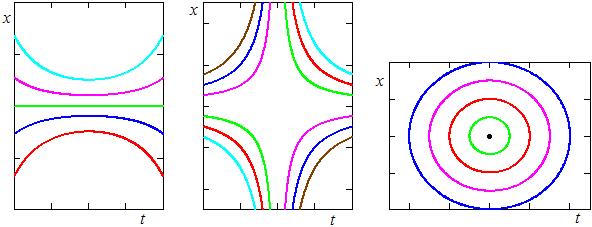
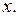 Примеры интегральных линий, полученных в результате решения некоторых уравнений, показаны на рис. 4.2.
Примеры интегральных линий, полученных в результате решения некоторых уравнений, показаны на рис. 4.2.
В реальной практике обычно известно начальное состояние ДС (или начальное условие): Рис. 4.1
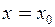 при
при 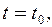
или
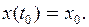
Пример 4.1. Если при 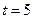 должно быть
должно быть 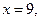 то это условие записывают в виде
то это условие записывают в виде 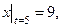 или
или 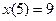 .
.
На плоскости 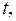
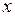 начальное условие изображается точкой с координатами
начальное условие изображается точкой с координатами 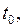
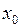 (рис. 4.1). Эта точка выделяет проходящую через неё интегральную линию.
(рис. 4.1). Эта точка выделяет проходящую через неё интегральную линию.
В общем случае возможно пересечение интегральных линий. Но если функция 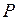 и её частная производная
и её частная производная 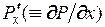 непрерывны в
непрерывны в 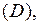 то интегральные линии пересекаться не могут.
то интегральные линии пересекаться не могут.
а б в
г д е
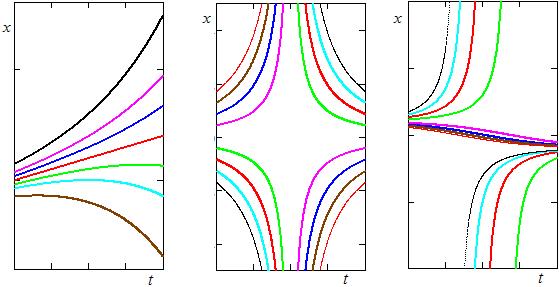
Рис. 4.2
Дифференциальных уравнений
Дифференциальное уравнение (ДУ) – равенство, содержащее производную или дифференциал неизвестной функции.
Поэтому цель решения ДУ – найти неизвестную функцию, избавившись от производной или дифференциала. Ещё раз отметим, что
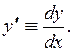
| ДУ 1 порядка | |
| Тип ДУ | Метод решения |
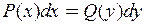 ДУ с отделёнными переменными
ДУ с отделёнными переменными
| 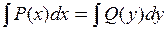
|
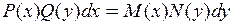 ДУ с отделяющимися переменными
ДУ с отделяющимися переменными
| Делим обе части на
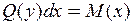
|
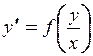 Однородное ДУ 1 порядка
Однородное ДУ 1 порядка
| 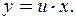 Тогда
Тогда 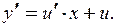 Подставляем и находим
Подставляем и находим 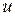
|
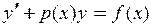 Линейное ДУ 1 порядка
Линейное ДУ 1 порядка
| 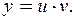
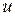 и и 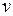 определяются из системы определяются из системы
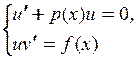
|
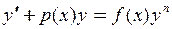 ДУ Бернулли
ДУ Бернулли
| 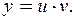
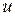 и и 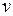 определяются из системы определяются из системы
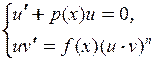
|
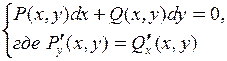 ДУ в полных дифференциалах
ДУ в полных дифференциалах
| 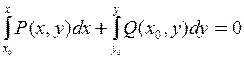
|
| ДУ 2 порядка | |
| Тип ДУ | Метод решения |
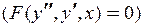 Неполное ДУ, нет
Неполное ДУ, нет 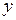
| Замена 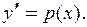 Тогда
Тогда 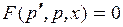
|
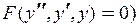 Неполное ДУ, нет
Неполное ДУ, нет 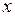
| Замена 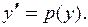 Тогда
Тогда 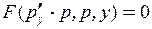
|
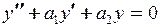 Линейное однородное ДУ 2 порядка с постоянными коэффициентами
Линейное однородное ДУ 2 порядка с постоянными коэффициентами
| Составим уравнение 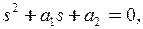 найдём
найдём 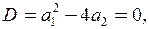 корни
корни 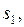 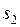 и пишем решение и пишем решение
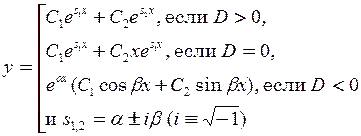
|
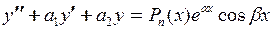 Линейное неоднородное ДУ 2 порядка с постоянными коэффициентами
Линейное неоднородное ДУ 2 порядка с постоянными коэффициентами
| Общее решение 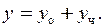 Здесь
Здесь 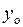 определяется из определяется из
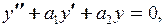 а
а 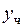 определяется подстановкой определяется подстановкой
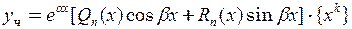 в исходное ДУ
в исходное ДУ
|
Фазовое пространство
Пусть эволюция двумерной ДС задаётся автономной системой ДУ
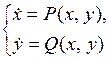 (9.1)
(9.1)
с известными правыми частями, не содержащими 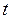 в явном виде. Решив эту систему, получим пару функций
в явном виде. Решив эту систему, получим пару функций
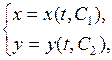 (9.2)
(9.2)
где 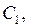
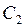 – постоянные. На плоскости введём систему координат
– постоянные. На плоскости введём систему координат 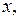
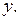 Решение (8.2) изобразится семейством линий.
Решение (8.2) изобразится семейством линий.
Фазовая плоскость – плоскость, на которой координаты 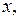
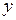 характеризуют состояние ДС.
характеризуют состояние ДС.
Фазовая точка – любая точка фазового пространства.
Фазовая линия (или фазовая траектория) – линия, по которой движется фазовая точка с течением времени.
Выражения (8.2) являются параметрическими уравнениями фазовой линии, если считать 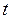 переменным параметром.
переменным параметром.
Фазовый портрет динамической системы – это набор фазовых линий.
Фазовый портрет системы (9.1) получается при различных начальных условиях. Для одномерной ДС фазовый портрет состоит из одной фазовой линии.
Точка покоя (или неподвижная точка, особая точка, состояние равновесия) – фазовая точка, скорость которой равна нулю.
Вектор 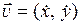 есть скорость фазовой точки. Если фазовая точка неподвижна, то
есть скорость фазовой точки. Если фазовая точка неподвижна, то 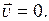 Равенство
Равенство 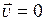 означает, что
означает, что
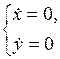 или
или 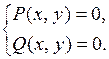
Значит,
Точки покоя двумерной ДС
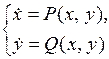 являются корнями системы двух уравнений
являются корнями системы двух уравнений
|
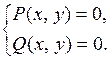
|
З а д а ч а 1. Найти точки покоя ДС, описываемой системой уравнений
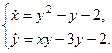
Приравняем правые части нулю:
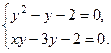
Из первого уравнения 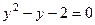 получаем
получаем 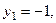
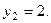 Второе уравнение запишем так:
Второе уравнение запишем так: 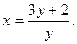 Подстановка значений
Подстановка значений 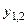 даст соответственно
даст соответственно 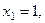
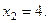 Следовательно, на фазовой плоскости
Следовательно, на фазовой плоскости 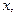
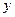 точками покоя являются две точки с координатами
точками покоя являются две точки с координатами 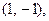
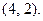 ■
■
По первому приближению
Дано: динамическая система описывается системой уравнений
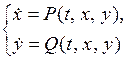 и
и 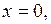 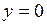 – нулевое решение этой системы. – нулевое решение этой системы.
|
Составляем характеристическое уравнение
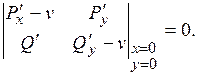 (10.1)
Находим его корни (10.1)
Находим его корни 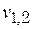 и их вещественные части и их вещественные части 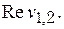 Делаем вывод:
нулевое решение:
- асимптотически устойчиво, если все Делаем вывод:
нулевое решение:
- асимптотически устойчиво, если все 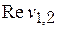 отрицательны;
- неустойчиво, если среди отрицательны;
- неустойчиво, если среди 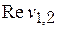 имеется положительное число;
- нужно исследовать другим способом, если среди имеется положительное число;
- нужно исследовать другим способом, если среди 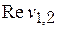 имеется ноль
(критический случай). имеется ноль
(критический случай).
|
З а д а ч а 1. Динамическая система описывается системой уравнений
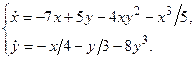
Исследовать точку покоя 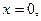
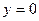 на устойчивость по первому приближению.
на устойчивость по первому приближению.
Выпишем правые части:
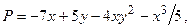
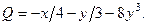
Найдём их частные производные:
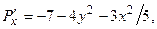
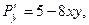
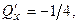
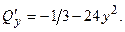
Составим характеристическое уравнение
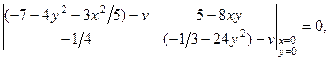 или
или 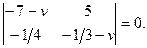
Раскроем определитель
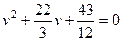 или
или 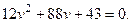
Вычислим корни
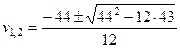 .
.
Оба корня вещественны и отрицательны. Следовательно, точка покоя асимптотически устойчива. ■
С помощью функции Ляпунова
Дано: динамическая система описывается системой уравнений
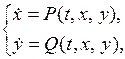
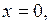 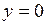 – нулевое решение этой системы, – нулевое решение этой системы,
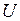 – окрестность начала координат. – окрестность начала координат.
|
Если существует вещественная функция 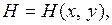 удовлетворяющая условиям
удовлетворяющая условиям
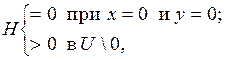 то нулевое решение:
при
то нулевое решение:
при  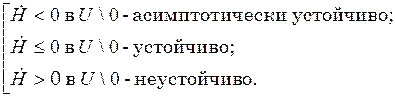
|
Окрестность точки – это какая-либо область, содержащая эту точку. Здесь 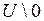 – область, не содержащая начало координат.
– область, не содержащая начало координат.
Функция 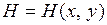 называется функцией Ляпунова.
называется функцией Ляпунова.
З а д а ч а 1. Динамическая система описывается системой уравнений
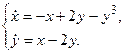
Исследовать нулевое решение 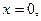
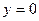 на устойчивость с помощью функции Ляпунова.
на устойчивость с помощью функции Ляпунова.
В качестве функции Ляпунова возьмём
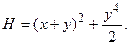
Она удовлетворяет обоим условиям: 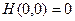 и
и 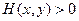 при
при 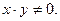 Её производная по времени равна
Её производная по времени равна
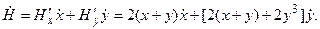
Значения 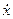 и
и 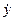 даны в условии задачи. Подставим их:
даны в условии задачи. Подставим их:
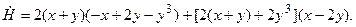
После упрощений получим 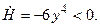 Это значит, что нулевое решение
Это значит, что нулевое решение 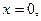
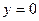 асимптотически устойчиво. ■
асимптотически устойчиво. ■
З а д а ч а 2. Динамическая система описывается системой уравнений
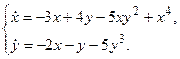
Исследовать нулевое решение 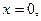
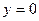 на устойчивость с помощью функции Ляпунова.
на устойчивость с помощью функции Ляпунова.
В качестве функции Ляпунова возьмём
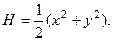
Она удовлетворяет обоим условиям: 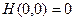 и
и 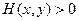 при
при 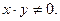 Её производная по времени равна
Её производная по времени равна
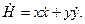
Значения 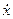 и
и 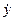 даны в условии задачи. Подставим их:
даны в условии задачи. Подставим их:
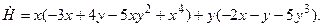
По условию нас интересует поведение ДС вблизи нуля (т.е. при 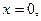
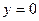 ). При малых значениях
). При малых значениях 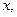
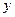 главную роль играют члены с наименьшими степенями. Их оставим, остальные отбросим:
главную роль играют члены с наименьшими степенями. Их оставим, остальные отбросим:
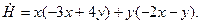
Отсюда
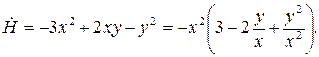
Это выражение можно преобразовать к виду
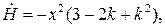 где
где 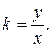
Выражение в скобках имеет дискриминант 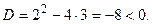 Это значит, что выражение в скобках всегда положительно. Следовательно,
Это значит, что выражение в скобках всегда положительно. Следовательно, 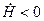 – нулевое решение асимптотически устойчиво. ■
– нулевое решение асимптотически устойчиво. ■
Динамической системы
Рассмотрим ДС, которая описывается системой ДУ вида
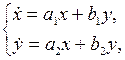 (13.1)
(13.1)
где 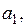
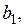
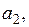
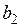 – константы. Для этой системы начало координат
– константы. Для этой системы начало координат 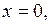
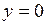 является точкой покоя. Исследуем эту точку на устойчивость по первому приближению. Имеем
является точкой покоя. Исследуем эту точку на устойчивость по первому приближению. Имеем
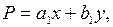
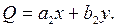
Отсюда:
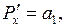
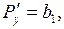
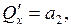
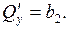
Составим характеристическое уравнение по формуле (10.1):
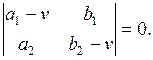
Раскрыв определитель, получим квадратное уравнение
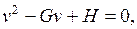
где 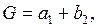
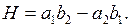 Находим два его корня
Находим два его корня
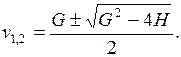
Возможны следующие случаи. Таблица (13.2)
| 1. Корни | ||||
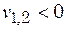
| 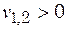
| 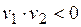
| 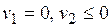
| 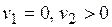
|
| В этом случае точка покоя: | ||||
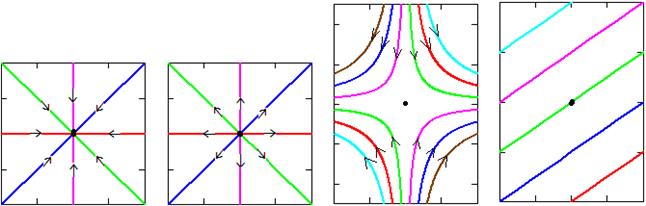
| асимптотически устойчивый узел (рис. 13.1 а) | неустойчивый узел (рис. 13.1 б) | седло, неустойчива (рис. 13.1 в) | устойчива (рис. 13.1 г) | неустойчива |
| 2. Корни | ||
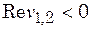
| 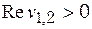
| 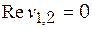
|
| В этом случае точка покоя: | ||
| асимптотически устойчивый фокус, колебания затухают (рис. 13.1 д) | Неустойчивый фокус, колебания нарастают (рис. 13.1 е) | устойчивый центр, незатухающие автоколебания (рис. 13.1 ё) |
На рис. 13.1 показаны варианты поведения фазовых линий (или поведения динамической системы) вблизи точки покоя.
а б в г
 д е ё
д е ё
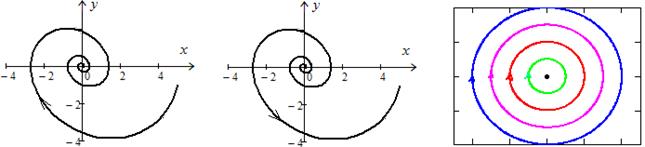
Рис. 13.1
З а д а ч а 1. Определить характер точки покоя динамической системы, заданной системой ДУ
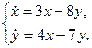
Приравняем правые части нулю,
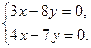
Из этой системы уравнений находим 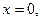
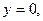 т.е. начало координат
т.е. начало координат 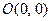 является точкой покоя. Составим характеристическое уравнение по формуле (10.1):
является точкой покоя. Составим характеристическое уравнение по формуле (10.1):
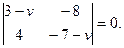
Раскрыв определитель, получим квадратное уравнение
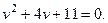
Его корни:
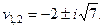
Корни получились комплексные и 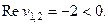 Поэтому в соответствии с таблицей (13.2) получаем ответ: точка покоя
Поэтому в соответствии с таблицей (13.2) получаем ответ: точка покоя 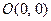 является устойчивым фокусом. ■
является устойчивым фокусом. ■
Автоколебательные системы
ДС, в которой все фазовые траектории притягиваются к замкнутой траектории, называется автоколебательной. Автоколебательной ДС может быть только нелинейная диссипативная (в которой энергия рассеивается из-за трения) система. Замкнутая траектория в фазовом пространстве, соответствующая периодическому движению, называется предельным циклом Пуанкаре.
В качестве примера ДС с предельным циклом Пуанкаре рассмотрим электрический контур с нелинейным сопротивлением 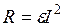 и с подкачкой энергии извне, равной
и с подкачкой энергии извне, равной 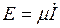
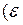 и
и 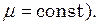 Уравнение (16.6) примет вид
Уравнение (16.6) примет вид
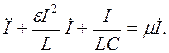
или
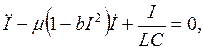
где обозначено 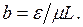 После замены
После замены 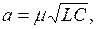
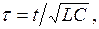
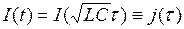 получим уравнение
получим уравнение
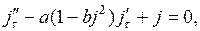 (17.1)
(17.1)
называемое уравнением Ван дер Поля. Введя обозначения 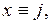
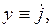 запишем (17.1) в фазовых координатах
запишем (17.1) в фазовых координатах
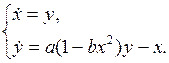
На рис. 17.1 и 17.2 показаны фазовые траектории при 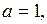
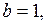 которые притягиваются к одному и тому же предельному циклу. Рис. 17.1 построен при начальных условиях
которые притягиваются к одному и тому же предельному циклу. Рис. 17.1 построен при начальных условиях 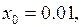
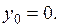 Здесь фазовая точка, находясь в начальный момент внутри предельного цикла, через какое-то время попадает на предельный цикл и в дальнейшем его не покидает.
Здесь фазовая точка, находясь в начальный момент внутри предельного цикла, через какое-то время попадает на предельный цикл и в дальнейшем его не покидает.
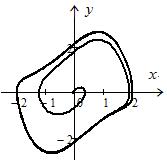
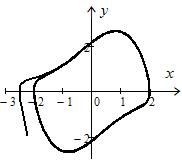
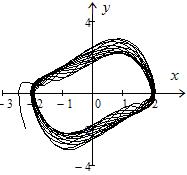
Рис. 17.1 Рис. 17.2 Рис. 17.3
Рис. 17.2 построен при начальных условиях 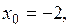
 Здесь фазовая точка, находясь в начальный момент вне предельного цикла, через какое-то время попадает на предельный цикл и в дальнейшем его не покидает. Таким образом, к предельному циклу притягиваются все фазовые точки из любого начального положения.
Здесь фазовая точка, находясь в начальный момент вне предельного цикла, через какое-то время попадает на предельный цикл и в дальнейшем его не покидает. Таким образом, к предельному циклу притягиваются все фазовые точки из любого начального положения.
Добавим в правую часть уравнения (17.1) периодическое возмущение малой амплитуды 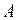 и частоты
и частоты 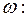
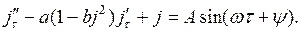
Фазовая точка с частотой 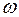 будет вращаться вокруг предельного цикла (рис. 17.3, где
будет вращаться вокруг предельного цикла (рис. 17.3, где 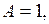
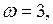
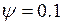 ).
).
Бифуркации ДС
Бифуркация – потеря первоначальной устойчивости и переход ДС в другое устойчивое состояние.
Вернёмся к рассмотрению уравнения (16.7) колебаний тока в колебательном контуре:
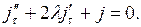
Параметр 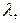 зависящий от сопротивления в контуре, влияет на характер колебаний. При
зависящий от сопротивления в контуре, влияет на характер колебаний. При 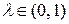 амплитуда колебаний экспоненциально убывает (рис. 18.1, где
амплитуда колебаний экспоненциально убывает (рис. 18.1, где 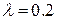 ). При
). При 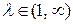 колебаний уже не будет (рис. 18.2, где
колебаний уже не будет (рис. 18.2, где 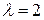 ). В этом случае говорят, что движение апериодическое.
). В этом случае говорят, что движение апериодическое.
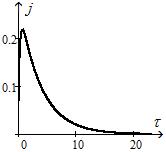
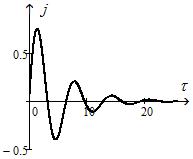
Рис. 18.1 Рис. 18.2
Таким образом, при переходе параметра 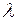 через значение
через значение 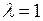 характер изменения тока во времени существенно различается.
характер изменения тока во времени существенно различается.
Значение параметра, при котором поведение ДС качественно меняется (в данном случае это значение 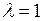 ), называется точкой бифуркации (бифуркация означает раздвоение, расщепление).
), называется точкой бифуркации (бифуркация означает раздвоение, расщепление).
Если в ДС параметр не переходит через точку бифуркации, то ДС называется грубой. Если же в ДС происходит переход параметра через точку бифуркации, то ДС является негрубой. В этом случае, когда параметр находится вблизи точки бифуркации, малое изменение параметра может привести к резкому изменению состояния ДС.
Пример. Пусть ДС задана уравнением
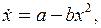 где
где 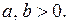 (18.1)
(18.1)
В стационарном состоянии (т.е. когда состояние не меняется во времени) 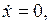 и мы получим
и мы получим 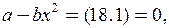
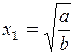 и
и 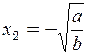
– два стационарных состояния.
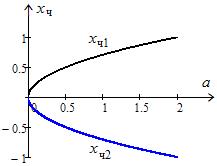
Зафиксируем 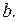 Зависимости
Зависимости 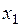 и
и 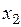 от
от 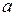 изобразятся в виде двух ветвей параболы (рис. 18.3, где взято
изобразятся в виде двух ветвей параболы (рис. 18.3, где взято 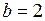 ). Значение
). Значение 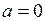 есть точка бифуркации. Если чуть увеличить
есть точка бифуркации. Если чуть увеличить 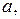 ДС перейдёт в одно из двух состояний
ДС перейдёт в одно из двух состояний 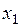 или
или 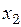 и будет постоянно в нём находиться, пока
и будет постоянно в нём находиться, пока 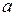 остаётся вдали от значения
остаётся вдали от значения 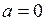 . При
. При
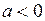 стационарные состояния исчезают. Рис. 18.3
стационарные состояния исчезают. Рис. 18.3
Качественный анализ ДС
Пусть состояние ДС задаётся единственной величиной (координатой) 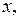 зависящей от времени, а эволюция – уравнением
зависящей от времени, а эволюция – уравнением
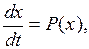
или
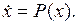
Вы знаете, что при 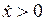 величина
величина 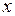 растёт с течением времени, а при
растёт с течением времени, а при 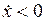 убывает. Значит, если
убывает. Значит, если 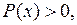 то
то 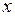 с течением времени возрастает, если
с течением времени возрастает, если 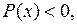 то
то 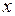 убывает, а если
убывает, а если 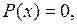 то величина
то величина 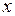 не уменьшается и не растёт, т.е. постоянна,
не уменьшается и не растёт, т.е. постоянна, 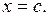
Состояние 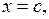 где
где 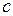 – корень уравнения
– корень уравнения 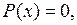 называется состоянием (или точкой) равновесия.
называется состоянием (или точкой) равновесия.
На рис. 8.1 показан случай, когда уравнение 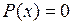 имеет три корня
имеет три корня 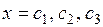 – три состояния равновесия. Стрелки на оси
– три состояния равновесия. Стрелки на оси 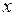 показывают интервалы, места, где
показывают интервалы, места, где 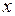 растёт и где убывает. Здесь мы видим, что состояния
растёт и где убывает. Здесь мы видим, что состояния 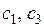 устойчивы, а
устойчивы, а 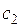 неустойчиво.
неустойчиво.
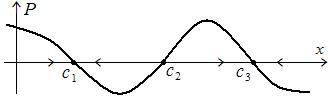
Рис. 8.1
Таким образом, даже не решая исходное дифференциальное уравнение можно исследовать поведение ДС. Характер поведения ДС показан на оси 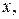 поэтому график функции P обычно не рисуют и оставляют лишь то, что происходит на оси
поэтому график функции P обычно не рисуют и оставляют лишь то, что происходит на оси 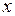 (рис. 8.2):
(рис. 8.2):
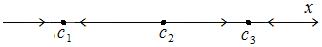
Рис. 8.2
Такое изображение поведения ДС называется фазовым портретом ДС, а ось 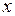 – фазовой прямой.
– фазовой прямой.
Для ДС с единственным состоянием равновесия 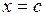 фазовый портрет бывает одним из следующих четырёх типов (рис. 8.3):
фазовый портрет бывает одним из следующих четырёх типов (рис. 8.3):
а б в г
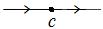
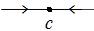
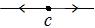
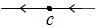
Рис. 8.3
Состояние 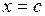 в случаях (а), (г) называется шунтом, в случае (б) аттрактором (притягивателем), в случае (в) репеллером (отталкивателем).
в случаях (а), (г) называется шунтом, в случае (б) аттрактором (притягивателем), в случае (в) репеллером (отталкивателем).
З а д а ч а 1. Найти состояние равновесия и исследовать поведение ДС, описываемой уравнением
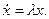
Приравняем правую часть нулю: 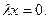 Отсюда
Отсюда 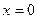 – состояние равновесия. Если
– состояние равновесия. Если 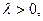 то правая часть
то правая часть 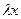 на оси состояния
на оси состояния 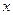 имеет следующие знаки:
имеет следующие знаки:
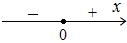
Поэтому фазовый портрет, на котором изображается поведение ДС, таков:
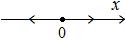
Видим, что состояние равновесия неустойчиво (репеллер): при малейшем отклонении от точки 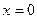 в ту или другую сторону система стремится удалиться от этого состояния.
в ту или другую сторону система стремится удалиться от этого состояния.
Если же 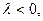 то знаки на оси
то знаки на оси 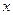 поменяются:
поменяются:
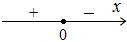
На фазовом портрете направление стрелок станет таким:
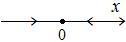
Здесь состояние равновесия устойчиво (аттрактор): при малейшем отклонении от точки 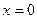 в ту или другую сторону система стремится вернуться в это состояние. ■
в ту или другую сторону система стремится вернуться в это состояние. ■
З а д а ч а 2. Найти состояния равновесия и исследовать поведение ДС, описываемой уравнением
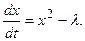
Приравняем правую часть нулю, 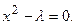 Отсюда
Отсюда 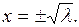 Если
Если 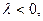 то уравнение не имеет вещественного решения, т.е. у ДС нет устойчивого состояния. Если
то уравнение не имеет вещественного решения, т.е. у ДС нет устойчивого состояния. Если 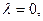 то уравнение имеет единственное решение
то уравнение имеет единственное решение 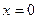 и фазовый портрет
и фазовый портрет
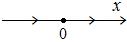
Состояние равновесия является шунтом. Наконец, если 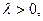 то уравнение имеет два решения
то уравнение имеет два решения 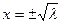 и фазовый портрет
и фазовый портрет
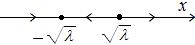
Из него видим, что состояние равновесия 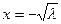 является аттрактором (т.е. устойчивым), состояние
является аттрактором (т.е. устойчивым), состояние 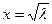 репеллером (неустойчивым). ■
репеллером (неустойчивым). ■
Пусть состояние ДС задаётся двумя величинами (координатами) 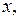
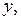 зависящими времени, а эволюция ДС – системой уравнений
зависящими времени, а эволюция ДС – системой уравнений
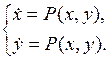
Поведение ДС теперь изображается на плоскости состояний 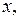
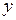 – фазовой плоскости. Как и в предыдущем случае, состояния (точки) равновесия ДС определяются из условий
– фазовой плоскости. Как и в предыдущем случае, состояния (точки) равновесия ДС определяются из условий
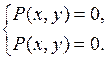
Рассмотрим систему
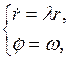
в которой 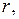
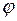 – полярные координаты, связанные с декартовыми по формулам
– полярные координаты, связанные с декартовыми по формулам 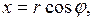
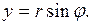 Смысл полярных координат:
Смысл полярных координат: 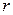 – расстояние от начала координат,
– расстояние от начала координат, 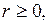 а
а 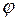 – угол, отсчитываемый от положительного направления оси
– угол, отсчитываемый от положительного направления оси 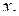 Поэтому
Поэтому 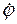 – угловая скорость. В рассматриваемой ДС точкой равновесия является
– угловая скорость. В рассматриваемой ДС точкой равновесия является 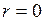 – начало координат О. Если
– начало координат О. Если 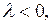 то
то 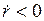 – закручивающиеся вокруг О спирали, поэтому О называют устойчивым фокусом. Если
– закручивающиеся вокруг О спирали, поэтому О называют устойчивым фокусом. Если 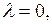 то
то 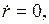 отсюда
отсюда 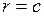 – окружности различных радиусов
– окружности различных радиусов 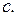 Если
Если 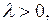 то
то 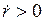 и поэтому О является неустойчивым фокусом. Следовательно, ДС испытывает бифуркацию при
и поэтому О является неустойчивым фокусом. Следовательно, ДС испытывает бифуркацию при 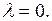 Фазовые линии при
Фазовые линии при 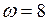 для случаев
для случаев 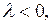
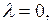
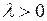 показаны на рис. 8.4.
показаны на рис. 8.4.
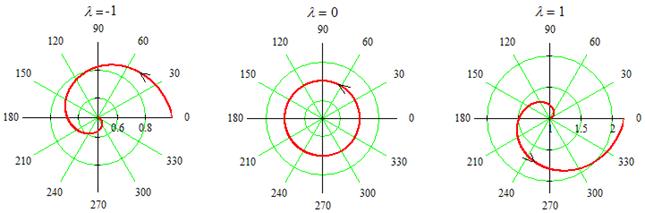
Рис. 8.4
Рассмотрим систему
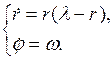
Приравняв правую часть первого уравнения к нулю, 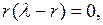 найдём два равновесных состояния
найдём два равновесных состояния 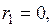
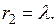
Практические задания по дисциплине
«Общая теория динамических систем»
Раздел 1. Дополнительные сведения об обыкновенных дифференциальных уравнениях. (ОК-1, ПК-5)
Практическое занятие 1. Системы обыкновенных дифференциальных уравнений. Основные свойства. Фазовые траектории.
1. Найти общее решение системы уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.
x'(t) = 2x + y
y'(t) = 4x-y
2. Найти положения равновесия, определить их характер и нарисовать фазовые траектории линеаризованных систем в окрестности положения равновесия для автономной системы уравнений
х'(t) = y2-y-2
у '(t)=-ху-3у-2
Практическое занятие 2. Линейные системы дифференциальных уравнений. Различные способы решения. Операторный способ решения систем с постоянными коэффициентами.
1. Найти решение уравнения операционным методом, удовлетворяющее начальным условиям.
x'' + 4х' + 3x = e-3t cost
х(0) = 1, х'(0) = 0
2. Найти решение уравнения, удовлетворяющее начальным условиям
x(0) = 1, х'(0) = 1 х''-4х' + 3х = t2.
Раздел 2. Элементы качественной теории дифференциальных уравнений (ПК-2, ПК-5)
Практическое занятие 1. Устойчивость системы. Линеаризация уравнений. Устойчивость по Ляпунову.
1. Найти общее решение систем уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.
x'(t) = -x+8y
у'(t) = х+у
2. Найти положения равновесия, определить их характер и нарисовать фазовые траекторий линеаризованных систем в окрестности положения равновесия для автономных систем
x'(t) = x2+x+2y2 - 2
y'(t)=x + y2
Практическое занятие 2. Особые точки систем. Классификация особых точек
7. Найти общее решение систем уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.
x'(t) = x-y
y'(t) = y-4x
8. Найти положения равновесия, определить их характер и нарисовать фазовые траектории линеаризованных систем в окрестности положения равновесия для автономных систем
x'(t) = y2-y-2
y'(t) = -xy-3y-2
Практическое занятие 3. Поведение фазовых траекторий в окрестностях грубых положений равновесия
9. Опишите бифуркацию в динамической системе, описываемой системой уравнений
x'1=-x21+ε, x'2=-x2.
10. Найти общее решение систем уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.
x'(t) =2x+y
y'(t) =3х+4у
Практическое занятие 4. Дифференциальные уравнения зависящие от параметра. Фазовые портреты узлов, седла и фокуса
11. Найти положения равновесия, определить их характер и нарисовать фазовые траектории линеаризованных систем в окрестности положения равновесия для автономных систем
x'(t) =1-2x-y2
y'(t) =e-4x-1
12. Исследовать устойчивость неподвижных точек одномерного отображения при различных значениях параметров системы. Действие отображения изобразить с помощью диаграммы Ламерея. Найдите бифуркационное значения параметра и изобразите диаграммы.
хn+1=λ.хn-хn3
Практическое занятие 5. Предельные циклы. Полуустойчивый цикл. Бифуркации рождения циклов, Гомоклинические траектории. Седло-узел. Бифуркация рождения предельного цикла, когда исчезает гомоклиническая траектория.
13. Найти решение уравнения, удовлетворяющее начальным условиям
х(0) = 1, х'(0) = l, x''+x = tsint
14. Найти общее решение систем уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.
х'(t) = x-5y
у'(t) = 2x-y
Практическое занятие 6. Рождение устойчивого предельного цикла, когда существует гомоклиническая траектория, выходящая из седла.
1. Найти положения равновесия, определить их характер и нарисовать фазовые траектории линеаризованных систем в окрестности положения равновесия для автономных систем
х(t) = x-2y-y2
2. Найти общее решение системы уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.
x'(t) = x + 2y
y'(t) = 4x+3y
Практическое занятие 7. Одномерные отображения. Диаграмма Ламерея. Отображения сдвига. Отображения сжатия. Отображение сжатия плюс сдвиг.
Исследовать устойчивость неподвижных точек одномерного отображения при различных значениях параметров системы. Действие отображения изобразить с помощью диаграммы Ламерея. Найдите бифуркационное значения параметра и изобразите диаграммы.
хn+1=λ.хn-хn3
Опишите бифуркацию в динамической системе, описываемой уравнением х' = -х2 + ε
Раздел 3. Теория линейных динамических систем (ОК-1, ОК-2, ПК-2, ПК-4)
Практическое занятие 1. Линейные управляемые динамические системы в дискретной и непрерывной форме. Фазовые траектории управляемых систем.
Найти решение уравнения, удовлетворяющее начальным условиям
х(0) = 1, х(0) = 1 x''-4x' + 5x = e4t
2. Найти общее решение системы уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.
x'(t) = 2x + y
y'(t)=4x-y
Практическое занятие 2. Пространства состояний, входов и выходов динамической системы. Операторы переходов, входов и выходов динамических систем. Представление в явной форме или в виде уравнений. Примеры.
Найти положения равновесия, определить их характер и нарисовать фазовые траектории линеаризованных систем в окрестности положения равновесия для автономной системы.
х'(t) = у2-у-2
y'(t) = -xy-3y-2
2. Найти решение уравнения операционным методом удовлетворяющее начальным условиям.
х+4х + 3х = е-3t cost
х(0) = 1, х'(0) = 0
Практическое занятие 3. Математические модели процессов и систем.
Найти общее решение системы уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.
x'(t)=x-5y
y'(t)=2x-y
2. Опишите бифуркацию в динамической системе, описываемой в полярных координатах уравнением ρ'=(ε-ρ2+2ρ-1), φ=1.
Практическое занятие 4. Линейные стационарные системы. Условия наблюдаемости и управляемости.
Найти общее решение системы уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.
х'(t) = x + 2y
y'(t) = 4x+3y
Найти решение уравнения, удовлетворяющее начальным условиям
х(0) = 1, х'(0) = l x''-4x' + 3x = t2
Список литературы
· Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах М.: ОНИКС 21 век, 2002.
· Берман Г.Н. Сборник задач по курсу математического анализа. СПб: Профессия, 2003.
· Кремер Н.Ш. Практикум по высшей математике. М.: ЮНИТИ-ДАНА, 2003.
· Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А. Сборник задач по высшей математике. 2 курс. М.: Айрис-пресс, 2004.
· Минорский В.П. Сборник задач по высшей математике.(Учебное пособие для студентов ВТУЗов).М.,»Наука»,1987г.
· Кудрявцев В.А. , Демидович Б.П. Краткий курс высшей математики (Учебное пособие для вузов). М., «Астрель.АСТ» 2007.
· Щипачев В.С. Основы высшей математики. (Учебное пособие для втузов). М., «Высшая школа»,1994.
ОБЩАЯ ТЕОРИЯ ДИНАМИЧЕСКИХ СИСТЕМ
Динамическая система
Динамическая система (ДС) – объект или процесс, состояние которого изменяется с течением времени.
Состояние механической системы – это координаты и скорости тел, входящих в систему.
Примеры динамических систем: физический маятник; электрический колебательный контур.
Если состояние ДС изменяется непрерывно, то ДС называют системой с непрерывным временем, или потоком.
Если состояние ДС изменяется скачком, дискретно, то ДС называют системой с дискретным временем, или каскадом.
Изменение состояния ДС с течением времени называют эволюцией ДС.
Вместо реальной ДС будем рассматривать её математическую модель.
Математическая модель динамической системы – это уравнение или система уравнений, описывающих эволюцию ДС.
Дата: 2019-02-25, просмотров: 414.
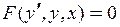
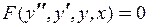
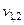 вещественные
вещественные 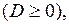
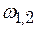 комплексные
комплексные