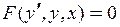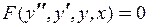Обозначим 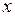 состояние ДС. Когда
состояние ДС. Когда 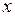 изменяется с течением времени, или зависит от времени, мы пишем
изменяется с течением времени, или зависит от времени, мы пишем 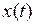 или
или 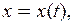 где
где 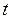 – время. В этом случае за бесконечно малый промежуток времени
– время. В этом случае за бесконечно малый промежуток времени 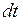 состояние изменится на бесконечно малую величину
состояние изменится на бесконечно малую величину 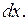 Поэтому скорость изменения состояния ДС равна
Поэтому скорость изменения состояния ДС равна 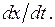 Эту скорость обозначим
Эту скорость обозначим 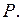 Если
Если 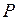 зависит от
зависит от 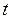 и от
и от 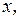 мы пишем
мы пишем 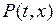 или
или 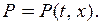 В результате получаем равенство
В результате получаем равенство
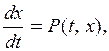
или
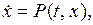 (2.1)
(2.1)
где точка над буквой есть другое обозначение производной по времени. Если функция 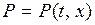 известна, то равенство (2.1) будет дифференциальным уравнением, содержащим неизвестную функцию
известна, то равенство (2.1) будет дифференциальным уравнением, содержащим неизвестную функцию 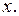 Решив уравнение (2.1), т.е. найдя функцию
Решив уравнение (2.1), т.е. найдя функцию 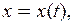 вы будете знать, как изменяется состояние ДС с течением времени. Уравнение (2.1) есть закон эволюции ДС.
вы будете знать, как изменяется состояние ДС с течением времени. Уравнение (2.1) есть закон эволюции ДС.
Общее и частное решения дифференциального уравнения
Чтобы решить уравнение (2.1), т.е. чтобы избавиться от знака производной и найти «чистое» 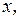 нужно выполнить обратное действие – интегрирование. Решение – результат вычисления неопределённого интеграла, всегда содержит произвольную постоянную величину, обычно обозначаемую буквой
нужно выполнить обратное действие – интегрирование. Решение – результат вычисления неопределённого интеграла, всегда содержит произвольную постоянную величину, обычно обозначаемую буквой 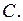 Поэтому пишут
Поэтому пишут 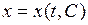 или просто
или просто 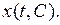
Решение, содержащее произвольную буквенную постоянную, называют общим решением.
Пример 3.1. Решив уравнение 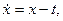 вы получите
вы получите 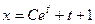 – общее решение (ибо в нём имеется произвольная постоянная
– общее решение (ибо в нём имеется произвольная постоянная 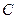 ).
).
Общее решение включает в себя бесчисленное множество решений.
Если 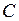 заменить каким-нибудь числом, получится частное решение.
заменить каким-нибудь числом, получится частное решение.
Пример 3.2. Возьмём общее решение из примера 1. Если вместо 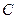 подставить 9, получится
подставить 9, получится 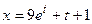 – частное решение.
– частное решение.
Интегральные линии
График частного решения на плоскости 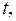
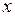 называют интегральной линией (рис. 4.1).
называют интегральной линией (рис. 4.1).
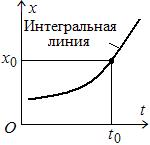 Подставляя в общее решение
Подставляя в общее решение 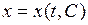 вместо
вместо 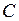 разные числа, будем получать различные частные решения и их графики. Эти графики, или по-другому, интегральные линии, заполнят собой некоторую область
разные числа, будем получать различные частные решения и их графики. Эти графики, или по-другому, интегральные линии, заполнят собой некоторую область 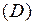 – область существования решений на плоскости
– область существования решений на плоскости 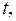
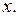 Примеры интегральных линий, полученных в результате решения некоторых уравнений, показаны на рис. 4.2.
Примеры интегральных линий, полученных в результате решения некоторых уравнений, показаны на рис. 4.2.
В реальной практике обычно известно начальное состояние ДС (или начальное условие): Рис. 4.1
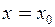 при
при 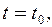
или
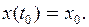
Пример 4.1. Если при 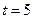 должно быть
должно быть 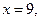 то это условие записывают в виде
то это условие записывают в виде 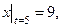 или
или 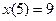 .
.
На плоскости 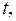
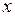 начальное условие изображается точкой с координатами
начальное условие изображается точкой с координатами 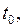
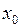 (рис. 4.1). Эта точка выделяет проходящую через неё интегральную линию.
(рис. 4.1). Эта точка выделяет проходящую через неё интегральную линию.
В общем случае возможно пересечение интегральных линий. Но если функция 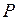 и её частная производная
и её частная производная 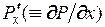 непрерывны в
непрерывны в 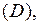 то интегральные линии пересекаться не могут.
то интегральные линии пересекаться не могут.
а б в
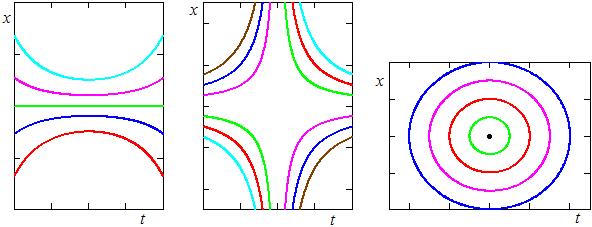
г д е
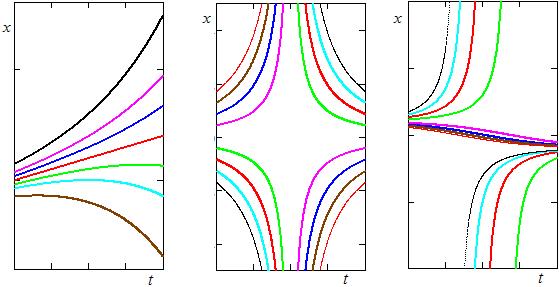
Рис. 4.2
Сводка методов решения специальных типов
Дифференциальных уравнений
Дифференциальное уравнение (ДУ) – равенство, содержащее производную или дифференциал неизвестной функции.
Поэтому цель решения ДУ – найти неизвестную функцию, избавившись от производной или дифференциала. Ещё раз отметим, что
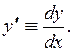
| ДУ 1 порядка | |
| Тип ДУ | Метод решения |
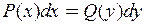 ДУ с отделёнными переменными
ДУ с отделёнными переменными
| 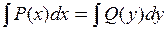
|
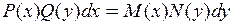 ДУ с отделяющимися переменными
ДУ с отделяющимися переменными
| Делим обе части на
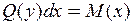
|
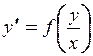 Однородное ДУ 1 порядка
Однородное ДУ 1 порядка
| 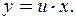 Тогда
Тогда 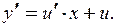 Подставляем и находим
Подставляем и находим 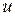
|
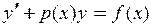 Линейное ДУ 1 порядка
Линейное ДУ 1 порядка
| 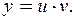
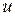 и и 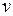 определяются из системы определяются из системы
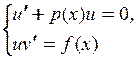
|
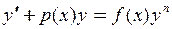 ДУ Бернулли
ДУ Бернулли
| 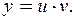
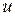 и и 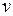 определяются из системы определяются из системы
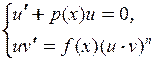
|
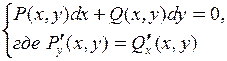 ДУ в полных дифференциалах
ДУ в полных дифференциалах
| 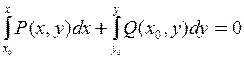
|
| ДУ 2 порядка | |
| Тип ДУ | Метод решения |
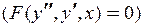 Неполное ДУ, нет
Неполное ДУ, нет 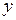
| Замена 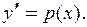 Тогда
Тогда 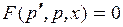
|
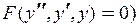 Неполное ДУ, нет
Неполное ДУ, нет 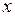
| Замена 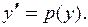 Тогда
Тогда 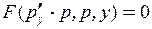
|
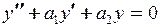 Линейное однородное ДУ 2 порядка с постоянными коэффициентами
Линейное однородное ДУ 2 порядка с постоянными коэффициентами
| Составим уравнение 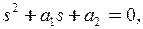 найдём
найдём 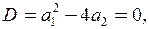 корни
корни 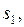 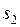 и пишем решение и пишем решение
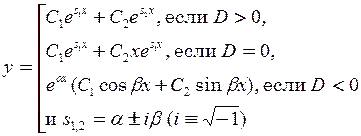
|
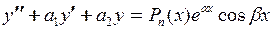 Линейное неоднородное ДУ 2 порядка с постоянными коэффициентами
Линейное неоднородное ДУ 2 порядка с постоянными коэффициентами
| Общее решение 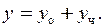 Здесь
Здесь 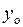 определяется из определяется из
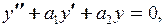 а
а 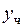 определяется подстановкой определяется подстановкой
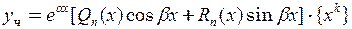 в исходное ДУ
в исходное ДУ
|
Дата: 2019-02-25, просмотров: 326.