МИНИСТЕРСТВО АГРАРНОЙ ПОЛИТИКИ УКРАИНЫ
КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Цикл инженерной механики
Теоретическая механика
Статика. Кинематика.
Конспект лекций. Ч I
для студентов направления 6.070104 «Морской
И речной транспорт», специальности
«Судовождение» ,
Направления 6.050702 «Электромеханика», специальности
«Электрические системы и комплексы транспортных средств»,
Направления 6.050503 «Машиностроение», специальности
«Оборудование перерабатывающих и пищевых производств»
Дневной и заочной форм обучения
Керчь, 2009г.
Автор: Максимов А.Б. к.т.н., доцент цикла «Инженерной механики». Керченского государственного морского технологического университета.
Рецензенты: Сушков О.Д. к.т.н, доцент, зав. кафедрой «ОПРП». КГМТУ
Мануилов В.В., технический директор ООО «Наладочно-монтажное предприятие».
Конспект лекций рассмотрен и одобрен на заседании цикла «Инженерной механики» КГМТУ
Протокол № 6 от 25.03.09г.
Конспект лекций утвержден на Методической комиссии МФ КГМТУ
Протокол № 7 от 15. 04.09г.
Методические указания утверждены на Методическом совете КГМТУ
Протокол № 5 от 22.04.09г.
© Керченский государственный морской технологический университет
| Содержание | |
| Введение | 4 |
| Статика | 5 |
| Лекция 1. Основные понятия и аксиомы статики | 5 |
| Лекция 2. Действия над силами. Система сходящихся сил | 11 |
| Лекция 3. Момент силы относительно центра (точки) | 17 |
| Лекция 4. Условия равновесия плоской системы сил | 23 |
| Лекция 5. Системы пар и сил в пространстве | 26 |
| Лекция 6. Трение. Центр тяжести твердого тела | 30 |
| Кинематика | 42 |
| Лекция 7. Кинематика точки | 42 |
| Лекция 8. Скорость и ускорение точки | 48 |
| Лекция 9. Поступательное движение твердого тела | |
| Вращательное движение твердого тела | 57 |
| Лекция 10. Плоскопараллельное движение твердого тела | 63 |
| Лекция 11. Определение ускорений точек тела при плоском | |
| движении | 72 |
| Лекция 12. Сложное движение точки | 82 |
| Приложения | 93 |
| 1. Программа по теоретической механике (извлечение) | 93 |
| 2. Вопросы, выносимые на модульный контроль | 97 |
| Использованная литература | 99 |
Введение
Конспект лекций состоит из двух разделов – «Статика» и «Кинематика».
Статика – это часть механики, в которой изучаются условия равновесия тела или группы тел, скрепленных между собой.
В разделе «Статика» рассмотрены основные виды связей и условия равновесия твердого тела под действием плоской и пространственной системы сил. Рассмотрены способы приведения произвольной системы сил как плоской, так и пространственной к единому центру определения центра тяжести тел.
Кинематика – часть механики, изучающая движения тел независимо от причин, побуждающих это движение. В кинематике не учитывается масса тела и силы, вызывающие движение.
В разделе «Кинематика» рассмотрены кинематика точки и твердого тела.
Основными вопросами кинематики точки являются: три способа задания движения точки; понятие о траектории движущейся точки; скорость и ускорение точки.
Рассмотрены способы определения скорости и ускорений точек твердого тела при плоско-параллельном движении.
Последняя лекция посвящена рассмотрению сложного движения точки.
Изучение курса теоретической механики основано на базе курсов высшей математики и физики. Знания, полученные при изучении теоретической механики, будут использованы при изучении курсов теории механизмов и машин и деталей машин, а также других специальных курсов.
В результате изучения курса теоретической механики студент должен:
– определять силы реакций опор твердого тела;
– определять скорость и ускорения твердого тела при различных видах движения;
– определять скорость и ускорения точки при сложном движении.
Условия задач взяты из «Сборника задач по теоретической механике» Мещерского В.И.
Статика
Лекция 1
Основные понятия и аксиомы статики
Статикой называется раздел механики, в котором излагается общее учение о силах и изучается равновесие материальных тел, находящихся под действием сил.
Рассматриваемые в статике материальные тела принимаются как абсолютно твердые тела.
Абсолютно твердым телом (а.т.т.) называется такое тело, расстояние между двумя точками которого всегда остается постоянным.
Таким образом, в статике считается, что деформация тел под действием сил отсутствует.
Чтобы твердое тело под действием некоторой системы сил находилось в равновесии (в покое), необходимо, чтобы эта система сил удовлетворяла определенным условиям равновесия.
В статике твердого тела решаются следующие основные задачи:
1. Сложение сил и приведение системы сил, действующих на твердое тело, к простейшему виду.
2. Определение условий равновесия действующих на твердое тело систем сил.
Основной характеристикой в статике является сила.
Сила – это величина, являющаяся количественной мерой механического взаимодействия материальных тел.
Сила является векторной величиной, поэтому ее действие характеризуется:
1. Численной величиной, или модулем силы;
2. Направлением действия;
3. Точкой приложения силы.
Связи и их реакции
Тело, перемещению которого в пространстве препятствует какие-нибудь другие тела, скрепленные или соприкасающиеся с данным, называется несвободным. Все то, что ограничивает перемещение данного тела в пространстве, называется связями.
Пример. Груз висит на веревке, ящик стоит на полу и т.д.
Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.
Силы, приложенные к телу, но не являющиеся реакциями, называются активными.
Направление силы реакции связи противоположно той, куда связь не дает перемещаться телу.
Сложение сил
Сложение двух сил
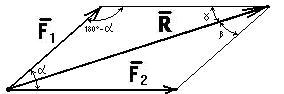
Пусть на тело действуют две силы, лежащие в одной плоскости (рис. 1.13).
.
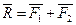
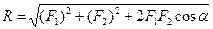Результирующая сила определяется по правилу параллелограмма, модуль силы определяется по теореме косинусов или синусов:
; 
.
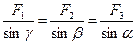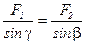Разложение сил
Вопросы для самоконтроля
1. Что изучает статика?
2. Что такое абсолютно твердое тело?
3. Основные виды связей и их реакции?
4. Геометрическое сложение сил?
Задачи, рекомендуемые для самостоятельного решения: 1.1 – 1.6 [2]
Литература: [1], [3], [4].
Лекция 2.
Решение задач статики
Для решения задач статики необходимо:
1. Выбрать тело, равновесие которого должно быть рассмотрено.
2. Освобождение тела от связей и изображение действующих на него заданных сил и реакций отброшенных связей.
3. Составление уравнений равновесия.
4. Определение искомых величин, проверка правильности решения и исследование полученных результатов.
Для решения задач на равновесие тела под действием сходящихся сил можно использовать следующие способы:
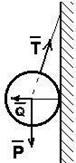а) Геометрический способ. Применяется если число сил, действующих на тело равно трем. При равновесии треугольник, построенный на этих силах, должен быть замкнутым.
б) Аналитический способ. Применяется при любом количестве сил, действующих на тело. В случае плоской системы сходящихся сил составляется два уравнения равновесия, а в случае пространственной системы сил – три.
 |
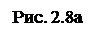Пример №3. К вертикальной гладкой стене АВ подвешен на тросе АС однородный шар. Трос составляет со стеной угол a, сила тяжести шара Р. Определить силу натяжения троса Т и давление шара на стену Q. Шар находится в равновесии под действием этих трех сил (рис. 2.8а).
Решение.
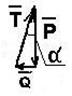Рассмотрим решение задачи геометрическим (графическим) способом. Так как шар находится в равновесии под действием трех сил, то эти силы сходящиеся. Точка, в которой сходятся эти силы, является геометрическим центром шара (точка О). Построим силовой треугольник (рис. 2.8б). Построение начинают с известной силы Р.
Силовой треугольник должен быть замкнут. В данном случае это прямоугольный треугольник. Тогда: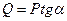 
; 
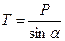
Ответ: ; .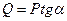
|
| |
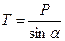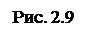
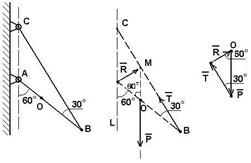
Определим силы, действующие на данную конструкцию:
Р – сила тяжести стержня АВ, так как стержень однородный, то сила приложена к его геометрическому центру (точка О).
Т – натяжение троса СВ, направлено вдоль СВ.
R – реакция в шарнире А (направление неизвестно) (рис. 2.9б).
Согласно принципу освобождаемости от связей, заменим связи соответствующими реакциями.
Так как система находится в равновесии под действием трех сил, то эти силы должны сходиться, а поэтому сила реакции R направлена от А к М (точка пересечения сил Р и Т).
Построим силовой треугольник. Для этого выберем произвольную точку О и отложим от нее известную силу Р, сохраняя ее направление. Из конца вектора Р под углом 300 проведем луч, который соответствует направлению силы Т (рис. 2.9в).
Так как <LAO = <AOM (как накрест лежащие углы), то угол <MOB = 1800 - 600 = 1200, тогда <OMB = 1800 – (1200 + 300) = 300, т.е. треугольник ОМВ равнобедренный: сторона ОМ = ОВ. Поэтому ОМ = ОВ = ОА, так как О является серединой АВ, а угол <АOM = 600, то треугольник АОМ является равносторонним. Поэтому <OАM = 600 = <AMO. Из точки О проводим луч под углом 600 к направлению силы Р до пересечения с направлением силы Т. Полученный треугольник прямоугольный, поэтому R = Psin300 = 20/2 = 10H.
Ответ: R = 10H.
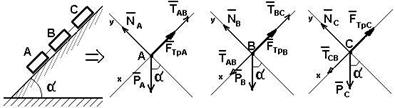
Пример №5. Три груза А, В и С массой 10, 20, и 60 кг соответственно лежат на плоскости, наклоненной под углом a к горизонту (рис. 2.10). Грузы соединены тросами, как показано на рисунке. Коэффициенты трения между грузами и плоскостью равны ¦А = 0,1, ¦В = 0,25, ¦С = 0,5 соответственно.
Определить угол a, при котором тела равномерно движутся вниз по плоскости. Найти также натяжение тросов ТАВ и ТВС.
Решение:
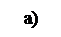Рассмотрим, какие силы действуют на каждое тело и запишем условие равновесия, так как тела движутся равномерно, то
сумма всех сил, действующих на тело равна нулю. На тело А действует сила тяжести РА, сила реакции опоры NА, сила трения FтрА и сила натяжения троса ТАВ (рис. 2.10б). Условие равновесия: РА + NА + FтрА + ТАВ = 0.
Выберем систему координат и спроектируем силы на оси:
Ось ОХ РАsina - РАcosa - ТАВ = 0.
Подставляя численные значения получим: 10sina - cosa - ТАВ = 0.
Рассмотрим, какие силы действуют на тело В: РВ - сила тяжести, FтрВ - сила трения, ТВА- сила натяжения троса со стороны груза А, ТВС - сила натяжения троса со стороны груза С, NВ - сила реакции опоры (рис. 2.10в). Тогда условие равновесия будет: РВ + NВ + FтрВ + ТВА + ТВС = 0.
Проектируя это уравнение на ось ОХ, получим:
РВsina - FтрВ + ТВА - ТВС = 0; учитывая, что ТВА = ТАВ:
РВsina - РВcosa*¦В + ТВА - ТВС = 0;
30sina - 30cosa*0.25 + ТВА - ТВС = 0;
На тело С действуют следующие силы: РС - сила тяжести, FтрС - сила трения, ТСВ- сила натяжения троса со стороны груза В, NС - сила реакции опоры (рис. 2.10г). Тогда условие равновесия при проектировании на ось ОХ будет:
РСsina - РСcosa*¦С – ТСВ = 0; так как ТВС = ТСВ,
60sina - 60*0,5cosa – ТВС = 0.
Получим систему из трех уравнений с тремя неизвестными:
Так как неизвестные силы перпендикулярны оси y, то на эту ось силы не проектируем.
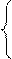10sina - cosa - ТАВ = 0 (1);
30sina - 7,5cosa + ТВА - ТВС = 0 (2);
60sina - 30cosa – ТВС = 0 (3).
Отсюда: ТАВ = 10sina - cosa; ТВС = 60sina - 30cosa.
Подставляя выражения ТАВ и ТВС в уравнение (2), получим:
100sina = 38.5cosa; tga = 0.385; a = arctg0.385; a = 210.
Из уравнения (1) получим: ТАВ = 10sin210 - cos210 = 10*0,358 – 0,93 = 2,67Н.
ТАВ = 2,67Н.
Подставляя численные данные в уравнение (3), получим:
ТВС = 60sin210 - 30cos210 = 60*0,358 – 30*0,93 = 6,42Н;
ТВС = 6,42Н.
Ответ: a = 210; ТАВ = 2,67Н; ТВС = 6,42Н.
Вопросы для самоконтроля
1. Аналитический способ сложения сил?
2. Что такое система сходящихся сил?
3. Теорема о трех силах?
Задачи, рекомендуемые для самостоятельного решения: 2.1 – 2.71 [2]
Литература: [1], [3], [4].
Лекция 3.
Эквивалентность пар
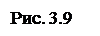Не изменяя оказываемого действия на твердое тело, можно пару сил, приложенную к телу заменить любой другой парой, лежащей в той же плоскости и имеющей тот же момент (рис. 3.9).
m(F) = m(P).
Следствия теоремы
1. Данную пару, не изменяя оказываемого ею на тело действия, можно переносить куда угодно в плоскости действия пары.
2. У данной пары, не изменяя оказываемого ею на тело действия, можно произвольно менять модули сил или длину плеча, сохраняя неизменным ее момент.
Вопросы для самоконтроля
1. Что такое момент силы относительно центра?
2. Что такое пара сил?
3. Приведение произвольной плоской системы сил к данному центру?
4. Сложение параллельных сил?
Задачи, рекомендуемые для самостоятельного решения: 3.1 – 3.14 [2].
Литература: [1], [3], [4].
Лекция 4.
Вопросы для самоконтроля
1. Три формы уравнений равновесия твердого тела?
2. Составление уравнений равновесия для составной конструкции?
Задачи, рекомендуемые для самостоятельного решения: 4.1 – 4.80 [2].
Литература: [1], [3], [4].
Лекция 5.
Вопросы для самоконтроля
1. Как определяется момент силы относительно оси?
2. Уравнения равновесия твердого тела под действием пространственной системы сил?
3. Приведение пространственной системы сил к заданному центру?
Задачи, рекомендуемые для самостоятельного решения: 6.1 – 6.21, 7.1 – 7.12, 8.1 – 8.44 [2].
Література: [1], [3], [4].
Лекция 6.
Законы трения скольжения
Причиной трения является, прежде всего, шероховатость поверхностей и наличие молекулярных сил сцепления прижатых друг к другу тел.
1. При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения, величина которой может принимать любые значения от 0 до значений Fпр, называемой предельной силой трения. Сила трения направлена в сторону, противоположную той, куда действующие силы стремятся сдвинуть тело.
2. Величина предельной силы равна произведению статического коэффициента трения на нормальное давление или нормальную реакцию:
Fпр = ¦0N.
3. Величина предельной силы трения не зависит от размеров соприкасающихся при трении поверхностей. При равновесии сила трения покоя: F £ ¦0N.
При движении сила трения направлена в сторону, противоположную движению, и равна произведению динамического коэффициента трения на нормальное давление: F = ¦N.
Значение динамического коэффициента ¦ зависит не только от материала и от состояния поверхности, но и от скорости движения.
Трение качения и верчения
Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.
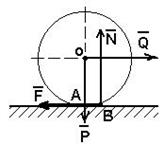
Рассмотрим круглый цилиндрический каток, лежащий на горизонтальной шероховатой поверхности (плоскости), вследствие деформации катка касания тел происходит вдоль некоторой площадки АВ (рис. 6.2).
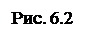Пусть Р – сила тяжести катка, радиусом R, к которому приложена сила Q. Под действием силы Q давление на поверхность возрастает от края А к краю В, поэтому сила реакции N смещена относительно центра катка О. Величина смещения (расстояние АВ) возрастает с увеличением силы Q до некоторой предельной величины К. Поэтому в предельном положении на каток будет действовать пара (Qпр, F) с моментом Qпр*R и уравновешивающая ее пара (N, P) с моментом Nк. Из равенства моментов определяем Qпр*R = Nk или Qпр = К*N/R.
При Q < Qпр каток находится в покое; при Q > Qпр – начинается качение.
Величина К называется коэффициентом трения; К измеряется в линейных единицах, например, в сантиметрах.
Понятие о трении верчения
Если к шару, лежащему на горизонтальной плоскости приложить пару сил с моментом М, расположенную тоже в горизонтальной плоскости, то пара будет стремиться повернуть шар вокруг вертикальной оси. Опыт показывает, что шар начнет вращаться только тогда, когда значение М будет больше некоторой предельной величины Мпр, определяемой равенством
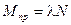, (6.1)
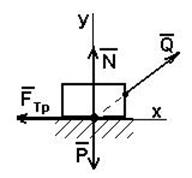где N – сила нормального давления на плоскость, равная в данном случае весу шара. Объясняется этот результат наличием трения верчения шара о плоскость. Входящий в равенство (6.1) коэффициент λ, имеющий размерность длины, называется коэффициентом трения верчения. По величине этот коэффициент меньше трения качения k.
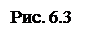
Пример. Определить, какую силу Q, направленную под углом a = 300 к горизонту, надо приложить к грузу массой 10кг, лежащему на горизонтальной поверхности, чтобы его сдвинуть с места, если статический коэффициент трения груза о плоскость ¦0 = 0,8 (рис. 6.3).
Решение : на данное тело действуют следующие силы:
P – сила тяжести = mg;
N – сила нормальной реакции опоры;
Fтр – сила трения;
Q – действующая сила.
При равновесии тела должно выполнятся условие: N + Q + P + Fтр = 0.
Выберем систему координат и спроектируем это векторное уравнение на оси Х и Y:
Q cosa - Fтр = 0; N + Q sina - P = 0;
Отсюда следует, что N = p – Q sina, так как Fтр = ¦0N, то
Q cosa = ¦0N = ¦0P – Q*¦0 sina или Q(cosa + ¦0 sina) = ¦0P, отсюда
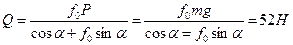
Ответ: Q = 52H.
Центр тяжести.
Центр параллельных сил
Рассмотрим систему параллельных и одинаково направленных сил F1, F2, …, Fn приложенных к телу в точках A1, A2, …, An. Эта система имеет равнодействующую R, направленную как слагаемые силы, а по модулю равна: R = å Fi.
Точка С, через которую проходит линия действия равнодействующей силы параллельных сил при любых поворотах этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол, называется центром параллельных сил.
Формулы для определения координат центра параллельных сил:
; 
; 
.
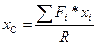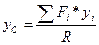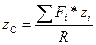Центр тяжести твердых тел
Твердое тело состоит из набора частиц, которые обладают силой тяжести. Силы тяжести всех этих частиц направлены к центру Земли, но, учитывая, что размеры Земли несоизмеримо больше размеров тела, то эти силы можно считать параллельными.
Таким образом, центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести частиц данного тела при любом положении тела в пространстве.
Координаты центра тяжести тела как центра параллельных сил определяются по формулам:
; 
; 
,
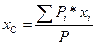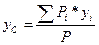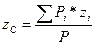где Pi – сила тяжести i-ой частицы тела;
P – сила тяжести всего тела: P = å Pi.
Координаты центра тяжести однородного тела:
; 
; 
,
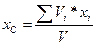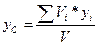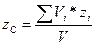где Vi – объем i-ой частицы тела;
V – объем тела, V = å Vi.
Координаты центра тяжести однородной линии:
; 
; 
,
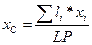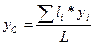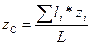где li – длина i-ой части линии;
L – длина всей линии, L = å li.
Примеры выполнения заданий
Задача 1 (способ разбиения)
Определить координаты центра тяжести плоской фигуры, представленной на
рис. 6.6:
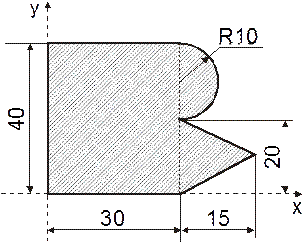
Рис. 6.6
Решение
Разбиваем данное плоское тело на части, для каждой из которых положение центра тяжести известно. Тогда координаты центра тяжести всего тела можно вычислить по формулам (1) и (2).
В данном случае тело разбиваем на прямоугольник ABCL, треугольник LFK и полукруг CDF (рис. 6.7):
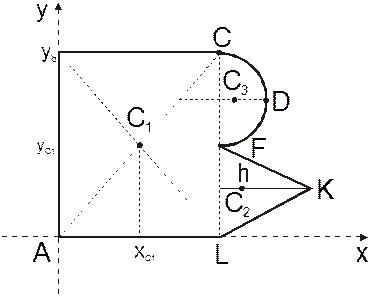
Рис. 6.7
Рассмотрим отдельно каждую часть фигуры:
Прямоугольник ABCL
Центр тяжести (С1) определяется на пересечении диагоналей АС и BL, т.е.
.
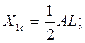
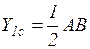Площадь определяется: S 1 = AL * AB
Подставляя численные значения, получим:
X1c = 15 мм; Y1c = 20 мм; S1 = 1200 мм 2 .
Треугольник LFK
Координаты центра тяжести (С2) определяются по формулам (3); (4).
Из рисунка видно, что координаты вершин являются:
L(30;0); F(30;20); K(45;10)
Площадь
,
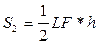где h – высота треугольника, опущенная из вершины К на сторону FL.
Подставляя численные значения, получим:
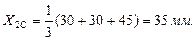
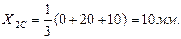
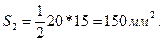
Полукруг CDF .
Координаты центра тяжести (С3) определяем по формуле (5).
Так как R = 10 мм; b = 20 мм;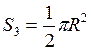 
, то, подставляя численные значения, получим:
X3C = 34 мм; Y3C = 30 мм; S3 = 157 мм2.
Для вычисления центра тяжести плоской фигуры составим таблицу:
| Номер элемента | Si мм2 | Xci, мм | Yci, мм | SiXci, мм3 | SiYci, мм3 |
| 1 | 1200 | 15 | 20 | 18000 | 24000 |
| 2 | 150 | 35 | 10 | 5250 | 1500 |
| 3 | 157 | 34 | 30 | 5350 | 4700 |
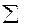
| 1507 | - | - | 28600 | 30200 |
В соответствии с формулами (1), (2) получим, что координаты центра тяжести всей фигуры будут:
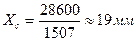
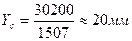
Ответ: координаты данной плоской фигуры: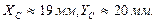 
Задача 2 (способ дополнения)
Определить площадь плоской фигуры, изображенной на рис. 6.8
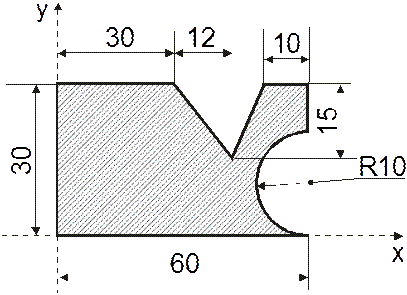
Рис. 6.8
Решение.
Разбиваем данное плоское тело на части согласно рисунку 6.9:
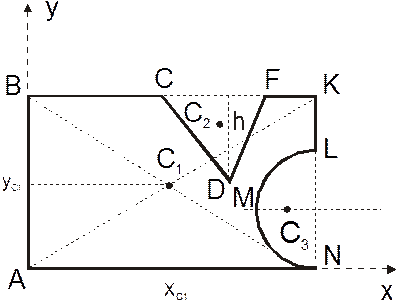
Рис. 6.9
| I часть II часть III часть | - - - | прямоугольник ABKN треугольник CDF полукруг LMN |
Причем площади дополняющих фигур треугольника CDF и полукруга LMN берутся с отрицательным знаком.
Рассмотрим отдельно каждую часть фигуры:
Прямоугольник ABKL
Центр тяжести (С1) определяется на пересечении диагоналей BN и AK,т.е.
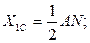
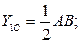
площадь определяется: S 1 = AN * BA
Подставляя численные значения, получим:
X1C = 30 мм.; Y1C = 15 мм.; S1 = 1800 мм2
Треугольник CDK
Координаты центра тяжести (С2) определяем по формулам (3), (4).
Из рисунка видно, что координаты вершин треугольника являются:
С(30;30); F(20;30); D(42;15)
Площадь
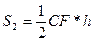
где h – высота треугольника, опущенная из вершины D на сторону CF.
Подставляя численные значения, получим:
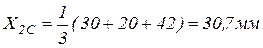
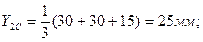
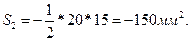
3. Полукруг MNL .
Координаты центра тяжести (С3) определяем по формуле (5).
Так как R = 10 мм; b = 20 мм;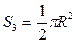 
, то, подставляя численные значения, получим:
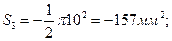
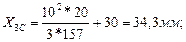
Y3C = 10 мм.
Для вычисления центра тяжести плоской фигуры составим таблицу:
| Номер элемента | Si Мм2 | Xci, мм | Yci, мм | SiXci, мм3 | SiYci, мм3 |
| 1 | 1800 | 30 | 15 | 54000 | 27000 |
| 2 | -150 | 30,7 | 25 | -4605 | -3750 |
| 3 | -157 | 34,3 | 10 | -5385,1 | -1570 |
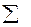
| 1493 | - | - | 44009,9 | 21680 |
В соответствии с формулами (1), (2) получим, что координаты центра тяжести всей фигуры будут:
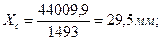
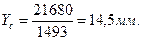
Ответ: координаты данной плоской фигуры: XC = 29,5 мм; YC = 14,5 мм.
Вопросы для самоконтроля
1. Что такое трение скольжения? Как определяется коэффициент трения скольжения?
2. Что такое трение качения и верчения? Как определяется коэффициенты трения качения и верчения?
3. Что такое центр тяжести тела?
4. Способы определения плоской фигуры?
Задачи, рекомендуемые для самостоятельного решения: 9.1 – 9.28 [2].
Литература: [1], [3], [4].
Кинематика
Лекция 7
Кинематика точки
Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.
Для определения положения движущегося тела (или точки) с тем телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, которая вместе с телом образует систему отсчета. Если координаты всех точек тела в выбранной системе отсчета остаются все время постоянными, то тело по отношению к этой системе отсчета находится в покое. Если координаты каких-нибудь точек тела с течением времени изменяются, то тело по отношению к данной системе координат находится в движении.
Движение тел совершается в пространстве с течением времени. В механике рассматривается трехмерное евклидовое пространство. Время является скалярной величиной, непрерывно изменяющейся величиной. Отсчет времени ведется от некоторого начального (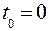 
), о выборе которого в каждом случае уславливаются. Разность между двумя последовательными моментами времени называется промежутком времени.
Кинематически задавать движение или закон движения тела (точки) – значит, задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.
Основная задача кинематики состоит в том, чтобы, зная закон движения данного тела (или точки), определить все кинематические величины, характеризующие тела в целом, так и движение каждой из его точек в отдельности (траектории, скорости, ускорения и т.п.).
Вначале изучим движения точки, а затем перейдем к изучению кинематики твердого тела.
Способы задания движения точки.
Траектория
Чтобы задать движение точки, надо задать ее в любом положении по отношению к выбранной системе отсчета в любой момент времени. Для задания движения точки можно применять один из следующих трех способов:
1. Естественный;
2. Координатный;
3. Векторный.
Естественный способ задания движения
Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория – прямая линия, то движение точки называется прямолинейным; а если кривая – то движение точки называется криволинейным.
Пусть кривая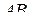 
является траекторией движения точки 
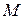относительно системы отсчета 
, 
, 
, 
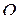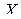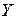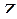, (рис. 1.1.).
Рис. 7.1.
Выберем на этой траектории какую-нибудь неподвижную точку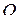 
, которую примем за начало отсчета; затем, рассматривая траекторию как криволинейную координатную ось, установим на ней положительное и отрицательное направление. Тогда положение точки 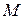будет однозначно определяться криволинейной координатой 
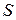, которая равна расстоянию от точки 
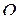до точки 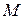. Чтобы знать положение точки 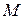на траектории, в любой момент времени надо знать зависимость:
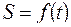(7.1.)
Уравнение (7.1.) выражает закон движения точки 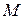вдоль траектории. Таким образом, чтобы задать движения точки естественным способом, надо знать:
1. Траекторию точки;
2. Начало отсчета на траектории;
3. Законы движения точки вдоль траектории в виде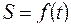 
.
Координатный способ задания движения
Положение точки по отношению к данной системе отсчета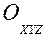 
, можно определить ее декартовыми координатами 
, 
, 
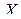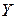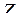(рис. 7.2.).
При движении все эти три координаты будут с течением времени изменяться. Чтобы знать закон движения точки, необходимо знать значения координаты точки для каждого момента времени, т.е. знать зависимости:
; 
; 
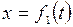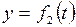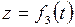. (7.2)
Уравнения (7.2) представляют собой уравнения движения точки в декартовых координатах.
В случае плоского движения, например, точка движется в плоскости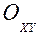 
, ее уравнения движения задаются в виде:
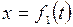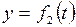, (7.3)
Рис. 7.2.
Уравнения (7.2), (7.3) представляют одновременно уравнения траектории точки в параметрической форме, где роль параметра играет величина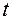 
. Исключив параметр 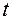, можно найти уравнение траектории в обычной форме, т.е. в виде, дающем зависимость между ее координатами:
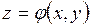– для пространственного движения;
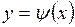– для плоского движения.
Векторный способ задания движения
Пусть точка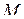 
движется по отношению к некоторой системе отсчета 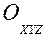. Положение этой точки можно определить, задав вектор 
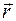, проведенный из начала координат 
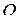в точку 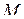. Вектор 
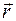называется радиусом – вектором точки 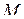. При движении точки 
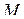вектор 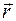будет с течением времени изменяться и по модулю и по направлению. Следовательно, 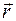можно задать вектором-функцией, зависящим от аргумента :
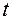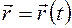(7.4.)
Геометрическое место концов вектора 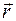, т.е. годограф этого вектора, определяет траекторию движущейся точки. Проектируя уравнение (7.4.) на оси координат получим:
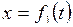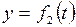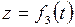; ; . (7.5).
Пример 1.
Заданы уравнения движения точки в координатной форме:
; 
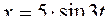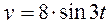(плоское движение). Значения 
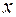и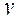 
в сантиметрах. Определить траекторию движения точки.
Решение.
Для определения траектории движения точки, необходимо исключить параметр 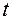из уравнений движения, заданных в координатной форме. Для этого возведем в квадрат данные уравнения:
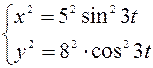, отсюда: 
.
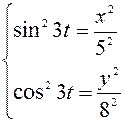Сложим соответственно левые и правые части полученных уравнений:
,
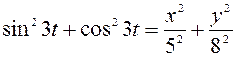Отсюда следует: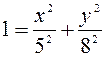 
, так как 
.
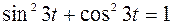Это есть каноническое уравнение эллипса с полуосями 5 и 8 см. Таким образом, данная точка совершает движение по эллипсу (рис.7.3.)
Рис. 7.3.
Ответ: траектория движения точки – эллипс.
Пример 2.
Уравнения движения точки на плоскости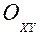 
задано:
, 
.
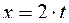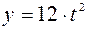Определить траекторию движения точки.
Решение.
Исключим параметр 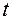из уравнений. Для этого из первого уравнения определим, что 
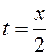и подставим во второе уравнение:
.
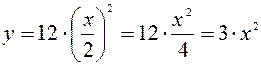Таким образом, получим: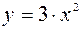 
.
Графиком траектории движения точки является парабола (рис. 7.4.).
Рис. 7.4
Ответ: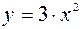 
– уравнение движения точки.
Пример 3.
Задано уравнение движения точки в векторной форме:
.
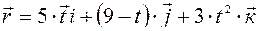Составить уравнение движения точки в координатной форме.
Решение.
Вследствие того, что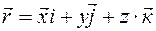 
, то отсюда следует:
; 
; 
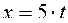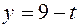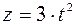
Ответ: уравнение движения точки: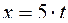 
; ; .
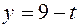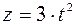Вопросы для самоконтроля
1. Что изучает кинематика?
2. Способы задания движения точки?
Задачи, рекомендуемые для самостоятельного решения: 10.1 – 10.23 [2].
Литература: [1], [3], [4].
Лекция 8
Вектор скорости точки
Скоростью называется векторная величина, модуль которой определяется изменением пройденного пути за единицу времени. Скорость будем обозначать символом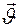 
, а ее модуль – 
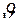, тогда:
; 
.
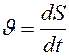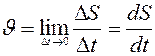Рис.8.1.
Так как скорость – вектор, то кроме модуля скорость имеет точку приложения и направление. Направление вектора скорости совпадает с направлением касательной к траектории движения точки в каждый момент времени.
Размерная скорость в СИ – м/с.
Вектор ускорения точки
Ускорением называется векторная величина, определяемая как изменение скорости в единицу времени.
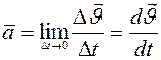(рис.8.2.)
Рис. 8.2
Размерность ускорения – м/с.
Определение скорости и ускорения точки при векторном способе задания движения (рис. 8.3)
Скорость точки определяется:
.
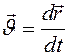Рис. 8.3
Ускорение точки определяется:
.
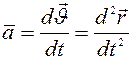Определение скорости точки
Так как вектор скорости точки определяется: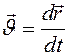 
, отсюда, учитывая уравнения, 
; 
; 
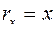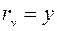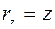, получим:
; 
; 
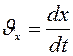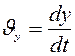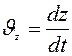или
; 
; 
.
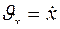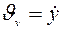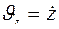Модуль скорости 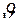определяется:
.
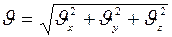Направление вектора скорости определяется через направляющие углы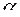 
, 
, 
:
; 
; 
.
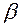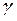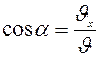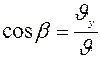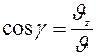Определение ускорения точки
Так как вектор ускорения точки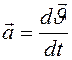 
, то, проектируя это уравнение на оси координат, получим:
; 
; 
;
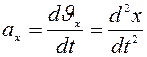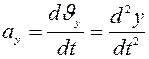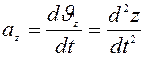или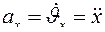 
; 
; 
.
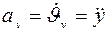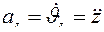Модуль и направление вектора ускорения определим соответственно по формулам:
;
; 
; 
,
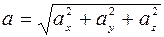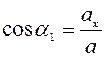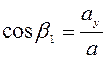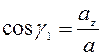где: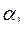 
, 
, 
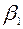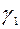– углы, образованные вектором ускорения с осями координат.
В случае плоского движения, например, в плоскости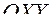 
проекции скорости и ускорения на ось 
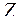равны нулю. При прямолинейном движении, например, вдоль оси 
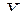уравнение движения задается в виде: 
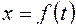, тогда:
; 
.
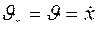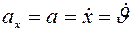Определение скорости при естественном способе задания движения
Пусть даны (рис. 8.4.) траектория точки и закон движения вдоль этой траектории в виде: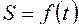 
.
За промежуток времени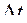 
точка проходит расстояние 
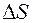, перемещаясь из положения 
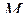в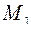 
, тогда скорость на этом участке можно определить:
.
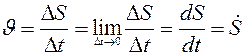Модуль скорости в данный момент времени определяется первой производной от расстояния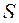 
точки по времени.
Направлен вектор скорости по касательной к траектории и приложен к точке траектории, соответствующей данному моменту времени.
Вопросы для самоконтроля
1. Определение скорости точки при различных способах задания движения?
2. Определение ускорения точки при различных способах задания движения?
Задачи, рекомендуемые для самостоятельного решения: 11.1 – 11.18, 12.1 – 12.39 [2].
Литература: [1], [3], [4].
Лекция 9
Вопросы для самоконтроля
1. Что такое поступательное движение твердого тела?
2. Какие характеристики определяют поступательное движение твердого тела?
3. Какие характеристики определяют вращательное движение твердого тела?
Задачи, рекомендуемые для самостоятельного решения: 13.1 – 13.20, 14.1 – 14.9. [2].
Литература: [1], [3], [4].
Лекция 10
Вопросы для самоконтроля
1. Что такое плоскопараллельное движение твердого тела?
2. Определение скорости тела при плоском движении?
3. Что такое мгновенный центр скоростей твердого тела?
4. Метод построения мгновенного центра скоростей?
Задачи, рекомендуемые для самостоятельного решения: 16.1 – 16.39 [2].
Литература: [1], [3], [4].
Лекция 11
Вопросы для самоконтроля
1. Определение ускорений точек твердого тела?
2. Определение углового ускорения твердого тела при плоском движении?
Задачи, рекомендуемые для самостоятельного решения: 18.1 – 18.36 [2].
Литература: [1], [3], [4].
Лекция 12
Сложное движение точки
Если точка движется одновременно по отношению к двум системам отсчета, из которых одна считается условно неподвижной, а другая движется по отношению к первой, то движение, совершаемое при этом точкой, называется составным или сложным.
Например, человек перемещается по вагону поезда (подвижная система отсчета), который движется по отношению к Земле (неподвижная система отсчета).
Рассмотрим сложное движение точки М, перемещающейся по отношению к подвижной системе отсчета ОXYZ, которая в свою очередь как-то движется относительно другой системы отсчета O1X1Y1Z1 условно названной неподвижной (рис. 12.1).
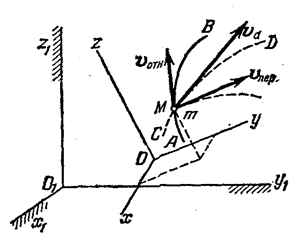
Рис. 12.1
Движение, совершаемое точкой М по отношению к подвижным осям координат, называется относительным движением. Траектория АВ описываемая в относительном движении называется относительной траекторией. Скорость движения точки М по отношению к осям OXYZ называется относительной скоростью (обозначается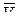 
), а ускорение точки в этом движении – относительным ускорением (обозначается 
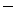). При вычислени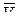и и 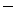оси OXYZ можно считать неподвижными.
Движение, совершаемое подвижной системой отсчета OXYZ и всеми неизменно связанными с ней точками пространства по отношению к неподвижной системе O1X1Y1Z1 является для точки М переносным движением.
Скорость неизменно связанной с подвижными осями OXYZ точки m, с которой в данный момент совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент времени (обозначается 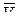), а ускорение этой точки – переносным ускорением точки М (обозначается ).
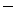На рис. 12.1 АВ – траектория точки М в относительном движении и 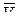к ней касательная в этой точке. Поскольку подвижная система координат OXYZ перемещается со скоростью 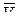, то результирующей скоростью будет 
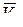, называемая абсолютной скоростью, которая является касательной к траектории CD, которая называется абсолютной траекторией. Движение точки М по абсолютной траектории – есть абсолютное движение, а ускорение – абсолютным ускорением.
Сложение скоростей
Теорема. При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей:
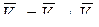, (12.1)
Рис. 12.2
На рис. 12.2: АВ – траектория точки М в относительном движении;
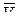– относительная скорость точки М;
А1В1– положение траектории точки М вследствие переносного движения.
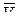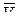Если угол между и составляет α, то формула (12.1) в скалярном виде будет:
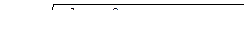, (12.2)
Сложение ускорений
Теорема Кориолиса. Абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного, характеризующего изменение относительной скорости в относительном движении; переносного, характеризующего изменение скорости в переносном движении и кориолисово, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости в относительном движении.
, (12.3)
где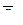 
– кориолисово ускорение.
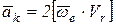. (12.4)
Кориолисово ускорение точки равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки. Если угол между векторам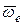и 
и 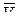составляет угол α, то модуль кориолисова ускорения будет равен:
. (12.5)
Частные случаи. Кориолисово ускорение будет равно нулю в следующих случаях:
1. Когда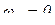 
, т.е. переносное движение является поступательным, или, если угловая скорость равна нулю;
2. Когда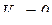 
, т.е. когда относительная скорость равна нулю;
3. Когда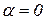 
и 
, т.е. когда относительное движение происходит по направлению, параллельному оси переносного вращения или, если в данный момент времени вектор 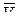параллелен этой оси.
Определение направления кориолисова ускорения (правило Жуковского Е.Н.):
Для определения направления кориолисова ускорения необходимо выполнить следующее:
5. провести плоскость, перпендикулярную вектору угловой скорости;
6. спроектировать на эту плоскость вектор скорости в относительном движении;
7. повернуть проекцию вектора скорости на 900 по ходу вращения переносного движения.
Пример 1.
Точка М в относительном движении из положения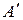 
движется по диагонали квадрата BCDA по закону 
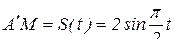, см. Квадрат BCDA вращается вокруг неподвижной оси по закону 
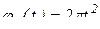, рад. Сторона квадрата CD = 4см. Определить абсолютную скорость и абсолютное ускорение при t = 1c.
Решение
Рис. 12.3
Определим абсолютную скорость точки М в момент времени t = 1c. Точка М перемещается по диагонали прямоугольника из положения 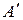. Так как относительное движение прямолинейное, то скорость точки М в относительном движении будет:
.
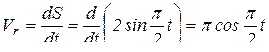При t = 1c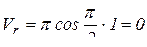 
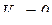(м/с); м/с.
Вращательное движение точки М вокруг оси ОО1 является переносным движением. Траектория переносного движения является окружность с радиусом r. Определим положение точки М на прямой АВ при t = 1c.
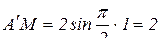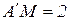(см); 
см.
Из треугольника MDK следует, что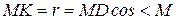 
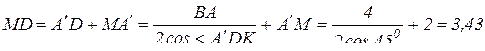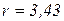(см);
см.
Так как точка М совершает в переносном движении вращение по окружности с радиусом r, то скорость в переносном движении будет:
,
где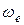 
– угловая скорость переносного движения.
;
.
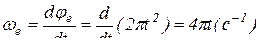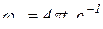Тогда
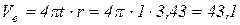(см/с);
см/с.
Вектор скорости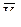 
направлен по касательной к траектории в точке М, т.е. перпендикулярно плоскости чертежа.
Так как при сложном движении точки:
,
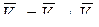то вследствие того, что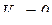
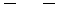, тогда 
см/с.
Абсолютная скорость точки М при t = 1c по модулю равна 43,1 см/с и направлена перпендикулярно плоскости чертежа (на нас).
Определим абсолютное ускорение точки М согласно теоремы сложения ускорений:
.
Так как в относительном движении точка движется по прямой, то:
.
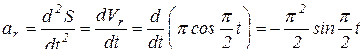При t = 1c,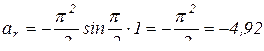 
(см/с2);
см/с2.
Вследствие движения точки М в переносном движении по окружности (рис. 12.4а):
,
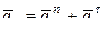где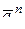 
– нормальная составляющая ускорения в переносном движении.
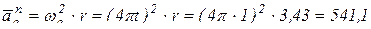(см/с2);
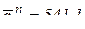см/с2., вектор нормальной составляющей ускорения направлен по радиусу к оси вращения.
;
– угловое ускорение в переносном движении;
; 
.
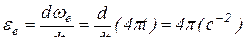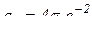Тогда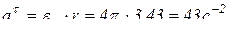 
; 
.
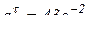Вектор касательной составляющей ускорения направлен в сторону направления вектора скорости (так как движение ускоренное, вследствие того, что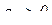 
), т.е. перпендикулярно плоскости чертежа (на нас).
а) б)
Рис. 12.4
Определим кориолисово ускорение:
или в скалярной форме:
,
где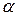 
– угол между векторам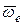и и .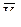
Так как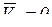 
, то и кориолисово ускорение равно нулю, т.е.:
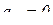см/с2.
В результате проведенных вычислений установлено, что на точку М в момент времени t = 1c действует три составляющих ускорения: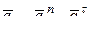 
(рис. 12.4б). Векторы 
лежат в плоскости чертежа и угол между ними составляет 450, тогда модуль суммы этих двух векторов будет:
,
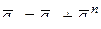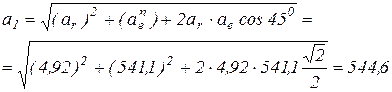(см/с2);
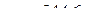см/с2.
Вектор 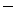находится в плоскости чертежа, а вектор 
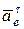– перпендикулярен плоскости чертежа, тогда результирующий вектор – вектор абсолютного ускорения будет:
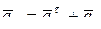
или в скалярной форме:
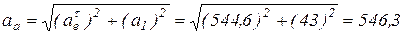(см/с2);
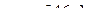см/с2.
Ответ: см/с, 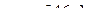см/с2.
Пример 2.
Точка М перемещается по окружности диска радиусом R = 2 см по закону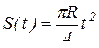 
из положения А. Диск вращается вокруг неподвижной оси по закону 
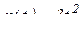. Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1c.
Решение
Рис. 12.5
R = 2см;
l = 5см.
Анализ характера движения точки М (рис. 12.5) свидетельствует, что движение по окружности диска радиусом R является относительным, а движение диска вокруг неподвижной оси – переносное движение.
Определим положение точки М на окружности диска в момент t = 1c:
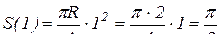(см).
Длина дуги, пройденная точкой М за 1с, составляет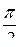 
см. Определим длину дуги в радианах:
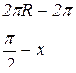
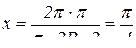(рад.)
Отсюда следует, что дуга, пройденная точкой М за 1с, составляет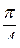 
рад., или 900 (положение М). Направление вектора скорости 
будет направлено по касательной к окружности в этой точке (рис. 12.5).
Определим абсолютную скорость точки М в момент t = 1c. По правилу сложения скоростей:
.
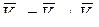Модуль скорости в относительном движении будет:
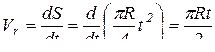; при t = 1c.
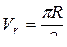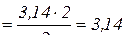(см/с) 
см/с.
В переносном движении точка М совершает вращательное движение по окружности с радиусом 
вокруг неподвижной оси (рис. 12.6а).
а) б) в)
Рис. 12.6
Направление вектора переносной скорости 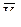перпендикулярно плоскости чертежа в сторону «от нас».
Модуль скорости 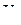определим:
,
где 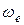– угловая скорость вращения диска вокруг оси.
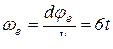; при t = 1c 
.
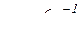Тогда
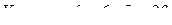(см/с);
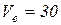см/с.
Векторы скоросте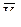й и 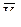ортогональны, так как расположены в двух взаимно пересекающихся плоскостях. Поэтому модуль результирующего вектора 
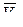определим:
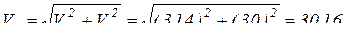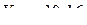(см/с);
см/с.
Определим абсолютное ускорение точки М в момент времени t = 1c. Согласно правилу сложения ускорений:
.
В относительном движении ускорение точки М разложим на две составляющие 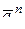и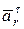 
, так точка движется по окружности (рис. 12.6б):
,
где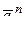 
– нормальная составляющая вектора ускорения точки М в относительном движении.
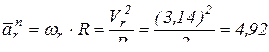(см/с); 
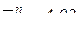см/с.
Вектор 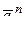направлен по радиусу к центру окружности О.
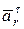– касательная составляющая вектора ускорения точки М в переносном движении.
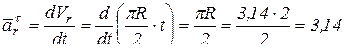(см/с2); 
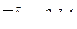см/с2.
Вектор 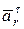направлен по касательной и окружности и совпадает с направлением вектора скорости, так как движение ускоренное.
Так как в переносном движении точка М движется по окружности вокруг неподвижной оси, то ускорение разложим на составляющие (рис. 12.6а):
,
где 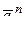– нормальная составляющая вектора ускорения в переносном движении.
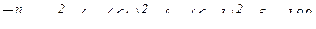(см/с2); 
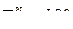см/с2.
Вектор 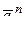направлен к неподвижной оси.
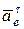– касательная составляющая вектора ускорения в переносном движении.
;
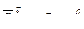– угловое ускорение диска в переносном движении:
; 
.
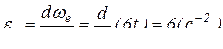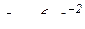(см/с2);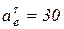 
см/с2.
Вектор 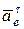направлен перпендикулярно плоскости чертежа и совпадает с направлением вектора скорости переносного движения (так как движение ускоренное).
Определим кориолисово ускорение:
.
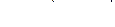Модуль кориолисова ускорения равен:
,
где 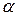– угол между векторам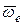и и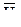 
.
Согласно «правила буравчика» в данном случае вектор угловой скорости переносного движения направлен параллельно неподвижной оси, вокруг которой вращается диск. Тогда расположение векторов 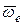и 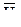будет таким, как представлено на рис. 12.6в. В этом случае вектор кориолисова ускорения, согласно правила Жуковского, будет направлен перпендикулярно плоскости чертежа «на нас».
Модуль 
будет равен:
(см/с2);
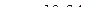см/с2.
Таким образом, на точку М действуют пять составляющих ускорений (рис. 12.7).
Рис. 12.7
Векторы 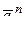и 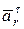лежат вдоль одной прямой в одну сторону, поэтому сумма этих векторов будет:
,
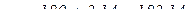(см/с2).
Векторы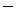 
и 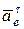направлены вдоль одной прямой, но в противоположные стороны, тогда результирующий вектор 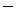будет:
,
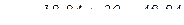(см/с2).
Получившаяся система векторов 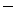, 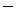и 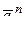образуют ортогональную систему, т.е. взаимноперпендикулярны, поэтому результирующий вектор 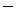можно представить:
,
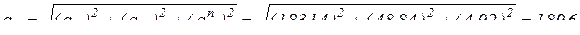(см/с2)
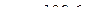см/с2.
Ответ: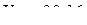 
см/с, 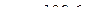см/с2.
Вопросы для самоконтроля
1. Что такое сложное движение точки?
2. Что такое относительное движение? Его кинематические характеристики?
3. Что такое переносное движение? Его кинематические характеристики?
4. Что такое абсолютное движение? Его кинематические характеристики?
5. Как определяется абсолютная скорость точки?
6. Теорема Кориолиса?
7. Как определяется величина и направление кориолисова ускорения?
Задачи, рекомендуемые для самостоятельного решения: 22.1 – 22.24, 23.1 – 23.66 [2].
Литература: [1], [3], [4].
Приложения
Приложение 1
Статика твердого тела
Основные понятия и аксиомы статики
Предмет статики. Основные понятия статики: материальная точка, система материальных точек, абсолютно твердое тело, сила, система сил, эквивалентные системы сил, равнодействующая, уравновешенная система сил, силы внешние и внутренние. Аксиомы статики. Связи и реакции связей. Основные виды связей и их реакции: гладкая плоскость, поверхность и опора, идеальный стержень, идеальная нить, цилиндрический и сферический шарниры (подпятник), жесткое защемление.
Система сходящихся сил
Геометрический и аналитический способы сложения сил. Сходящиеся силы. Равнодействующая сходящихся сил. Геометрические и аналитические условия равновесия пространственной и плоской систем сходящихся сил. Теорема о равновесии трех непараллельных сил.
Теория пар сил
Момент силы относительно точки (центра) как вектор. Пара сил. Момент пары сил как вектор. Теорема об эквивалентности пар. Сложение пар, произвольно расположенных в пространстве. Условия равновесия системы пар.
Приведение произвольной системы сил к данному центру
Теорема о параллельном переносе силы. Основная теорема статики о приведении системы сил к данному центру. Главный вектор и главный момент системы сил.
Система сил, произвольно расположенных на плоскости
(плоская система сил)
Алгебраическая величина момента силы. Вычисление главного вектора и главного момента плоской системы сил. Частные случаи приведения плоской системы сил: приведение к паре сил, к равнодействующей и случай равновесия. Аналитические условия равновесия плоской системы сил. Три вида условий равновесия системы сил на плоскости. Условия равновесия плоской системы параллельных сил. Теорема Вариньона о моменте равнодействующей относительно точки.
Сосредоточенные силы и распределенные нагрузки
Силы, равномерно распределенные по отрезку прямой, их равнодействующая. Реакция жесткого защемления. Равновесие системы тел. Статически определимые и статически неопределимые системы. Равновесие при наличии сил трения. Коэффициент трения. Предельная сила трения. Угол и конус трения.
Система сил, произвольно расположенных в пространстве
(пространственная система сил)
Момент силы относительно оси и его вычисление. Зависимость между моментами силы относительно оси, проходящей через этот центр. Формулы для вычисления моментов сил относительно трех координатных осей. Вычисление главного вектора и главного момента пространственной системы сил. Частные случаи приведения пространственной системы сил: приведение к паре сил, к равнодействующей, к динамическому винту и случай равновесия. Аналитические условия равновесия произвольной пространственной системы сил. Теорема Вариньона о моменте равнодействующей относительно оси.
Центр параллельных сил и центр тяжести
Центр параллельных сил. Формулы для определения координат центра параллельных сил. Центр тяжести твердого тела, формулы для определения его координат. Координаты центров тяжести однородных тел (центры тяжести объема, площади, линии). Способы определения положения центров тяжести тел. Центры тяжести дуги окружности, треугольника, кругового сектора.
Кинематика
Введение в кинематику
Предмет кинематики. Пространство и время в классической механике. Относительность механического движения. Система отсчета. Задачи кинематики.
Кинематика материальной точки
Векторный способ задания движения материальной точки. Траектория движения точки. Скорость движения точки, как производная по времени ее радиус-вектора. Ускорение движения точки, как производная по времени ее вектора скорости.
Координатный способ задания движения материальной точки (в прямоугольных декартовых координатах). Определение траектории движения точки. Определение скорости и ускорения точки по их проекциям на координатные оси.
Естественный способ задания движения материальной точки. Естественный трехгранник. Алгебраическая величина скорости точки. Определения ускорения точки по его проекциям на оси естественного трехгранника, касательное и нормальное ускорение точки. Равномерное и равнопеременное криволинейное движение материальной точки, законы этих движений.
Кинематика твердого тела
Поступательное движение
Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном его движении.
Вращение твердого тела вокруг неподвижной оси
(вращательное движение)
Уравнение или закон вращательного движения твердого тела. Угловая скорость и угловое ускорение твердого тела. Законы равномерного и равнопеременного вращения. Скорость и ускорение отдельной точки твердого тела, вращающегося вокруг неподвижной оси. Векторы угловой скорости и углового ускорения вращающегося твердого тела. Выражение скорости точки вращающегося тела и ее касательного и нормального ускорений в виде векторных произведений. Передача вращательного движения. Передаточное отношение и передаточное число.
Плоскопараллельное (плоское) движение твердого тела
Плоское движение твердого тела и движение плоской фигуры в ее плоскости. Уравнение движения плоской фигуры. Разложение движения плоской фигуры на поступательное вместе с полюсом и вращательное вокруг полюса. Независимость угловой скорости и углового ускорения фигуры от выбора полюса. Определение скорости любой точки плоской фигуры как геометрической суммы скорости полюса и скорости этой точки при вращении фигуры вокруг полюса. Теорема о проекциях скоростей двух точек фигуры (тела) на прямую их соединяющую. Мгновенный центр скоростей. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. Определение ускорения любой точки плоской фигуры как геометрической суммы ускорения полюса и ускорения этой точки при вращении фигуры вокруг полюса. Понятие о мгновенном центре ускорений.
Движение твердого тела вокруг неподвижной точки
(или сферическое движение)
Углы Эйлера. Уравнение движения твердого тела вокруг неподвижной точки. Мгновенная ось вращения тела. Векторы угловой скорости и углового ускорения тела. Определение скоростей и ускорений точек твердого тела, имеющего одну неподвижную точку.
Общий случай движения свободного твердого тела
Разложение движения свободного твердого тела на поступательное и вращательное. Уравнение движения свободного твердого тела. Определение скоростей и ускорений точек свободного твердого тела в общем случае.
Сложное движение материальной точки и твердого тела
(составное движение)
Абсолютное и относительное движение точки, переносное движение точки. Относительная, переносная и абсолютная скорость и относительное, переносное и абсолютное ускорение материальной точки. Теорема о сложении скоростей. Теорема Кориолиса о сложении ускорений. Модуль и направление ускорения Кориолиса. Случай поступательного переносного движения.
Сложное движение твердого тела. Сложение поступательных движений. Сложение мгновенных вращений твердого тела вокруг пересекающихся и параллельных осей. Пары мгновенных вращений. Кинематический винт. Мгновенная винтовая ось.
Приложение 2
Вопросы, выносимые на модульный контроль.
1. Аксиомы статики. Основные типы балок и их реакции.
2. Система сходящихся сил. Условия равновесия системы сходящихся сил.
3. Момент силы относительно точки и оси. Их взаимозависимость.
4. Пара сил. Теоремы об эквивалентности и сложении пар сил.
5. Приведение силы и системы сил к заданному центру.
6. Вычисление главного вектора и главного момента пространственной системы сил.
7. Случаи приведения пространственной системы сил. Условия равновесия пространственной системы сил.
8. Приведение пространственной системы сил к равнодействующей.
9. Теоремы Вариньона для плоской и пространственной системы сил.
10. Приведение пространственной системы сил к двум скрещивающимся силам или силовому винту (динаме).
11. Случаи приведения плоской системы сил к заданному центру. Условия равновесия плоской системы сил.
12. Сосредоточенные силы и распределенные нагрузки. Реакция жесткой заделки.
13. Центр тяжести твердого тела, плоской фигуры, материальной линии.
14. Равновесие при наличии сил трения.
15. Основные понятия кинематики. Способы задания движения точки.
16. Определение вектора скорости и ускорения при векторном способе задания движения точки.
17. Определение вектора скорости и ускорения при координатном способе задания движения точки.
18. Определение вектора скорости и ускорения при координатном способе задания движения точки.
19. Теорема о траекториях, скоростях и ускорениях точек поступательно движущегося тела.
20. Вращательное движение твердого тела.
21. Линейные характеристики точек вращающегося твердого тела и их векторное представление.
22. Угловые характеристики точек вращающегося твердого тела и их векторное представление.
23. Разложение плоского движения твердого тела.
24. Теорема о скоростях точек плоской фигуры и ее следствия.
25. Мгновенный центр скоростей. Определение с помощью МЦС скорости любой точки плоской фигуры.
26. Теорема об ускорениях точек плоской фигуры и ее следствия.
27. Мгновенный центр ускорений. Определение с помощью МЦУ ускорения любой точки плоской фигуры.
28. Сложное движение точки. Разложение сложного движения на переносное и относительное.
29. Теорема о сложении скоростей при сложном движении.
30. Теорема Кориолиса.
31. Модуль и направление кориолисова ускорения.
Список литературы
1. Тарг С.М. Краткий курс теоретической механики. Учебник. – М.: Наука. 1974 – 478с.
2. Мещерский И.В. Сборник задач по теоретической механике. Учебное пособие. – М.: Наука. 1986. – 448с.
3. Костюченко В.А., Булгаков А.М., Березовый Н.Г. Теоретическая механика. Кинематика. Учебное пособие. Методические указания и задания для выполнения расчетно-графических работ. – Киев. НАУ. 2001. – 126с.
4. Максимов А.Б. Теоретическая механика. Кинематика. Методические указания к выполнению практических занятий. Керчь. КГМТУ. 2009. – 122с.
© Александр Борисович Максимов
Теоретическая механика. Конспект лекций. Статика. Кинематика. Ч I.
Тираж 100 экз. Подписано к печати _________
Заказ № _________ Объем 2,6 п.л.
Издательство «Керченский государственный морской технологический университет». 98309, г.Керчь, Орджоникидзе, 82.
МИНИСТЕРСТВО АГРАРНОЙ ПОЛИТИКИ УКРАИНЫ
КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Цикл инженерной механики
Теоретическая механика
Статика. Кинематика.
Конспект лекций. Ч I
для студентов направления 6.070104 «Морской
и речной транспорт», специальности
«Судовождение» ,
Дата: 2019-02-25, просмотров: 207.
