Отказы, возникающие в процессе испытаний или эксплуатации, могут быть вызваны неблагоприятным сочетанием различных факторов — рассеянием действующих нагрузок, отклонением от номинального значения механических характеристик материалов, неблагоприятным сочетанием допусков в местах сопряжения и т. п. Поэтому в расчетах надежности технических систем различные параметры рассматривают как случайные величины, которые могут принимать то или иное значение, неизвестное заранее.
Различают случайные величины прерывного (дискретного) и непрерывного типов. Условимся случайные величины в дальнейшем обозначать большими буквами, а их возможные значения — соответствующими малыми. Для каждого числа х в диапазоне изменения случайной величины Х существует определенная вероятность Р(Х<х) того, что Х не превышает значения х. Вероятность этого события называют функцией распределения:
F(х) = Р (Х<х). (8.1)
Функция распределения — универсальная характеристика, так как она является функцией как непрерывных, так и дискретных случайных величин. Функция (х) относится к неубывающим функциям — х монотонно возрастает при непрерывных процессах и ступенчато возрастает при дискретных процессах. В пределах изменения случайной величины Х эта функция изменяется от 0 до 1:
F (-∞) = 0; F(∞) = 1
Производную от функции распределения по текущей переменной называют плотностью распределения f x = dF (x) / d x, (8.2)
которая характеризует частоту повторений данного значения случайной величины. В теории надежности величину f(x) называют плотностью вероятности. Плотность распределения есть неотрицательная функция своего аргумента ƒ(x) ≥ 0.
Интеграл в бесконечных пределах от плотности распределения равен единице:
∞
∫ f (x)dx = 1.
− ∞
В ряде случаев в качестве характеристик распределения случайных величин достаточно использовать некоторые числовые величины, среди которых в теории надежности наиболее употребительными являются математическое ожидание (среднее значение), мода и медиана (характеризуют положение центров группирования случайных величин на числовой оси), дисперсия, среднее квадратическое отклонение и коэффициент вариации (характеризуют рассеяние случайной величины). Значения n, g характеристик, полученные по результатам испытаний или эксплуатации, называют статистическими оценками. Характеристики распределения используют для прогнозирования надежности.
Для дискретных случайных величин математическое ожидание Mx равно сумме произведений всех возможных значений Х на вероятности этих значений:
Mx = 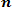
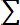


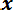
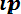
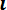


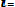
 . (8.3)
. (8.3)
Математическое ожидание для непрерывной случайной величины выражается интегралом в бесконечных пределах от произведения непрерывно изменяющихся возможных значений случайной величины на плотность распределения
Mx = 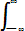
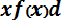
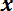 . (8.4)
. (8.4)
Математическое ожидание случайной величины непосредственно связано с ее средним значением. При неограниченном увеличении числа опытов среднее арифметическое значение величины х приближается к математическому ожиданию и называется оценкой среднего значения:
-
х = (1 / n 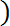



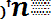
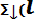
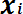

 ,
,
(8.5) где n - общее число опытов; xi - текущее значение случайной величины.
Дисперсией (D) случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания. Для дискретной случайной величины дисперсия равна:
Dx= 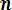
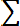

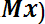
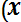
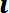



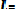
 2 (8.6)
2 (8.6)
Для непрерывной случайной величины дисперсия определяется из выражения
2
Dx = 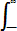
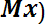
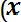

 f (x)dx. (8.7)
f (x)dx. (8.7)
Оценка дисперсии случайной величины:
- 2
Dx* = (1/n-1) 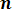
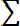

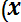
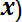
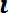


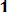
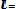
 (8.8)
(8.8)
Дисперсия случайной величины является характеристикой рассеяния — разбросанности значений случайной величины около ее математического ожидания. Размерность дисперсии соответствует квадрату размерности случайной величины. Для наглядности в качестве характеристики рассеяния удобнее использовать величину, размерность которой совпадает с размерностью случайной величины. Такой характеристикой может быть среднее квадратическое отклонение σx, которое определяется как корень квадратный из дисперсии:
σ х = √ Dx . (8.9)
Для оценки рассеяния с помощью безразмерной величины используют коэффициент вариации, который равен:
ʋх = σх / Мх. (8.10)
Модой случайной величины называют ее наиболее вероятное значение или то ее значение, при котором плотность вероятности максимальна.
Медиана характеризует расположение центра группирования случайной величины.
Площадь под графиком функции плотности распределения делится медианой пополам.
Квантиль — значение случайной величины, соответствующее заданной вероятности.
Квантиль, соответствующую вероятности 0,5, называют медианой.
Аналогично предыдущим характеристикам понятия моды и медианы даны в статистической трактовке. Для симметричного модального (т.е. имеющего один максимум) распределения математическое ожидание, мода и медиана совпадают.
Пример 8.1. Функция распределения непрерывной случайной величины
Х задана выражением
при 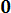
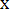


F x =ax3 при 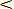

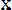
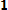
 при
при
Найти коэффициент а и плотность распределения f(x).
Р е ш е н и е. Так как функция распределения случайной величины Х непрерывна, то при х= 1, а.х3 = 1, откуда а = 1.
Плотность распределения выражается соотношением
при 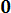
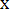


f(x)=dF/dx 3ax2 при 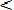

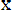
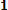
 при
при
Пример 8.2. Плотность распределения случайной величины Х описывается выражением
0 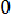
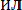
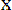
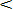
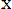


 при х ax при 0
при х ax при 0
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины.
Р е ш е н и е. Математическое ожидание найдем по формуле (7.4):
1 1
M = ∫ xf x dx = ∫ xaxdx = a /3
0 0
Для определения дисперсии используем формулу (5.7):
1
Dx = ∫ (x – a2/3)axdx = a(1/4 – 2a/9 +a2/18).
0
Среднее квадратическое отклонение соответственно равно:
σ x = √ Dx √ a(1/4 – 2a/9 +a2/18).
Пример 8.3. При проведении одного опыта может появиться или не появиться некоторое событие А. Вероятность появления события А равна р, а вероятность непоявления этого события - 1- p = q.
Определить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х — число появлений события А.
Р е ш е н и е. Ряд распределения случайной величины Х можно записать в виде таблицы:
xi 0 1 pi q p
По формуле (7.3) находим математическое ожидание:
Mx = 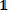



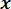
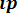

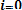
 = 0q + 1p = p.
= 0q + 1p = p.
Дисперсию величины Х определим по формуле (5.6).
Dx = ∑ (xi – Mx)2 pi = pq
Среднее квадратическое отклонение равно:
σ = 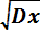
=
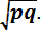
Пример 8.4. При эксплуатации сложной технической системы получены статистические данные, которые сведены в таблицу. Определить коэффициент готовности системы.
Таблица
Статистические данные, полученные при эксплуатации сложной технической системы
Номер Число отказов Время, ч
системы, mi восстановление Работы, tр Суммарное
п.п отказа, tв,i восстановление
m i tв,i
| 1 2 2 5 3 6 4 4 5 8 6 10 7 15 8 20 | 1 2 4 3 2 5 2 3 | 200 300 400 300 600 700 900 1000 | 2 10 24 12 16 50 30 60 |
| Всего 70 Наработка на отказ | - | 4400 | 204 |
| 8 8 | |||
Tо = Σtр/Σmi = 4400/70 = 62,8 ч.
i=1 i=1
Среднее время восстановления
8 8
Tв = Σmi tв.i/Σmi = 204/70 = 2,9 ч.
i=1 i=1
По формуле (8.3) по вычисленным значениям Tо и Tв находим коэффициент готовности системы:
Кr= 62,8/(62,8+2,9) = 0,95
Лекция 9
Дата: 2019-02-25, просмотров: 532.