Следует отметить, что в практике проектирования технических систем часто используют структурные схемы надежности с параллельнопоследовательным соединением элементов. Так, например, часто при проектировании систем с радиоэлектронными элементами применяют схемы, работающие по принципу два из трех, когда работоспособность обеспечивается благодаря исправному состоянию любых двух элементов. Надежность такой схемы соединения определяют по формуле
p(t) = p3(t) +3p2(t)q(t). (10.6)
где p(t) — надежность каждого элемента за время работы t одинакова; q(t)=1- p(t).
Широкое применение в проектировании нашли так называемые мостиковые схемы.
Надежность такой схемы определяют из соотношения вида
Р(t) = p5(t) + 5p4(t) q(t) + 8p3(t) q2(t) + 2p2(t) q3(t). (10.7)
Здесь все элементы также имеют одинаковую надежность.
Различают структурные схемы надежности с поканальным и поэлементным резервированием.
Структурная схема надежности с поканальным резервированием показана на рис. 10.3.
| Р |
| 1 |
| n |
| P2n |
………P21 Р22 .……………………………………………………………………………….
Pk1 Pk2 …….
| pkn |
Рис. 10.3. Структурнaя схема надежности с поканальным резервированием
Формула надежности выглядит так:
P = [1-(1- p11 p12…pin )(1-p21p22…p2n)(1-pk1pk2…pnk)] (10.8) При рi j = рj
P = 1-(1- p1p2…pn)k (10.9)
Если pij = р, то
P = l- (l - pn)k (10.10)
В практике проектирования часто используют структурную схему надежности с поэлементным резервированием (рис. 10.4).
| ……… ….. |
| Р |
| 11 |
| Р |
| 21 |
| Р |
| 12 |
| P1k |
| Р |
| 22 |
| P2k |
| Р |
| 1 |
| n |
| Р |
| 2 |
| n |
| pkn |
Рис.10.4. Структурная схема надежности с поэлементным резервированием
Надежность такой системы определяют по формуле:
P = [l - (1- pl1)(l - p21)...(l – p1k)][l - (l - p12)(1- p22)...(l – p2k)] …
...[1- (1- p1n)(1- p2n)...(1- pkn)]. (10.11)
При pij = pj
P = [l - (l - p1)k][1- (l - p2)k]…[1- (l - pn)k]. 10.12)
Если рij = p, то
P = [l - (l - p)k]n . (10.13)
Структурная схема с поэлементным резервированием имеет более высокую надежность по сравнению с поканальным резервированием.
Пример 10.2. Техническая система предназначена для выполнения некоторой задачи. Сцелью обеспечения работоспособности система
| спроектирована со смешанным соединением элементов |
| ( |
| рис |
| . 10.5.). |
| Рис |
| 9.5 |
| . |
| . |
| соединением |
| смешанным |
| со |
| надежности |
| схема |
| Структурная |
| Р |
| 1 |
| Р |
| 2 |
| Р |
| 3 |
| Р |
| 5 |
| Р |
| 7 |
| Р |
| 8 |
| Р |
| 9 |
| Р |
| 4 |
| Р |
| 6 |
элементов
Определить надежность системы, если известно, что надежность ее элементов равна:
p1=0,99; p2=0,98; p3=0,9; p4=0,95; p5=0,9; p6=0,9; p7=0,8; p8=0,75; p9=0,7.
Решение. При расчете надежности воспользуемся формулами как для последовательного, так и для параллельного соединения элементов: Р = p1 p2[1- (1- p3 p4)(1- p5 p6)][1- (1- p7)(1- p8)(1- p9)] =
= 0,99.0,98[1- (1- 0,9.0,95)(1- 0,9.0,9)][1- (1- 0,8)(1- 0,75)(1- 0,7)] = 0,927.
Cтруктурная схема, в которой элементы, отказ которых приводит к отказу всей системы, изображаются последовательно, а резервные элементы или цепи – параллельно.
Разницу между конструктивной (монтажной) схемой и структурной схемой надёжности системы можно показать на примере работы двух фильтров гидросистемы, которые для повышения надежности работы могут быть установлены последовательно или параллельно (рис.10.6).
Конструктивная Структурная схема
| схема |
| Засорение сетки |
| Разрыв сетки |
Рис.10.6. Конструктивные и структурные схемы надежности соединения фильтров при различных видах отказов
Отказ фильтра может произойти в результате двух основных причин – засорения сетки и ее разрыва.
В случае засорения сетки структурная схема надежности соответствует конструктивной. Последовательное соединение фильтров в этом случае только снизит надежность системы, так как отказ любого из фильтров приведет к отказу системы, поскольку необходимый поток жидкости не будет проходить сквозь фильтр.
Лекция 11
Оценка безопасности технических систем
Критерии безопасности ТС
Основным базовым показателем надёжности и безопасности технических систем может служить вероятность безотказной работы Р(t) – вероятность того, что в заданном интервале времени t = Т не возникнет отказа этого объекта.
Значение Р(t) может находиться в пределах 0 ≤ Р(t) ≤ 1. Вероятность безотказной работы Р(t) и вероятность отказа R(t) образуют полную группу событий, поэтому
P(t) + R(t) =1 .
Допустимое значение Р(t) выбирается в зависимости от степени опасности отказа объекта. Например, для ответственных изделий авиационной техники допустимые значения Р(t) = 0,9999 и выше, т.е. практически равны единице.
При высоких требованиях к надёжности объекта задаются допустимым значением Р(t) = γ% (γ% – вероятность безотказной работы объекта в %) и определяют время работы объекта t = Тγ, соответствующее данной регламентированной вероятности безотказной работы. Значение Тγ называется гамма-процентным ресурсом и по его значению судят о большей или меньшей безотказности и безопасности объектов.
Пусть R(t) – вероятность возникновения аварийной ситуации на отрезке времени [0, t]. Эта вероятность должна удовлетворять условию R(t*) ≤ R* ,
где R* – предельно допустимое (нормативное) значение риска возникновения аварийной ситуации. Используем нормативное значение вероятности безотказной, т.е. безопасной, работы Р*, которая весьма близка к единице (например, R* = 1).
Функция риска на отрезке времени [0, t ] дополняет функцию безопасности P(t) до единицы: R(t) =1- P(t) .
Интенсивность риска аварийной ситуации (удельный риск) аналогична интенсивности отказов:
r(t) = - P’(t) / P(t) = R’(t) / [1- R(t)] .
Поскольку уровень безопасности должен быть высоким, то можно принять
1- R(t) = P(t) » 1.
Тогда интенсивность риска аварийной ситуации будет r(t) » R’(t) = - P’(t).
Поскольку время t при оценке риска аварии исчисляют в годах, то r(t) имеет смысл годового риска возникновения аварийной ситуации. Средний годовой риск аварии: rср (t) = R(t) /T .
Пусть, например, rср = const = 10–5 год–1; Т = 50 лет. Тогда
R (T ) = r (t)T = 10-5 * 50 = 5* 10-4;
P(T) =1- R(T) =1- 5 ×10-4 = 0,9995 .
Для одинаковых технических объектов функция безопасности Pn (t) = Pn (t)
где n – численность парка одинаковых объектов. В этом случае функция
риска
Rn (t) = 1- [1- R(t) ]n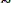 
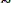nR(t) , при условии n R (t) << 1.
Аналогично для удельного риска: rn (t)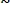 
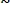n r (t) и rn ср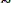 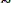n r ср (t) .
Инженерные расчёты инженерных конструкций на безопасность основаны на концепции коэффициентов запаса. В этом случае расчётное условие имеет вид
F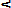 
S /m ,
где F – параметр воздействия; S – параметр сопротивления; m – коэффициент безопасности (m > 1).
Дата: 2019-02-25, просмотров: 384.
