В практике решения большого числа задач формула полной вероятности (ФПВ) и формула Байеса, являющиеся следствием основных теорем, находят широкое применение.
Формула полной вероятности.
Если по результатам опыта можно сделать n исключающих друг друга предположений (гипотез) H1, H2, … Hn, представляющих полную группу несовместных событий (для которой…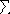 
), то вероятность события А, которое может появиться только с одной из этих гипотез, определяется:
P(A) = P(Hi ) P(A|Hi ), (19)
где P(Hi) – вероятность гипотезы Hi; P(А| Hi) – условная вероятность
события А при гипотезе Hi.
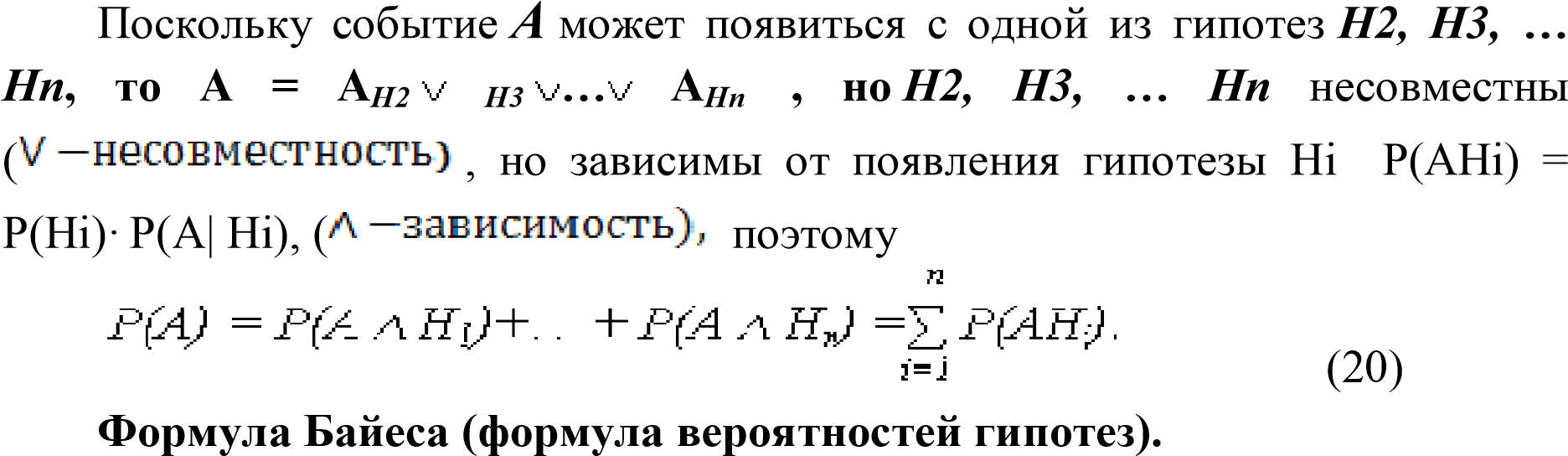
Если до опыта вероятности гипотез H1, H2, … Hn были равны P(H1), P(H2), …, P(Hn), а в результате опыта произошло событие А, то новые (условные) вероятности гипотез вычисляются:
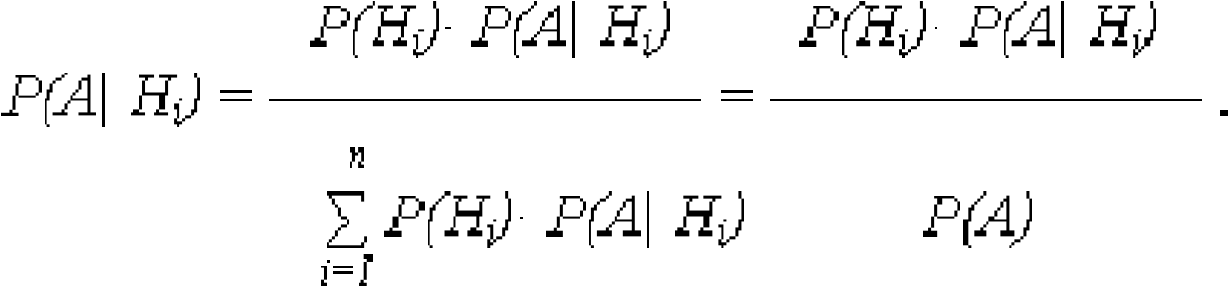(21)
Доопытные (первоначальные) вероятности гипотез P(H1), P(H2), …, P(Hn) называются априорными, а послеопытные - P(H1| А), … P(Hn| А) – апостериорными.
Формула Байеса позволяет «пересмотреть» возможности гипотез с учетом полученного результата опыта.
Доказательство формулы Байеса следует из предшествующего материала. Поскольку P(Hi А) = P(Hi)*А| Hi) = P(Hi)*P(Hi| А): откуда, с учетом (21), получается выражение 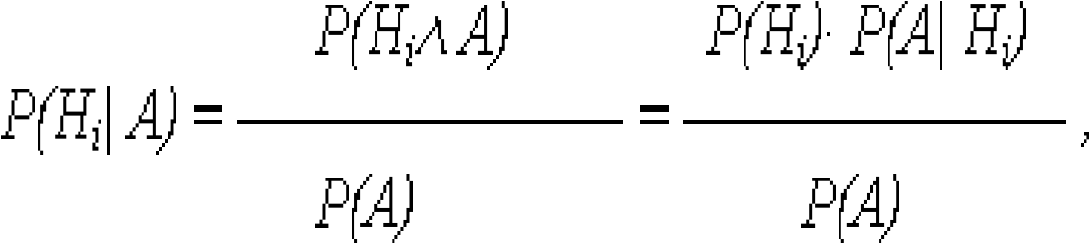(22).
(22)
Если после опыта, давшего событие А, проводится еще один опыт, в результате которого может произойти или нет событие А1, то условная вероятность этого последнего события вычисляется по (21), в которую входят не прежние вероятности гипотез P(Hi), а новые - P(Hi| А):
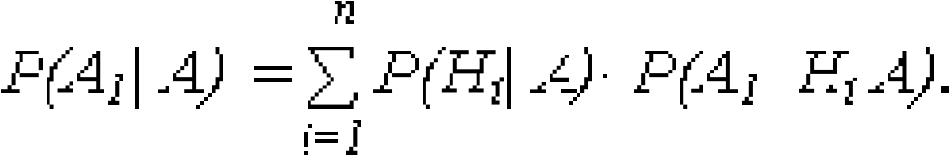(23)
Выражение (23) называют формулой для вероятностей будущих событий.
Лекция 6
Показатели надежности невосстанавливаемых
Объектов
Общие положения
Невосстанавливаемым называют такой элемент (объект), который (которое) после работы до первого отказа заменяют на такой же элемент (объект), так как его восстановление в условиях эксплуатации невозможно. В качестве примеров невосстанавливаемых элементов можно назвать диоды, конденсаторы, триоды, микросхемы, гидроклапаны, пиропатроны и т.п. [1 ,
5].
Наиболее важные показатели надёжности невосстанавливаемых объектов – показатели безотказности, к которым относятся:
• вероятность безотказной работы;
• плотность распределения отказов;
• интенсивность отказов;
• средняя наработка до отказа.
Показатели надёжности представляются в двух вариантах:
- статистический (выборочные оценки) ; - вероятностный.
Статистические выборочные оценки показателей получаются по результатам испытаний на надёжность.
Например, в ходе испытаний какого-то числа однотипных объектов получено конечное число интересующего нас параметра – наработки до отказа. Полученные числа представляют собой выборку некоего объёма из общей «генеральной совокупности», имеющей неограниченный объём данных о наработке до отказа объекта.
Количественные показатели, определённые для «генеральной совокупности», являются истинными, достоверными (вероятностными) показателями, поскольку объективно характеризуют случайную величину – наработку до отказа.
Показатели, определённые для выборки, и, позволяющие сделать какието выводы о случайной величине, являются выборочными (статистическими) оценками. Очевидно, что при достаточно большом числе испытаний (большой выборке) оценки приближаются от вероятностных к истинным показателям.
Вероятностная форма представления показателей удобна при аналитических расчётах, а статистическая – при экспериментальном исследовании надёжности.
6.2. Показатели надежности невосстанавливаемого объекта (элемента)
Пусть время работы невосстанавливаемого элемента представляет собой случайную величину τ. В момент времени t = 0 элемент начинает работать, а в момент t = τ происходит его отказ, следовательно, τ является временем жизни элемента[2, 3, 5]. Таким образом, τ имеет случайный характер, и в качестве основного показателя надежности элемента можно назвать
функцию распределения, которая выражается зависимостью вида
F(t) = P(τ<t) . (6.1)
Функцию F(t) называют также вероятностью отказа элемента до момента t. Если элемент работает в течение времени t непрерывно, то существует непрерывная плотность вероятности отказа
f (t ) = dF t (t) / dt 6.2)
Следующим показателем надежности является вероятность безотказной работы за заданное время t или функция надежности, которая является
функцией, обратной функции распределения
P(t) = 1- F(t) = P(τ > t) . (6.3)
Графически функция надежности представляет собой монотонно убывающую кривую (рис. 6.1; при t=0 P(t =0)=l; при t →∞ P(t =∞)=0).
В общем виде вероятность безотказной работы испытуемых элементов конструкций определяется как отношение числа элементов оставшихся испрпытания к начальному числу элементов поставленных на испытание:
P(t) = (N - n)/N, (6.4)
где N - начальное число испытуемых элементов; п - число отказавших элементов за t; n0 = N - п - x – число изделий сохранивших работоспособность.
Важнейшим показателем невосстанавливаемого элемента является среднее время безотказной работы (Т0), которое определяют как
математическое ожидание случайной величины
∞
Т0 = M [τ] = ∫ tf (t) dt. (6.5) 0
После преобразования:
∞ ∞ ∞ ∞
T0 = ∫ t f (t) dt = - t P(t)│+ ∫ P(t) dt = ∫ P(t) dt. (6.6)
0 0 0 0
Среднее время безотказной работы и среднюю наработку до отказа можно получить по результатам испытаний. Для этого нужно проводить испытания до тех пор, пока не откажет последний из элементов. Пусть время жизни каждого из элементов соответственно равно τ1, τ2, ... , τ3. Тогда средняя наработка до отказа
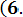
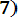
Т0 = (τ1 + τ2 + … + τn) / N = (1/N ) 
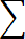
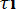
- число элементов, сохранивших работоспособность.
Величина P(t) и вероятность появления отказа F в момент времени t связаны соотношением
P(t) + F(t) = 1 , (6.8)
откуда
F(t) = 1 – P(t) (6.9) или
F(t) = 1 – n0/N. (6.10)
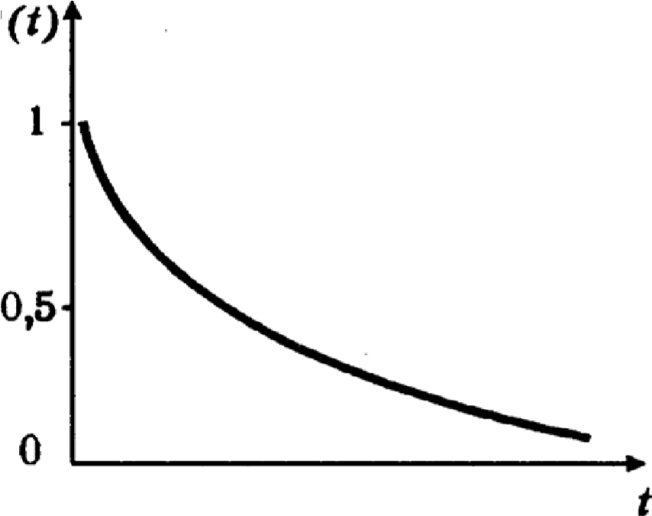
Рис. 6.1.Кривая функции надежности
Так как практически невозможно осуществить испытания всех элементов до отказа, то при большом значении п среднюю наработку до отказа можно определить по формуле
Т0 =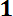 
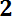
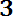
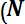
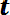
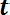
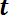
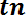
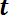
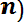
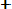
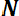
, (6.11)
где n — число отказавших элементов, N — число элементов, поставленных на испытания.
Следующей характеристикой надёжности невосстанавливаемого
элемента является интенсивность отказов, или опасность отказа, которая определяет надёжность элемента в каждый данный момент времени. Интенсивность отказа находят по формуле
l(t) = f (t) / P(t) = -[ dP(t) / dt] / P(t) = -P`(t) / P(t ) . (6.12)
Вероятность безотказной работы в интервале (t1, t2) выражается зависимостью
Р(t) = exp {-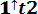 
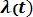
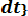
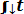
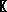
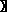
(6.13).
Функция λ(t) может быть определена по результатам испытаний.
Статистическая интенсивность отказов λ(t) равна отношению числа отказов, происшедших в единицу времени, к общему числу неотказавших элементов к этому моменту времени.
Многочисленные опытные данные показывают, что для многих элементов функция λ(t) имеет корытообразный вид (рис. 2).
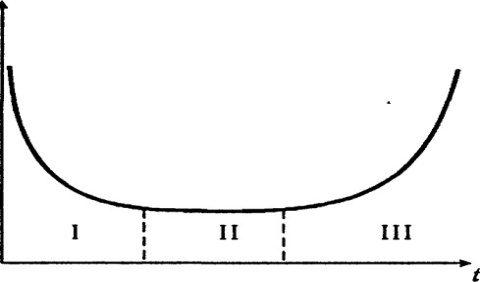
Рис. 2. Кривая интенсивности отказов во времени
Анализ графика показывает, что время испытания можно условно разбить на три периода. В первом из них функция λ(t) имеет повышенные значения. Это период приработки или период ранних отказов для скрытых дефектов. Второй период называют периодом нормальной работы. Для этого периода характерна постоянная интенсивность отказов. Последний, третий период — это период старения. Так как период нормальной работы является основным, то в расчетах надежности принимается λ(t) = λ = const. В этом случае при экспоненциальном законе распределения функция надежности имеет вид:
Р(t) = exp(- λ t). (6.14)
Среднее время жизни соответственно равно:
∞
T0 = ∫ exp(-λ t) dt = 1/λ. (6.15)
0
Поэтому функцию надежности можно записать и так:
Р(t) = еxp(-t/T0). (6.16)
Если время работы элемента мало по сравнению со средним временем жизни, то можно использовать приближенную формулу
Р(t) ≈ 1 – t/T0. (6.17)
Среднее время безотказной работы (Т0) является важнейшим показателем невосстанавливаемого элемента, которое определяют как математическое ожидание случайной величины
∞
Т0 = M [τ] = ∫ tf (t) dt. (6.18) 0
После преобразования:
∞ ∞ ∞ ∞
T0 = ∫ t f (t) dt = - t P(t)│+ ∫ P(t) dt = ∫ P(t) dt. (6.19)
0 0 0 0
Среднее время безотказной работы и среднюю наработку до отказа можно получить по результатам испытаний. Для этого нужно проводить испытания до тех пор, пока не откажет последний из элементов. Пусть время жизни каждого из элементов соответственно равно τ1, τ2, ... , τ3. Тогда средняя наработка до отказа
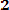
Т0 = (τ1 + τ2 + … + τn) / N = (1/N )
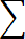
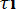
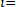
Если испытаниям подвергают N элементов и τ1, τ2,…τN —время их жизни, то статистическую дисперсию находят из выражения
N
S 2 = 1/(N – 1) Σ (τ i - τ )2, (6.21) i=1 где τ = (1/N) Στi.
На практике в качестве оценки надежности чаще используют среднее квадратическое отклонение (σ), которое определяют как корень квадратный из дисперсии:
σ[τ]=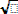 
(D[τ])2.
Пример 6.1. На испытания поставлено N =100 элементов. Испытания проводились в течение t = 200 ч. В процессе проведения испытаний отказало n = 5 элементов, при этом отказы зафиксированы в следующие моменты:
τ1 = 50 ч; τ2 = 80 ч; τ3 = 90ч; τ4 = 100 ч; τ5 = 150 ч;
остальные элементы не отказали. Определить среднюю наработку до
отказа Т0.
Решение. Для решения задачи воспользуемся формулой () T0 =[(50+80+90+100+150)+(100-5)200]/100 =194.7 ч. Ответ: T0 = 194.7ч.
Вероятность безотказной работы в интервале (t1, t2) выражается зависимостью
T 2
P(t) = exp{- ∫ λ(t) dt} (6.22) t 1
Функция λ(t) может быть определена по результатам испытаний. Предположим, что испытаниям подвергают N элементов. Пусть n(t) — число элементов, не отказавших к моменту t. Тогда при достаточно малом Δt и достаточно большом N получим
λ(t) = Δn/[Δt n(t)], (6.23) где Δn — число отказов на участке Δt.
Пример 6.2. По данным эксплуатации генератора установлено, что наработка до отказа подчиняется экспоненциальному закону с параметром λ = 2.10-5 1/час.
Найти вероятность безотказной работы за время t = 100 часов.
Определить математическое ожидание наработки до отказа. Решение.
Определим вероятность безотказной работы по формуле:
P(t) = e- λ t = exp(-2.10-5.100) = 0,998.
Математическое ожидание наработки до отказа определяем по формуле :
M0 = 1/λ = 1/(2.10-5) = 5.104 ч.
Ответ: P(t) = 0,998; M0 = 5.104 ч.
Пример 6.3. Построить кривую интенсивности отказов по данным табл. На испытания поставлено N элементов (N = 200), испытания проводились в течение t = 100 ч.
Таблица 6.1.
Результаты испытаний элемента (к примеру 6.3.)
| № п/п | Δt, ч | Δn | n(t) | № п/п | Δt, ч | Δn | n(t) |
| 1 2 3 4 5 | 0-10 10-20 20-30 30-40 40-50 | 10 8 6 4 2 | 190 182 176 172 170 | 6 7 8 9 10 | 50-60 60-70 70-80 80-90 90-100 | 2 2 4 5 8 | 168 166 162 157 149 |
Обозначения: Δt — интервал испытаний; Δn — число отказов; n(t) — число неотказавших элементов.
Для построения кривой (рис.) вычислим интенсивность отказов λ(ti) ч-1 по формуле
(6.25): λ(t1) = 10/(10.190) = 0,0052; λ(t2) = 8/(10.182) = 0,0044; λ(t3) = 6/(10.176) = 0,0034; λ(t4) = 4/(10.172) = 0,0023; λ(t5) = 2/(10.170) = 0,0011; λ(t6) = 2/(10.168) = 0,0011; λ(t7) = 2/(10.166) = 0,0012; λ(t8) = 4/(10.162) = 0,0024; λ(t9) = 5/(10.157) = 0,0032; λ(t10) = 8/(10.149) = 0,0053.
λ(t)10-3, ч-1
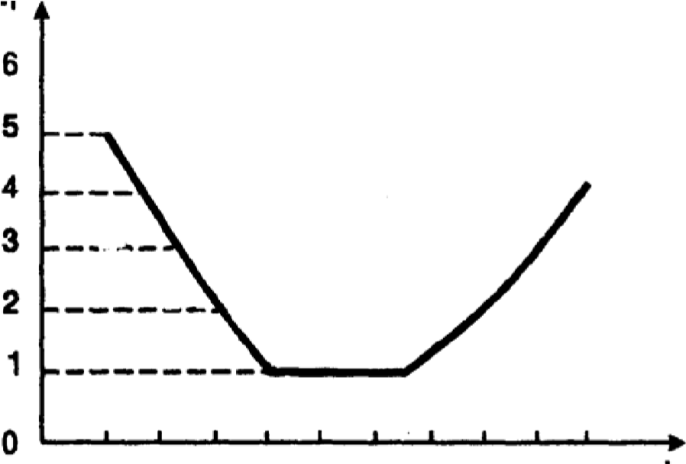
20 40 60 80 100 t, ч
Рис. Кривая интенсивности отказов во времени
Дата: 2019-02-25, просмотров: 321.
