Нормальный закон распределения часто называют законом Гаусса. Этот закон играет важную роль и наиболее часто используется на практике по сравнению с другими законами распределения.
Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. В теории надёжности его используют для описания постепенных отказов, когда распределение времени безотказной работы вначале имеет низкую плотность, затем максимальную и далее плотность снижается.
Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие, примерно равнозначные факторы.
Нормальный закон распределения описывается следующей зависимостью:
f (x) =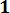 
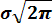
exp {– (x-m) / 2 σ2}, (3.7)
где е = 2,71828 – основание натурального логарифма; π= 3 ,14159;
т и σ –параметры распределения, определяемые по результатам
испытаний; Х – случайная величина.
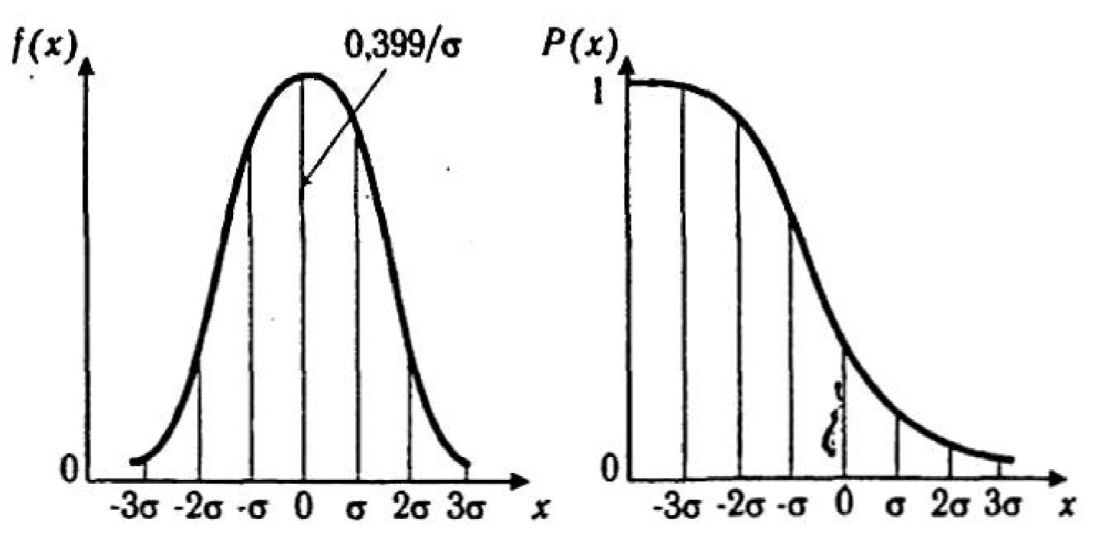
Кривая плотности распределения приведена на рис. 3.2.
а б
Рис. 3.2. Кривые плотности вероятности (а) и функции надежности
(б) нормального распределения
Параметр т = Мx представляет собой среднее значение случайной величины X, оцениваемое по формуле
Мх =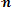 
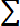
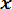
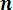
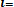
. (3.8)
параметр σ – среднее квадратическое отклонение случайной величины X, оцениваемое по формуле
____________________
s = √ {1/( n-1) -
Mx) . (3.9)
Интегральная функция распределения имеет вид
x
F (x) =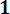 
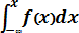
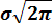
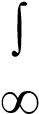exp {– (x-m)2 / 2σ 2 } dx, (3.10)
-
вероятность отказа и вероятность безотказной работы соответственно Q (x) =F(x), Р(х) =1 -F(x).
Вычисление интегралов заменяют использованием таблиц нормального распределения, при котором Мx = 0 и σ = 1. Для этого распределения функция плотности вероятности имеет одну переменную t и выражается зависимостью.
f0 (t) =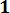 
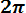exp(-t2/2), (3.11)
Величина t является центрированной (так как Мt = 0) и нормированной (так как σt = 1).
Функция распределения (функция Лапласа) соответственно запишется в виде:
t
F
| 0 |
| ( |
| = |
| t) |
| ∫ |
-∞
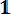
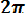
Из этого уравнения следует, что F0 (t )+ F0 (-t) = 1 или F (t)= 1 - F0 ( t ).
При использовании табл. 1 приложения [4] следует в формулу (3.13) вместо t подставить
ее значение: t = (t – Mx)/σ, (3.13)
при этом t называют квантилью нормированного нормального распределения (обычно обозначают up).
Плотность распределения и вероятность отказа соответственно равны: f(x) = f0(t)/σ; Q (x)= F0 ( t );
тогда вероятность безотказной работы
Р(х) = l - F0(t), где f0(t) и F0(t), определяют по таблицам.
В табл. 1 П1 приложения [4] приведены значения Ф*(t) в зависимости от t = x = (t – Mx)/σ.
В работах по надежности часто вместо интегральной функции распределения F0(t) используют функцию Лапласа:
t
Ф
| *( |
| х |
| ) |
| = |
| ∫ |
-∞
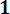
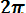
При этом,
F0(t) =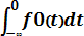 
| + |
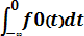= 0.5 + Ф*(t)
(3.15) Вероятности отказа и безотказной работы, выраженные через функцию Лапласса:
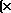
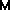
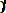
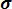
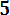
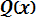
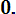
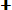
Ф*( , Р(х) = 0,5 - Ф*(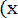 
,
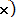
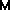
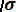
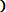
(3.16)
Вероятность попадания случайной величины Х в заданный интервал значений от α до β вычисляют по формуле
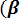
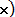
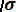
P (α < x < β) = Ф*( 
- Ф*(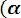 
.
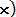
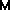
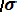
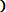
(3.17)
Пример 3.3. Определить вероятность безотказной работы P(t) в течение t = 2*104 ч подшипника скольжения, если ресурс по износу подчиняется нормальному закону распределения с параметрами
Mt = 4*104 ч, σ = 104 ч.
Р е ш е н и е. Находим квантиль
up=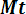 
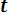
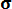= (2*104 – 4*104)/104 = - 2.
По табл. П.1приложения [4] определяем, что Р(t) =0,0228.
Пример 4.4. Пусть случайная величина Х представляет собой предел текучести стали. Опытные данные показывают, что предел текучести имеет нормальное распределение с параметрами M = 650 МПа, σ = 30 МПа. Найти вероятность того, что полученная плавка стали имеет предел текучести в интервале 600 — 670 МПа.
Р е ш е н и е. Для определения вероятности воспользуемся формулой (3.17)
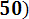
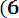
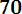
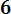
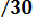
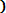
P (600< Х < 670) = Ф*( 
- Ф*(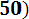 
=
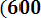
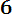
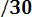
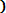
0.697.
Ответ: Р(Х) = 0,697.
Пример 3.5. Случайная величина X распределена по нормальному закону и представляет собой ошибку измерения датчика давления. При измерении датчик имеет систематическую ошибку в сторону завышения на 0,5 МПа, среднее квадратическое отклонние ошибки измерения составляет 0,2 МПа.
Найти вероятность того, что отклонение измеряемого значения от истинного не превзойдет по абсолютной величине 0,7 МПа.
Р е ш е н и е. По формуле (3.17) с использованием табл.П.1 приложения определим
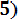
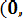
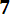
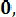
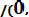
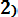
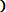
P (0,2< Х < 07) = Ф*( 
- Ф*(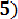 
=
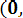
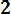
0,77.
Ответ: Р(Х) = 0,77.
Гамма-распределение
Гамма-распределение является двухпараметрическим распределением. Оно занимает важное место в теории надежности. Плотность распределения имеет ограничение с одной стороны (0 ≤ х ≤ ∞). Если параметр α формы кривой распределения принимает целое значение, то это свидетельствует о вероятности появления такого же числа событий (например, отказов) при условии, что они независимы и появляются с постоянной интенсивностью λ.
Гамма-распределение широко применяют при описании появления отказов стареющих элементов, времени восстановления, наработки на отказ резервированных систем. При различных параметрах гамма-распределение принимает разнообразные формы, что и объясняет его широкое применение.
Плотность вероятности гамма-распределения определяется равенствами
f(x) = [λα / Γ(α)]x α-1 e -λx , при x ≥0 ; (3.18)
f(x) = 0 при x <0 , где λ >0, α >0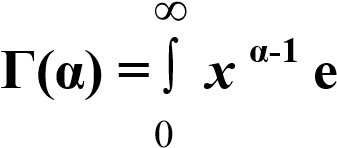 
-x dx. (3.19)
Кривая изменения плотности распределения приведена на рис. 4.5.
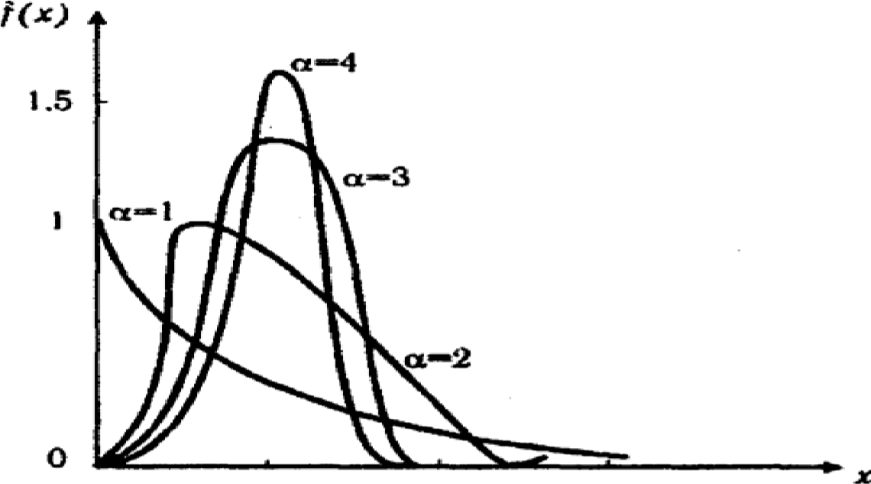
Рис. 4.3. Кривые плотности гамма-распределения
Функция распределения x
F(x)= λα / Г(α) ∫ x α-1 e -λx dx при x≥0; (3.20)
F(x) = 0 при х< 0.
Математическое ожидание и дисперсия соответственно равны:
Мx = α/λ; Dx = α/λ2 . (3.21)
При α <1 интенсивность отказов монотонно убывает (что соответствует периоду приработки изделия), при α >1 — возрастает (что характерно для периода изнашивания и старения элементов).
При α =1 гамма-распределение совпадает с экспоненциальным распределением, при α >10 гамма-распределение приближается к нормальному закону. Если α принимает значения произвольных целых положительных чисел, то такое гамма-распределение называют распределением Эрланга. Если λ =1/2, а значение α кратно 1/2, то гаммараспределение совпадает с распределением χ2 (хи-квадрат).
Лекция 4 Основные понятия надёжности. Классификация отказов. Составляющие надёжности.
Термины и определения, используемые в теории надёжности, регламентированные ГОСТ 27.002-89 «Надёжность в технике . Термины и определения».
Основные понятия
Надёжность – свойство объекта выполнять заданные функции, сохраняя во времени и в заданных пределах значения установленных эксплуатационных показателей.
Объект – техническое изделие определённого целевого назначения, рассматриваемое в периоды проектирования, производства, испытаний и эксплуатации.
Объектами могут быть различные системы и их элементы.
Элемент – простейшая составная часть изделия, в задачах надёжности может состоять из многих деталей.
Система – совокупность совместно действующих элементов, предназначенная самостоятельного выполнения заданных функций.
Понятия элемента и системы трансформируются в зависимости от поставленной задачи. Например, улевыемочный комбайн при установлении его собственной надёжности рассматривается как система, состоящая из отдельных элементов – механизмов, деталей и т.п., а при изучении надёжности технологической линии – как элемент.
Надёжность объекта характеризуется следующими основными состояниями и событиями.
Исправность – состояние объекта, при котором он соответствует всем требованиям, установленным нормативно-технической документацией (НТД).
Работоспособность – состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения основных параметров, установленных НТД.
Основные параметры характеризуют функционирование объекта при выполнении поставленных задач.
Понятие исправность шире, чем понятие работоспособность. Работоспособный объект обязан удовлетворять лишь тем требованиям НТД, выполнение которых обеспечивает нормальное применение объекта по назначению. Таким образом, если объект неработоспособен, то это свидетельствует о его неисправности. С другой стороны, если объект неисправен, то это не означает, что он неработоспособен.
Предельное состояние – это состояние объекта, при котором его применение по назначению недопустимо или нецелесообразно.
Применение (использование) объекта по назначению прекращается в следующих случаях:
- при неустранимом нарушении безопасности;
- при неустранимом отклонении величин от заданных параметров; - при недопустимом увеличении эксплуатационных расходов.
Для некоторых объектов предельное состояние является последним в его функционировании, т.е. объект снимается с эксплуатации, для других определённой фазой в эксплуатационном графике, требующей проведения ремонтно-восстановительных работ.
В связи с этим объекты могут быть:
- невосстанавливаемые, для которых работоспособность в случае возникновения отказа, не подлежит восстановлению;
- восстанавливаемые, работоспособность которых может быть восстановлена, в том числе и путём замены.
К числу невосстанавливаемых объектов можно отнести,
Например: подшипники качения, полупроводниковые изделия, зубчатые колёса и т.п. Объекты, состоящие из многих элементов, например, проходческий комбайн, ленточный конвейер, электронная аппаратура, являются восстанавливаемыми, поскольку их отказы связаны с повреждениями одного или немногих элементов, которые могут быть заменены.
В ряде случаев один и тот же объект в зависимости от особенностей, этапов эксплуатации или назначения может считаться восстанавливаемым или невосстанавливаемым.
Отказ – событие, заключающееся в нарушении работоспособности объекта. Критерий отказа – отличительный признак или совокупность признаков, согласно которым устанавливается факт возникновения отказа.
4.2. Классификация и характеристики отказов По типу отказы подразделяются на:
- отказы функционирования (выполнение основных функций объектом прекращается, например , поломка зубьев шестерни редуктора электродвигателя ленточного конвейера) ;
- отказы параметрические (некоторые параметры объекта изменяются в недопустимых пределах, например, потеря точности станка).
По природе отказы могут быть:
- случайные, обусловленные непредусмотренными перегрузками, дефектами материала, ошибками персонала или сбоями системы управления и т.п.;
- систематические, обусловленные закономерными и неизбежными явлениями, вызывающими постепенное накопление повреждений: усталость, износ, старение коррозия и т.п.
Основные признаки классификации отказов:
- характер возникновения;
- причина возникновения;
- характер устранения;
- последствия отказов;
- дальнейшее использование объекта;
- легкость обнаружения; - время возникновения.
Рассмотрим подробнее каждый из классификационных признаков:
| Характер возникновения | - внезапный отказ – отказ проявляющийся в резком (мгновенном) изменении характеристик объекта; |
- постепенный отказ – отказ, происходящий в резуль -
тате постепенного ухудшения качества объекта.
Внезапные отказы обычно проявляются в виде механических повреждений элементов (трещины – хрупкое разрушение, пробои изоляции, обрывы и т. п.) и не сопровождаются предварительными видимыми признаками их приближения. Внезапный отказ характеризуется независимостью момента наступления от времени предыдущей работы.
Постепенные отказы – связаны с износом деталей и старением материалов.
| Причина возникновения | - конструкционный отказ , вызванная недостатками и неудачной конструкцией объекта; - производственный отказ, связанный с ошибками при изготовлении объекта по причине несовершенства или нарушения технологии; - эксплуатационный отказ, вызванный нарушением правил эксплуатации. |
| Характер устранения и последствия отказов | - устойчивый отказ; - перемежающийся отказ (возникающий, исчезающий) , последствия отказа: лёгкий отказ (легкоустранимый) ; - средний отказ (не вызывающий отказы смежных узлов вторичные отказы) ; - тяжёлый отказ (вызывающий вторичные отказы или приводящий к угрозе жизни и здоровью человека). |
| Дальнейшее использование | - полные отказы, исключающие возможность работы объекта до их устранения; |
| объекта | - частичные отказы, при которых объект может частично использоваться; |
| Лёгкость | - очевидные (явные) отказы; |
| обнаружения | - скрытые (неявные) отказы. |
| Время возникновения | - приработанные отказы, возникающие в начальный период эксплуатации; |
- отказы при нормальной эксплуатации; - износовые отказы, вызванные необратимыми процессами износа деталей, старения материалов и пр.
Составляющие надёжности
Надёжность является комплексным свойством, включающем в себя в зависимости от назначения объекта или условий его эксплуатации ряд простых свойств:
- безотказность;
- долговечность;
- ремонтопригодность; - сохраняемость.
Безотказность – свойство объекта непрерывно сохранять работоспособность в течение некоторой наработки или в течение некоторого времени.
Наработка – продолжительность или объём работы объекта, измеряемая в любых неубывающих величинах (единица времени, число циклов нагружения, километры пробега и т.п.).
Долговечность – свойство объекта сохранять работоспособность до на ступления предельного состояния при установленной системе
технического обслуживания и ремонтов.
Ремонтопригодность – свойство объекта, заключающееся в его приспособленности к предупреждению и обнаружению причин возникновения отказов, поддержанию и восстановлению работоспособности путём проведения ремонтов и технического обслуживания.
Сохраняемость – свойство объекта непрерывно сохранять требуемые эксплуатационные показатели в течение (и после) срока хранения и транспортирования.
В зависимости от объекта надёжность может определяться всеми перечисленными свойствами или частью их. Например, надёжность колеса зубчатой передачи, подшипников определяется их долговечностью, а станка долговечностью, безотказностью и ремонтопригодностью.
Дата: 2019-02-25, просмотров: 314.
