Показатель надёжности количественно характеризует, в какой степени данному объекту присущи определённые свойства, обусловливающие надёжность. Одни показатели надёжности (технический ресурс, срок службы) могут иметь размерность, ряд других (вероятность безотказной работы, коэффициент готовности) являются безразмерными.
Рассмотрим показатели составляющей надёжности – долговечность.
Технический ресурс – наработка объекта от начала эксплуатации или возобновления эксплуатации после ремонта до наступления предельного состояния. Технический ресурс может быть регламентирован :
- до среднего, капитального , от капитального до ближайшего среднего ремонта и т.п. Если регламентация отсутствует, то имеется в виду ресурс от начала эксплуатации до достижения предельного состояния после всех видов ремонтов.
Для невосстанавливаемых объектов понятия технического ресурса и наработки до отказа совпадают.
Назначенный ресурс – суммарная наработка объекта, при достижения которой его эксплуатация должна быть прекращена независимо от его состояния.
Срок службы – календарная продолжительность эксплуатации
(хранение, ремонт и т.п.) от её начала до наступления предельного состояния.
На рис. Приведена графическая интерпретация перечисленных показателей, при этом:
t0 = 0 – начало эксплуатации; t1. t5 – моменты отключения по технологическим причинам;
t2, t4, t6, t8 – моменты включения объекта; t3, t7 – моменты вывода объекта в ремонт, соответственно, средний и капитальный; t9 – момент прекращения эксплуатации; t10 – момент отказа объекта.
Наработка
t0 = 0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10
Технический ресурс (наработка до отказа).
ТР = t1+ (t3 – t2) + (t5 – t4) + (t 7 – t6) + (t10 – t8).
Назначенный ресурс
ТН= t1+ (t3 – t2) + (t5 – t4) + (t 7 – t6) + (t9 – t8).
Срок службы объекта ТС = t10.
Для большинства технических объектов в качестве критерия долговечности чаще всего используется технический ресурс.
Лекция 5. Теория вероятностей в математических расчетах надёжности технических систем
Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях.
Основные понятия теории множеств
Одним из основных понятий является случайное событие.
Событием называется всякий факт (исход), который в результате опыта (испытания, эксперимента) может произойти или не произойти [9].
Каждому из таких событий соответствует определенное число – вероятность совершения этого события.
Теории вероятностей основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств.
Множество – это любая совокупность объектов произвольной природы. Каждый объект называется элементом этого множества.
Предположим, что производится некоторый опыт (эксперимент, испытание), результат которого заранее неизвестен, случаен [9]. Тогда множество 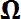 всех возможных исходов опыта представляет пространство элементарных событий, а каждый его элемент
всех возможных исходов опыта представляет пространство элементарных событий, а каждый его элемент 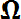
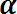
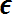 (α принадлежит множеству
(α принадлежит множеству 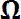 ) является элементарным событием. Любой набор элементарных событий (любое их сочетание) считается подмножеством
) является элементарным событием. Любой набор элементарных событий (любое их сочетание) считается подмножеством
(частью) множества 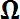 и является случайным событием, т. е. любое событие А – это подмножество множества
и является случайным событием, т. е. любое событие А – это подмножество множества 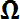 : А
: А 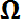
 (А является подмножеством
(А является подмножеством 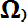 .
.
Множество А считается заданным, если указано характеристическое свойство элементов этого множества, т. е. такое свойство, которым обладают все элементы этого множества и только они. Одним из основных понятий множеств является понятие принадлежности элемента множеству.
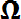
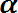
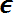
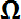
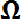

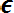

 В качестве обозначения того, что предмет α принадлежит множеству А, пишут . Если а принадлежит А (не принадлежит А) , то пишут ). Может случиться, что характеристическим свойством, определяющим множество А, не обладает вообще ни один предмет; тогда говорят, что множество А пустое и пишут А =
В качестве обозначения того, что предмет α принадлежит множеству А, пишут . Если а принадлежит А (не принадлежит А) , то пишут ). Может случиться, что характеристическим свойством, определяющим множество А, не обладает вообще ни один предмет; тогда говорят, что множество А пустое и пишут А = 















 . Например, множество действительных решений уравнения х2 = - 1 пустое. Если каждый элемент множества А является в то же время элементом множества В, то множество А называется подмножеством множества В и пишут А ]. Если одновременно выполнено А и В то говорят, что
. Например, множество действительных решений уравнения х2 = - 1 пустое. Если каждый элемент множества А является в то же время элементом множества В, то множество А называется подмножеством множества В и пишут А ]. Если одновременно выполнено А и В то говорят, что 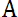
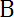
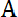
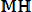
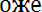

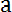
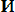
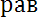

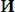
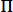
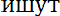


 В.
В.
.Объединением А множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В. Пересечением А множеств А и В называется множество, состоящее из всех элементов, принадлежащих как А, так и В. Операции объединения и пересечения коммутативны, ассоциативны и взаимно дистрибутивны.
Например, (А 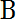
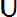
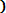
 С = (А
С = (А 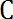
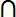
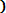
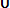 (В
(В  С) . Во многих разделах теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве X. Если Аподмножество X и Р- свойство, характеризующее элементы из А, то пишут
С) . Во многих разделах теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве X. Если Аподмножество X и Р- свойство, характеризующее элементы из А, то пишут
А= {х 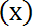
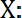

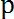
 - истина}. Например, если X- множество всех действительных чисел, а А - подмножество положительных чисел, то А=
- истина}. Например, если X- множество всех действительных чисел, а А - подмножество положительных чисел, то А=
{х 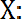

 }. . Если А , то множество х\А {х
}. . Если А , то множество х\А {х  Х: х
Х: х 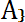

называется дополнением множества А . Операции объединения, пересечения и дополнения связаны т. н. законами де Моргана. Например, Х\(А 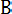
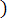

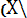
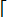
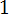
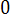
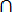

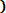
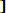
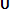




Событие А может появиться с одной из гипотез H2, H3, … Hn, т. е. А =
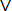
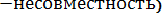
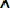
| Hn) = |
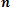

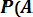





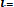

























 АH2 H3 … АHn , но H2, H3, … Hn несовместны ( , но зависимы от появления гипотезы Нi P(AHi) = P(Hi)*P(А| Hi)
АH2 H3 … АHn , но H2, H3, … Hn несовместны ( , но зависимы от появления гипотезы Нi P(AHi) = P(Hi)*P(А| Hi)

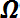 (
( 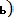
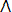
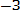
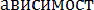

 поэтому P(A) = P(AHi)+…+ P(A
поэтому P(A) = P(AHi)+…+ P(A
В общем случае, если множествосодержит n элементов, то в нём можно выделить 2n подмножеств событий [9].
Раздел математики, который занимается исследованием операций над множествами (не только конечных, но и бесконечных операций), наз. алгеброй множеств. Алгебра множеств в свою очередь является частным случаем теории булевых алгебр.
Введём ряд определений.
Совместные (несовместные) события – такие события, появление одного из которых не исключает (исключает) возможности появления другого.
Зависимые (независимые) события – такие события, появление одного из которых влияет (не влияет) на появление другого события.
Противоположное событие относительно некоторого выбранного события А – событие, состоящее в не появлении этого выбранного события
(обозначается А).
Полная группа событий – такая совокупность событий, при которой в результате опыта должно произойти хотя бы одно из событий этой совокупности. Очевидно, что события А и 
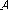
 составляют полную группу событий.
составляют полную группу событий.
Одна из причин применения теории множеств в теории вероятностей заключается в том, что для множеств определены важные преобразования, которые имеют простое геометрическое представление и облегчают понимание смысла этих преобразований. 5.2. Аксиомы теории вероятностей
Сопоставим каждому событию А число, называемое, как и прежде, его вероятностью и обозначаемое P(A) или P{A}. Вероятность выбирают так, чтобы она удовлетворяла следующим условиям или аксиомам:
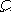














































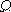
 P( ) = 1; P( ) = 0. (1)
P( ) = 1; P( ) = 0. (1)
P( ) P(A) P( ). (2)

























 Если Ai и Aj несовместные события, т. е. Ai
Если Ai и Aj несовместные события, т. е. Ai 






 Aj = ( - Аi несовместно с Аj), то пишем
Aj = ( - Аi несовместно с Аj), то пишем
P(Ai 







 Aj) = P(Ai) + P(Aj) (
Aj) = P(Ai) + P(Aj) ( 







 - не зависит) (3)
- не зависит) (3)
Приведенные аксиомы постулируются, и попытка доказать их лишена смысла. Единственным критерием справедливости является степень, с которой теория, построенная на их основе, отражает реальный мир.
Аксиому (3) можно обобщить на любое конечное число несовместных событий { Аi }n , i=1:








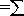
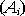
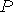
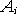
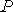















 (4)
(4)
С помощью аксиом можно вычислить вероятности любых событий (подмножеств пространства  ), используя вероятности элементарных событий. Вопрос о том, как определить вероятности элементарных событий, является риторическим. На практике они определяются либо из соображений, связанных с возможными исходами опыта (например, в случае бросания монеты естественно считать вероятности выпадения орла или решки одинаковыми), или на основе опытных данных (частот).
), используя вероятности элементарных событий. Вопрос о том, как определить вероятности элементарных событий, является риторическим. На практике они определяются либо из соображений, связанных с возможными исходами опыта (например, в случае бросания монеты естественно считать вероятности выпадения орла или решки одинаковыми), или на основе опытных данных (частот).
Последний подход широко распространен в прикладных инженерных задачах, поскольку позволяет косвенно соотнести результаты анализа с физической реальностью.
Предположим, что в опыте пространство можно представить в виде полной группы несовместных и равновозможных событий А1, А2, …, Аn. Согласно (3) их сумма представляет достоверное событие:



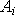








 =
= 
 ., (5)
., (5)
так как события А1, А2, …, Аn несовместны, то согласно аксиомам (1) и
(3):
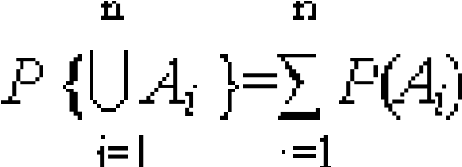 = P(
= P( 


 ) = 1. (6)
) = 1. (6)
Поскольку события А1, А2, …, Аn равновозможны, то вероятность каждого из них одинакова и равна
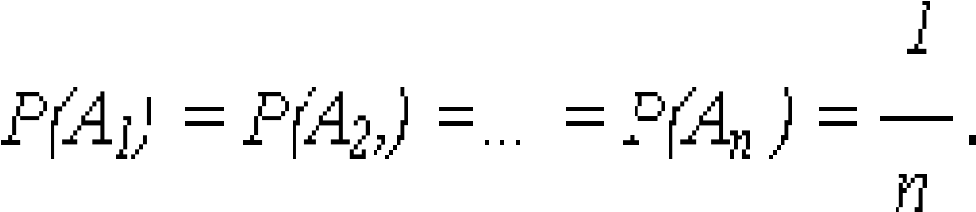
Отсюда непосредственно получается частотное определение вероятности любого события A:
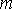

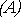
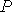






 (7)
(7)
как отношение числа случаев (mA), благоприятных появлению события
А, к общему числу случаев (возможному числу исходов опыта) n.
Совершенно очевидно, что частотная оценка вероятности есть не что иное как следствие аксиомы сложения вероятностей. Представив, что число n неограниченно возрастает, можно наблюдать явление, называемое статистическим упорядочением, когда частота события А все меньше изменяется и приближается к какому-то постоянному значению, которое и представляет вероятность события А.
Дата: 2019-02-25, просмотров: 358.