Для включения относящихся к этой игре заданий в уроки достаточно сделать на доске соответствующий чертеж. Ниже мы приводим серию постепенно усложняющихся чертежей, выполненных на основе одного и того же треугольника, к каждому из которых предлагается практически одинаковое задание-вопрос: «Сколько на чертеже многоугольников?»

После получения ответа и его проверки можно задавать более конкретные вопросы типа «Какие многоугольники есть на чертеже? Сколько на нем треугольников? Четырехугольников?» и т. д.

Основная цель работы с заданиями – выработка способа поиска ответа не хаотически, а с использованием постепенно формирующейся системы.

Планомерное включение заданий этого вида дает возможность продвигать детей в умении анализировать и синтезировать объекты, рассматривать их с различной точки зрения, соотносить производимые действия и их результаты; продвигает в умении обобщать результаты наблюдений; расширяет математический кругозор; помогает формировать связную грамотную речь, включающую математическую терминологию.

Раскроем основные направления работы с заданиями этого вида на примере первых двух чертежей.

В результате работы с первым чертежом дети должны найти на нем 3 треугольника, однако часто бывает так, что основной большой треугольник теряется, то есть чертеж расчленяется на составные части, а синтезировать из этих частей фигуру ученики еще не могут. В этом случае учитель оказывает помощь, которая может, например, заключаться в том, что чертеж воспроизводится на глазах детей: сначала возникает треугольник, а затем в нем проводится отрезок.

Возможно и использование особого, заготовленного заранее пособия такого вида: из картона вырезается треугольник-основа, на нее сверху накладываются треугольники разного цвета, которые получились при проведении отрезка, и прикрепляются к основе так, чтобы их можно было отогнуть, сверху накладывается бумажный треугольник, на котором воспроизведен чертеж. Этот треугольник тоже должен отгибаться. Если дети не находят решения, верхний треугольник отгибается, и становятся видны 2 треугольника, на которые разделен основной треугольник. Когда эти треугольники тоже отгибаются, появляется нерасчлененный основной треугольник, который и является третьим.

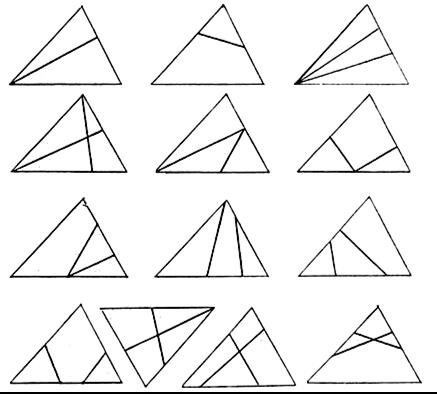
Работа со вторым чертежом строится так же, после чего необходимо рассмотреть оба чертежа вместе, сравнить их друг с другом и установить причину, которая привела к разнице решений (на первом чертеже 3 треугольника, на втором – 2 треугольника и четырехугольник).

Следующий шаг – создание своих чертежей, на которых тоже получается 3 треугольника или 2 треугольника и четырехугольник, а затем общий вывод о том, как в том и другом случае должен располагаться отрезок внутри треугольника (если он соединяет вершину треугольника и любую точку противоположной стороны, получается 3 треугольника, если любые точки двух сторон, которые не являются вершинами, получаем 2 треугольника и четырехугольник).

Развитие этого вида заданий может происходить за счет увеличения числа отрезков, проведенных внутри треугольника, а также за счет использования других многоугольников, имеющих большее число углов.

ЛИТЕРАТУРА

1. Истомина, Н. Б. Наглядная геометрия для 2 класса / Н. Б. Истомина. – М.: Линка-Пресс, 2002.

2. Истомина, Н. Б. Учимся решать комбинаторные задачи / Н. Б. Истомина, Е. П. Виноградова. – Смоленск: Ассоциация XXI век, 2004.

3. Кравченко, В. С. Устные упражнения по математике в 1–3 классах / В. С. Кравченко. – М.: Просвещение, 1979.

4. Рудницкая, В. М. Математика. 2 кл.: учеб. для учащихся общеобразоват. учр.: в 2 ч. / В. М. Рудницкая, Т. В. Юдачева. – М.: Вентана-Граф, 2008.

5. Рудницкая, В. М. Математика: рабочая тетрадь для 2 класса: № 1, 2 / В. М. Рудницкая, Т. В. Юдачева. – М.: Вентана-Граф, 2008.

6. Рудницкая, В. Н. Математика. 2 кл.: методика обучения / В. М. Рудницкая, Т. В. Юдачева. – М.: Вентана-Граф, 2006.

7. Энциклопедический словарь юного математика / сост. Н. П. Ернылев. – М.: Педагогика, 1980.