1. Работа по учебнику.
Задание № 12 (с. 78).
– Рассмотрите выражения.
– Чем они похожи? Чем отличаются?
– Как выполнить арифметические действия в выражениях со скобками?
– Вычислите их значения.
Запись: (90 – 45) + 45 = 90 90 – (45 + 15) = 30 и т. д.
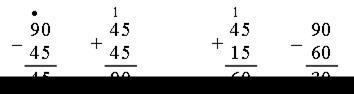
Задание № 13 (с. 78).
– Прочитайте условие задачи. Что известно?
– Запишите кратко условие задачи.
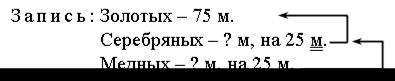
– Сформулируйте вопрос и решите задачу.
К условию, данному в задании, можно придумать много различных вопросов. Например: сколько серебряных монет было в кладе? Сколько медных монет было в кладе? Сколько всего было монет? На сколько медных монет было меньше, чем золотых? Сколько всего было золотых и серебряных монет? На сколько золотых и серебряных монет было больше, чем медных?
Разберите как можно больше вариантов задач. А завершить работу следует сравнением всех рассмотренных задач и способов их решения.
Задание № 16 (с. 79).
Задание следует рассматривать как подготовительное к изучению ряда последующих тем, посвященных табличным случаям умножения и деления.
Напомните учащимся известные им способы выполнения умножения.
Первый способ – пересчет элементов прямоугольной таблицы, составленной из фишек.
Например, 3 умножить на 2 – это 2 раза по 3.
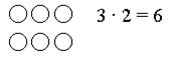
Второй способ – использование действия сложения.
Например, 5 умножить на 4 – значит, число 5 повторить слагаемым 4 раза, то есть:
5 + 5 = 10,
10 + 5 = 15,
15 + 5 = 20.
Следовательно, 5 · 4 = 20.
Задание № 14 (с. 79).
Задание выполняется с помощью портновского метра. Необходимо продемонстрировать ученикам, как правильно производить измерения.
2. Работа в печатной тетради № 1.
Задание № 116.
Наиболее сложный из всех случаев – № 3. Некоторым учащимся может показаться, что общей частью двух касающихся окружностей является дуга или отрезок, поэтому необходимо обратить внимание учащихся на то, что пересечением двух окружностей в данном случае является точка.
А – точка пересечения окружностей.
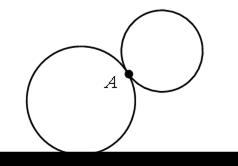
В первом случае две точки пересечения – В и С.
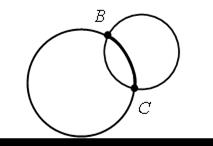
Во втором случае окружности пересекаются – имеют общий центр.
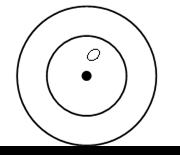
Задание № 117.
Выполняя задание, учащиеся наверняка столкнутся с ситуацией, когда длину того или иного пальца невозможно указать только в сантиметрах. А с более мелкой единицей длины (миллиметром) они еще не знакомы. Учитель советует использовать в этом случае слова «примерно», «около», «больше … , но меньше … », которые указывают на приближенные значения полученного результата.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки окружности.
– Назовите признаки многоугольника.
Домашнее задание: № 15 (учебник); № 118 (рабочая тетрадь).
Урок 41
Контрольная работа по теме «Сложение
и вычитание чисел в пределах 100»
Цели урока : проверить вычислительные навыки сложения и вычитания чисел в пределах 100; умение находить периметр любого многоугольника; умение строить окружность с помощью циркуля; умение решать составные задачи.
I вариант
1. Запишите цифрами:
| 4 дес. 5 ед. | 7 дес. 2 ед. |
| 8 дес. | 5 дес. |
| 9 дес. 2 ед. | 4 дес. 3 ед. |
2. Выполните действия:

3. У Тамары было 100 р. Она купила пачку чая за 35 р. и батон хлеба за 18 р. Сколько денег у нее осталось?
4. Вставьте пропущенные числа так, чтобы равенства были верными:
| 2 дм = см | 120 см = м см |
| 1 м = см | 45 см = дм см |
5. Вычислите периметр многоугольника.
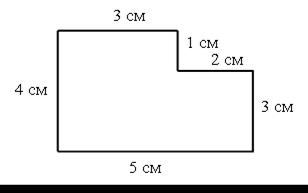
6. Постройте первую окружность с радиусом 4 см, а другую – с радиусом на 2 см больше. Отметьте точкой О центр окружности.
II вариант
1. Запишите цифрами:
| 2 дес. 9 ед. | 8 дес. 1 ед. |
| 4 дес. | 6 дес. |
| 7 дес. 8 ед. | 5 дес. 7 ед. |
2. Выполните действия:

3. В ларьке было 100 кг капусты. Продали 54 кг капусты, а привезли еще 45 кг. Сколько килограммов капусты стало в ларьке?
4. Вставьте пропущенные числа так, чтобы равенства были верными:
| 4 дм = см | 160 см = м см |
| 1 м = см | 76 см = дм см |
5. Вычислите периметр многоугольника.
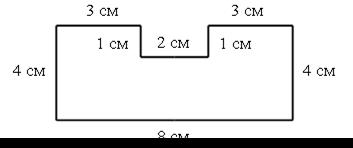
6. Постройте первую окружность с радиусом 5 см, а другую – с радиусом на 1 см меньше. Отметьте точкой О центр окружности.
Урок 42
Работа над ошибками. Решение задач
Цели урока : провести анализ выполненной контрольной работы; совершенствовать умение решать задачи; развивать умение рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Геометрическое задание.
Часто знает и дошкольник,
Что такое треугольник.
А уж вам-то как не знать?
Но совсем другое дело –
Быстро, точно и умело
Треугольники считать.
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И по краю, и внутри.
– Сосчитайте, сколько треугольников.
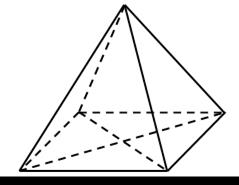
2. Задача на смекалку.
Из 25 учеников в классе 17 изучают английский язык, а 15 – французский. Сколько детей изучают оба языка?
Комментарий. Желательно иллюстрировать решение схемой, в которой круг слева означает детей, изучающих английский язык, а круг справа – французский. В пересечении кругов – дети, изучающие оба языка.
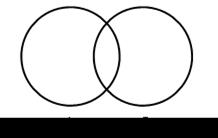
Схема дополняется в процессе решения задачи.
– Сколько ребят не изучают французский язык (изучают только английский)? (25 – 15 = 10.)
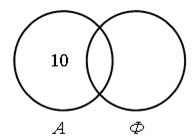
– Сколько человек изучают только французский язык (не изучают английский)? (25 – 17 = 8.)
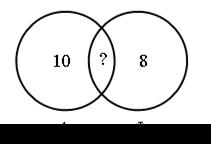
– Сколько человек изучают только один язык? (10 + 8 = 18.)
– Сколько человек изучают оба языка? (25 – 18 = 7.)
Дата: 2018-12-28, просмотров: 641.