Для того чтобы оценить и измерить количество информации в соответствии с вышеизложенными аспектами, применяются различные подходы. Среди них выделяются статистический, семантический, прагматический и структурный. Исторически наибольшее развитие получил статистический подход.

Статистический подход изучается в разделе кибернетики, называемом теорией информации. Его основоположником считается К. Шеннон, опубликовавший в 1948 г. свою математическую теорию связи. Большой вклад в теорию информации до него внесли ученые Х. Найквист и Хартли.

К. Шенноном было введено понятие количество информации как меры неопределенности состояния системы, снимаемой при получении информации. Количественно выраженная неопределенность состояния получила название энтропии по аналогии с подобным понятием в статистической механике. При получении информации уменьшается неопределенность, т.е. энтропия, системы. Очевидно, что чем больше информации получает наблюдатель, тем больше снимается неопределенность, и энтропия системы уменьшается. При энтропии, равной нулю, о системе имеется полная информации, и наблюдателю она представляется целиком упорядоченной.

До получения информации ее получатель мог иметь некоторые предварительные (априорные) сведения о системе X. Оставшаяся неосведомленность и является для него мерой неопределенности состояния (энтропией) системы. Обозначим априорную энтропию системы X через H ( X ). После получения некоторого сообщения наблюдатель приобрел дополнительную информацию I ( X ), уменьшившую его начальную неосведомленность так, что апостериорная (после получения информации) неопределенность состояния системы стала H ^* ( X ). Тогда количество информации I может быть определено как

.

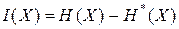Другими словами, количество информации измеряется уменьшением (изменением) неопределенности состояния системы.

Если апостериорная энтропия системы обратится в ноль, то первоначально неполное значение заменится полным знанием, и количество информации, полученной в этом случае наблюдателем, будет таково:

,

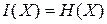т.е. энтропия системы может рассматриваться как мера недостающей информации.

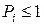Если система X обладает дискретным состоянием (т.е. переходит из состояния в состояние скачком), их количество равно N, а вероятность нахождения системы в каждом из состояний - P ₁, P ₂, ..., P_N, (причем  и ), то согласно теореме Шеннона энтропия системы H ( X ) равна:

.

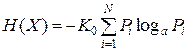Здесь коэффициент K ₀ и основание логарифма a определяют систему единиц измерения количества информации. Логарифмическая мера информации была предложена Хартли для представления технических параметров систем связи как наиболее удобная и более близкая к восприятию человеком, привыкшим к линейным сравнениям с принятыми эталонами. Знак "минус" перед коэффициентом K ₀ поставлен для того, чтобы значение энтропии было положительным, т.к. 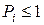, и логарифм в этом случае отрицательный.

Если все состояния системы равновероятны, т.е. 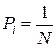, ее энтропия рассчитывается по формуле:

.

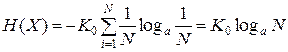Энтропия H обладает рядом свойств; укажем два из них:

1) H = 0 только тогда, когда все вероятности P_i, кроме одной, равны нулю, а эта единственная вероятность равна единице. Таким образом,        H = 0 только в случае полной определенности состояния системы;

2) при заданном числе состояний системы N величина H максимальна и равна 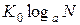, когда все P_i равны.

Определим единицы измерения количества информации с помощью выражения для энтропии системы с равновероятностными состояниями.

Пусть система имеет два равновероятностных состояния, т.е. N=2. Будем считать, что снятие неопределенности о состоянии такой системы дает одну единицу информации, так как при полном снятии неопределенности энтропия количественно равна информации H = I. Тогда

.

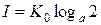Очевидно, что правая часть равенства будет тождественно равна единице информации, если принять K ₀ = 1 и основание логарифма a = 2. В общем случае при N равновероятностных состояний количество информации будет таково:

.

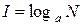Эта формула получила название формулы Хартли и показывает, что количество информации, необходимое для снятия неопределенности о системе с равновероятностными состояниями, зависит лишь от количества этих состояний.

Информация о состояниях системы передается получателю в виде сообщений, которые могут быть представлены в различной синтаксической форме, например, в виде кодовых комбинаций, использующих m различных символов и n разрядов, в каждом из которых может находиться любой из символов. Если код не избыточен, то каждая кодовая комбинация отображает одно из состояний системы. Количество кодовых комбинаций будет .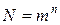

Подставив это выражение в формулу для I, получим: .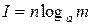

Если код двоичный, т.е. используются лишь два символа (0 и 1), то   m = 2 и I = n.

В этом случае количество информации в сообщении составит n двоичных единиц. Эти единицы называют битами (от англ. Binary digit (bit) – двоичная цифра).

При использовании в качестве основания логарифма числа 10 единицы измерения информации могут быть десятичными, или дитами. Так как 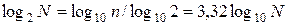, то десятичная единица составляет примерно 3,33 бита.

Иногда удобно применять натуральное основание логарифма e. В этом случае получающиеся единицы информации называются натуральными, или натами. Переход от основания a к основанию b требует лишь умножения на .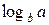

Введенная количественная статистическая мера информации широко используется в теории информации для оценки собственной, взаимной, условной и других видов информации. Рассмотрим в качестве примера собственную информацию. Под собственной информацией будем понимать информацию, содержащуюся в данном конкретном сообщении, а конкретное сообщение, как указывалось, дает получателю информацию о возможности существования конкретного состояния системы. Тогда количество собственной информации, содержащейся в сообщении X_i, определяется как

.

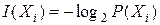Собственная информация обладает следующими свойствами:

1) собственная информация неотрицательна;

2) чем меньше вероятность возникновения сообщения, тем больше информации оно содержит. Именно поэтому неожиданные сообщения так воздействуют на психику человека, что содержащееся в них большое количество информации создает информационный психологический удар, иногда приводящий к трагическим последствиям;

3) если сообщение имеет вероятность возникновения, равную единице, то информация, содержащаяся в нем, равна нулю, так как заранее известно, что может прийти только это сообщение, а значит, ничего нового потребитель информации не получает;

4) собственной информации присуще свойство аддитивности, т.е. количество собственной информации нескольких независимых сообщений равно сумме собственной информации сообщений. Например, для собственной информации двух сообщений X_i и Y_i может быть записано:

.

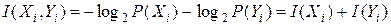Следует еще раз отметить, что статистический подход к количественной оценке информации был рассмотрен для дискретных систем, случайным образом переходящих из состояния в состояние, и, следовательно, сообщение об этих состояниях также возникает случайным образом. Кроме того, статистический метод определения количества информации практически не учитывает семантического и прагматического аспектов информации.

Семантический подход определения количества информации является наиболее трудно формализуемым и до сих пор окончательно не определившимся.

Наибольшее признание для измерения смыслового содержания информации получила тезаурусная мера, предложенная Ю.И. Шнейдером. Идеи тезаурусного метода были сформулированы еще основоположником кибернетики Н. Винером. Для понимания и использования информации ее получатель должен обладать определенным запасом знаний.

Если индивидуальный тезаурус потребителя S _П отражает его знания о данном предмете, то количество смысловой информации I _С, содержащейся в некотором сообщении, можно оценить степенью изменения этого тезауруса, произошедшего под воздействием данного сообщения. Очевидно, что количество информации I _С нелинейно зависит от состояния индивидуального тезауруса пользователя, и хотя смысловое содержание сообщения S _П постоянно, пользователи, имеющие различные тезаурусы, будут получать неодинаковое количество информации. В самом деле, если индивидуальный тезаурус получателя информации близок к нулю ( 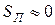), то в этом случае и количество воспринятой информации равно нулю: .

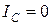Иными словами, получатель не принимает принятого сообщения и, как следствие, для него количество воспринятой информации равно нулю. Такая ситуация эквивалентна прослушиванию сообщения на неизвестном иностранном языке. Несомненно, сообщение не лишено смысла, однако оно непонятно, а значит, не имеет информативности.

Количество семантической информации I _С в сообщении также будет равно нулю, если пользователь информации абсолютно все знает о предмете, т.е. его тезаурус S _П и сообщение не дают ему ничего нового.

Функция зависимости количества информации I _С от состояния индивидуального тезауруса пользователя S _П  приведена на рис. 1.2.

Рис. 1.2. Кривая функции

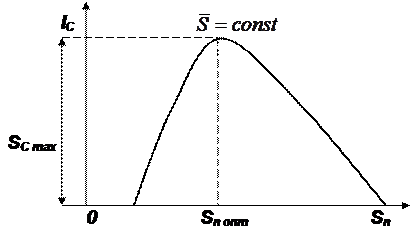
Тезаурусный метод подтверждает тезис о том, что информация обладает свойством относительности и имеет, таким образом, относительную, субъективную ценность. Для того чтобы объективно оценивать научную информацию, появилось понятие общечеловеческого тезауруса, степень изменения которого и определяла бы значительность получаемых человечеством новых знаний.

Прагматический подход определяет количество информации как меры, способствующей достижению поставленной цели. Этот подход базируется на статистической теории Шеннона и рассматривает количество информации как приращение вероятности достижения цели до получения информации, равной P ₀, а после получения P ₁ прагматическое количество информации I _П  определяется как

.

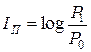Если основание логарифма сделать равным двум, то I _П  будет измеряться в битах, как и при статистическом методе.

При оценке количества информации в семантическом и прагматическом аспектах необходимо учитывать и временную зависимость информации. Дело в том, что информация, особенно в системах управления экономическими объектами, имеет свойство стареть, т.е. ее ценность со временем падает, и важно использовать ее в момент наибольшей ценности.

Структурный подход связан с проблемами хранения, реорганизации и извлечения информации и по мере увеличения объемов накапливаемой в компьютерах информации приобретает все большее значение.

При структурном подходе абстрагируются от субъективности, относительной ценности информации и рассматривают логические и физические структуры организации информации. Но для ее эффективного использования необходимо определить такие структуры организации информации, чтобы существовала возможность быстрого поиска, извлечения записи, модификации информационной базы.

При машинном хранении структурной единицей информации является один байт, содержащий восемь бит (двоичных единиц информации). Менее определенной, но также переводимой в байты является неделимая единица экономической информации – реквизит.

Реквизиты объединяются в показатели, показатели – в записи, записи – в массивы, из массивов создаются комплексы массивов, а из комплексов – информационные базы. Структурная теория позволяет на логическом уровне определить оптимальную структуру информационной базы, которая затем с помощью определенных средств реализуется на физическом уровне – уровне технических устройств хранения информации. От выбранной структуры хранения зависит такой важный параметр, как время доступа к данным, т.е. структура влияет на время записи и считывания информации, а значит, и время создания и реорганизации информационной базы.

Информационная база совместно с системой управления базой данных (СУБД) формирует автоматизированный банк данных.

Значение структурной теории информации растет при переходе от банков данных к банкам знаний, в которых информация подвергается еще более высокой степени структуризации.

После преобразования информации в машинную форму ее аналитический и прагматический аспекты как бы уходят в тень, и дальнейшая обработка информации происходит по "машинным законам", одинаковым для информации любого смыслового содержания. Информация в машинном виде, т.е. в форме электрических, магнитных и тому подобных сигналов и состояний, носит название данных; для того чтобы понять их смысловое содержание, необходимо данные снова преобразовать в информацию (рис. 1.3).

Рис. 1.3. Схема преобразования "информация – данные"

Преобразования "информация – данные" производятся в устройствах ввода-вывода ЭВМ.